同期機のベクトル図へのPU法適用

 

　まず，PU(Per Unit)化とは何だったかを思い出してみよう．PU化とは，PU法の単位に電気量を変換することである．

　例えばある電圧をPU法の単位に変換するときには，\(1\)[p.u]が何ボルトなのかを知る必要がある．もし\(1\)[p.u.]が\(100V\)ならば，\(110V\)は\(1.1\)[p.u.]となる．そしてPU法の特徴としては，\(1\)[p.u.]は場合に応じて変わる（自由に決められる）のである．通常は\(1\)[p.u.]の値はその系の定格値が適用される．つまり，定格電圧\(66\)[kV]の送電線のPU化の際には，\(1\)[p.u.]を\(66\)[kV]として計算するのが一般的である．このような\(1\)[p.u.]の値を基準値と呼ぶ．そしてPU化された後の値は基準値からの倍率そのものを表しているので，例えば\(66\)[kV]の\(0.9\)倍の電圧値は，基準値が\(66\)[kV]ならばPU法で表すと\(0.9\)[p.u.]となる．

　それでは同期機のベクトル図をPU化してみよう．PU化するときには上記の議論からも明らかなとおり，まずは基準値を決める必要がある．ベクトル図というのは1相分の電圧を表していたので，ベクトル図の基準値にふさわしいのは相電圧の定格値であろう．線間電圧の定格値を\(V_n\)とすると，相電圧の定格値は

$$\frac{V_n}{\sqrt{3}} \tag{1}$$

　となる．これがベクトル図のPU化の基準値になる．というわけで，ベクトル図の電気量を[p.u.]に変換するべく，下記の図1のように上記（1）の基準値で割ってやる．

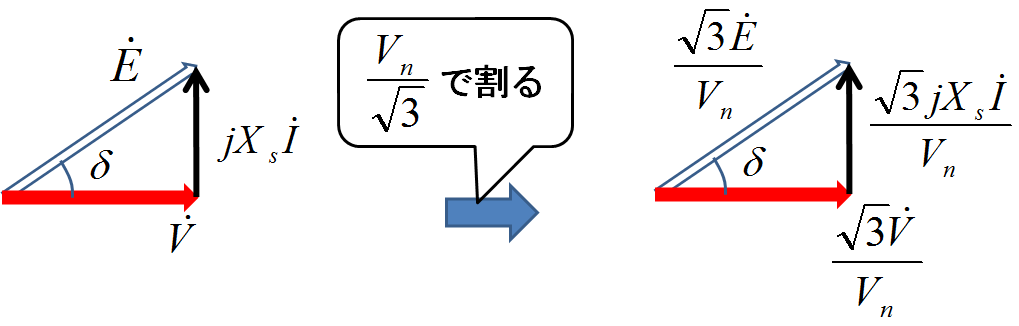
図1.ベクトル図のPU法適用

 

　ここで，PU化された端子電圧\(\dot{\tilde{V}}\)，起電力\(\dot{\tilde{E}}\)，電機子電流\(\dot{\tilde{I}}\)を以下のように定める．

$$\dot{\tilde{V}}\equiv\frac{\sqrt{3}\dot{V}}{V_n},\dot{\tilde{E}}\equiv\frac{\sqrt{3}\dot{E}}{V_n},\dot{\tilde{I}}\equiv\frac{\dot{I}}{I_n} \tag{2}$$

　電圧に関しては相電圧を，電機子電流に関しては定格相電流を，それぞれ基準値においている．これを用いて図1の右側は次の図2のように書き換えることができる．

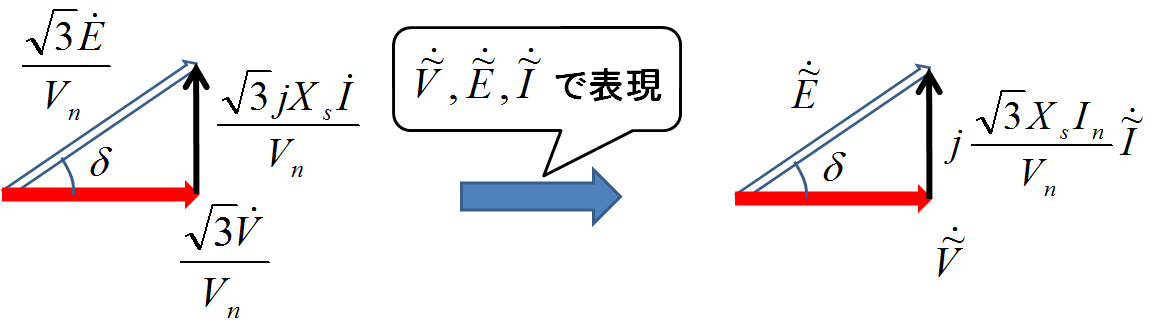
図2.PU法を用いた電気量で表現

 

　これでだいぶベクトル図のPU法適用のゴールは近づいた．唯一同期リアクタンス部分だけがPU法適用前の電気量で表された部分になってしまっていたので，そこも以下のように\(\tilde{X_s}\)とおいてみる．

$$\tilde{X_s}\equiv \frac{\sqrt{3}X_sI_n}{V_n} \tag{3}$$

　この置き換えをすることで，ついにベクトル図は次の図3のように，PU法が適用された電気量のみで表すことができるようになる．

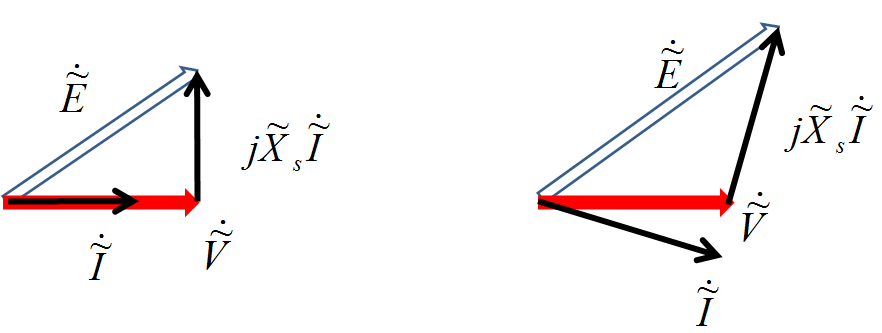
図3.同期リアクタンスもPU法で表現

 

　これでベクトル図のPU化は完了した．PU化された端子電圧\(\dot{\tilde{V}}\)，起電力\(\dot{\tilde{E}}\)，電機子電流\(\dot{\tilde{I}}\)，同期リアクタンス\(\tilde{X_s}\)について，PU化前と完全に同じベクトル図が描ける．そしてこれらのPU化された量は式（2）や式（3）によって求められるのである．PU化の基準値は定格値だったので，このPU化されたベクトル図のベクトル長さが\(1\)ならば，定格に等しく，端子電圧\(\dot{\tilde{V}}\)や起電力\(\dot{\tilde{E}}\)，電機子電流\(\dot{\tilde{I}}\)のベクトルの長さ一般的には\(1\)に近い\(1\)以下の値を取る．そして\(\tilde{X_s}\)の値は水力発電の同期発電機などでは\(0.6\)~\(0.8\)，火力発電の同期発電機などでは\(1\)前後の値を取る．

 

 

 

 

この項の内容に関する，より詳細で完全な解説は，

【徹底解説　電動機・発電機の理論】の§６－１にて展開されています．
是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス