直流機の極数と並列回路数
並列回路数\(a\)というのは,電機子電流\(I\)が\(a\)分割されて各々の電機子導体に流れることを意味している.つまり,下記の図1のように,ブラシを介して供給された電機子電流\(I\)は,各々の導体には\(\frac{I}{a}\)で供給される.
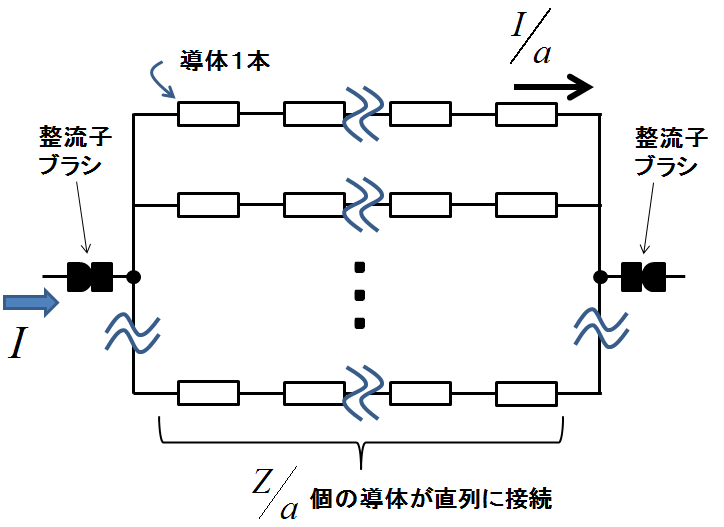
図1.電機子コイルの並列回路数
電動機に大電流を供給できるような状況では,この並列回路数\(a\)をなるべく増やすように設計するのがよいし,逆に電動機に高電圧を供給できるような状況では,この並列回路数\(a\)は最小化してなるべくたくさんの導体を直列に接続してやるのがよい.
それではこの並列回路数\(a\)は,電機子導体同士の接続方法一つでどのような値にもできるのだろうか.その答えを探るため,次の図2のような磁極が2極の場合の直流機を例にとって考えてみる.
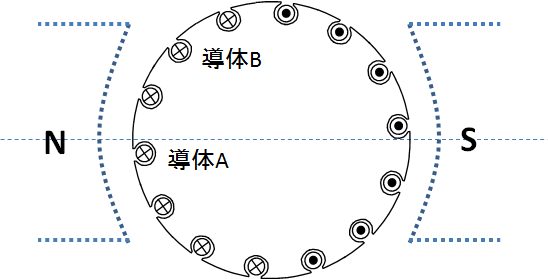
図2.異なる2つの電機子導体(2極の場合)
この図2の導体Aと導体Bは,ともに紙面に対して奥向きの電流を流している.つまり電流方向は同じなので,この2つの導体を並列に接続してみる.すると導体Aと導体Bとで構成される閉ループに大電流の循環電流が流れてしまうのだ.なぜなら導体Aと導体Bは異なる角度に配置されており,当然ながら発生する起電力の位相が異なるので,これらを並列につないでしまうと,その起電力の差から横流が発生してしまうのである.
同様にして考えると,どの異なる導体も異なる起電力を持っているのでそれぞれを並列に接続することはできない.ということで図2に示した電機子コイルの並列数はむやみに増やすことはできず,実際の並列回路数は2となる.
それでは次に,図3のように極数が変わると,この並列回路数の上限に変化が起こるだろうか.
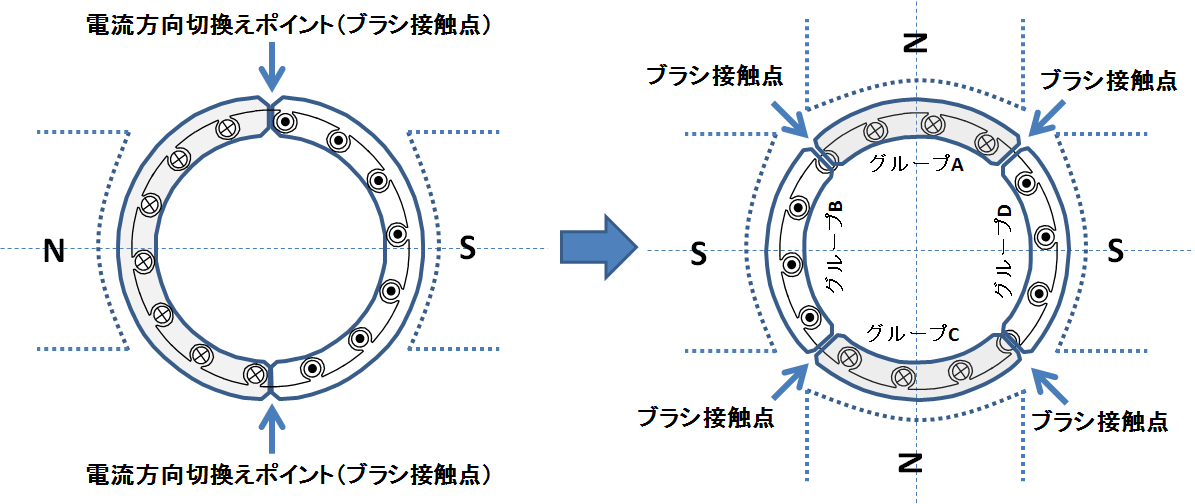
図3.2極の場合(左)と4極の場合(右)
極数が増えれば,それに比例して並列にできる回路数も増えることを図3を見ながら説明しよう.図3の左側は2極の場合,右側は4極の場合を表しており,2極の場合は電機子導体をその電流方向に従って2つにグループ分けし,4極の場合は電機子導体を同様にして4つにグループ分けする.なぜこんな図を作ったのか?それは並列にできる導体部分を明確化するためである.結論から言えば,極数に比例して並列にできる回路数は増える.なぜならば,例えば図3の右側におけるグループBの導体の合計起電力とグループDの導体の合計起電力は釣り合う.またグループAとグループCについても,合計起電力は同じである.よって同図左側のような2極構成のときに比べ,2倍の並列化が可能になったことがわかるだろう.
同様にして,磁極の極数を増やしていけば,それに比例して電機子導体のグループ数も増え,そのグループ間では並列化が可能となるので,確かに極数と並列回路数の最大値は比例しそうである.次の図4は,並列回路数を最大化するような巻き方である重ね巻における,ブラシ接触点位置と並列回路数の様子を表している.
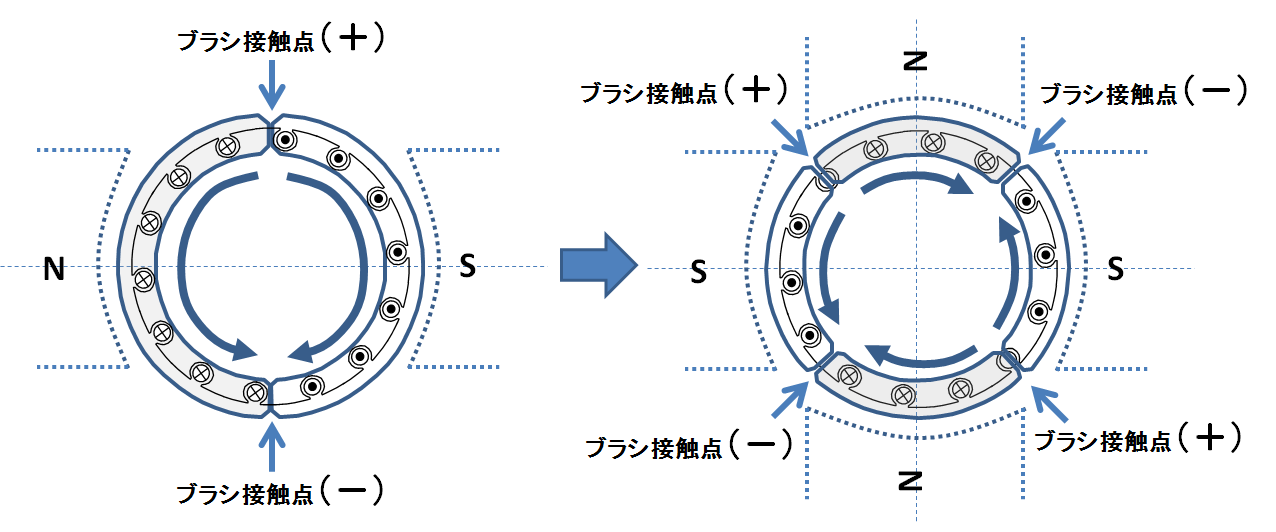
図4.極数と並列回路数の関係(重ね巻)
この図4を見れば明らかなように,極数\(p\)に比例してブラシ接触点も増える.そしてブラシ接触点の数に比例して並列回路数\(a\)も増えている.これが重ね巻のイメージである.巻き方の詳細は次の記事をチェックしていただきたいが,この重ね巻において極数\(p\)と\(a\)の関係を示すと以下のようになる.
$$ a=p \tag{1} $$また,逆に並列回路数をなるべく増やしたくないケース(高電圧で駆動したいケース)では,波巻という巻き方を採用する.これは磁極の極数が増えてもうまいこと電機子導体同士を一筆書きのように直列に結ぶことで,常に並列回路数を2にできるという方式である.よって波巻の際の極数\(p\)と\(a\)の関係を示すと以下のようになる.
$$ a=2 \tag{2} $$
この重ね巻,波巻の詳細は次の記事で説明する.
この項の内容に関する,より詳細で完全な解説は,【徹底解説 電動機・発電機の理論】の§3-2後半にて展開されています.
是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











