同期機のベクトル図と等価回路
“同期機のベクトル図導入”の式(6)から,同期電動機の基本式は以下のようになることがわかった.
ここで,\(\dot{V}\)は端子電圧,\(\dot{E}\)は起電力,\(\dot{I}\)は電機子電流,\(X_s\)は同期リアクタンスである.この式によると,同期電動機の等価回路は以下のように表されることがわかる.
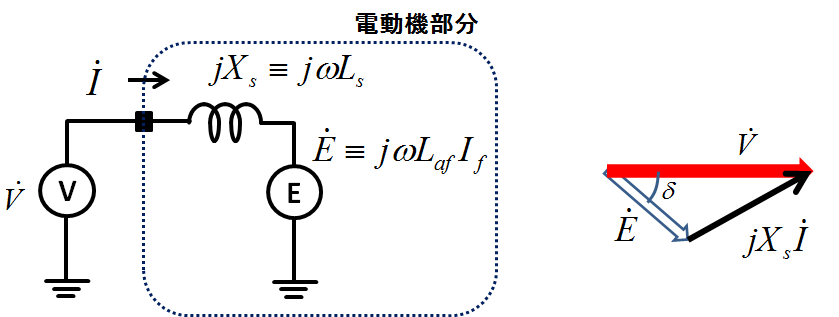
図1.同期電動機の等価回路(左)とベクトル図(右)
図1の点線で囲んだ部分が同期電動機部分である.端子電圧\(\dot{V}\)はこのケースでは電圧源になっている.これは,この電動機が相電圧\(\dot{V}\)の理想的な交流電源によって駆動されていることを意味している.そしてこの等価回路の電圧についての関係式は,上記の式(1)に示した同期電動機の基本式に等しくなることがわかるだろう.等価回路のインダクタンス部分の電圧降下が\(jX_s\dot{I}\)(式(1)の右辺第1項)になることからも明らかである.
次に,同期発電機の基本式と等価回路を考えてみよう.同期電動機と同期発電機では,物理的に起こっていることは全く同一なので,等価回路も全く同じ形になることが予想される.両者の扱いにおいて唯一異なるのは電機子電流\(\dot{I}\)の符号の定義である.発電機の場合,式(1)は以下のような変更を受ける.
式(1)と式(2)は純粋に電機子電流\(\dot{I}\)の符号の差だけであることはおわかり頂けるだろう.この式を満たすような等価回路は,次の図2となる.
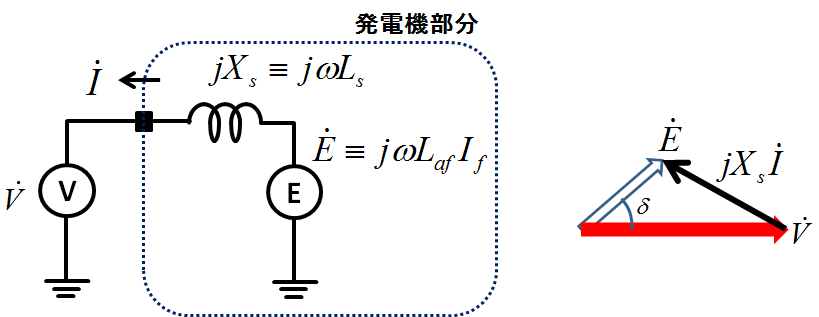
図2.同期発電機の等価回路(左)とベクトル図(右)
図1とは電機子電流の矢印が反対になっているだけで,等価回路本体は全く同じである.この等価回路の電圧に関する式がちょうど式(2)と一致することも自明であろう.ということで同期電動機・発電機についての等価回路がそれぞれ図1,図2のようになることが示された.
最後に,等価回路に寄生抵抗の効果を入れてみよう.図3をご覧いただきたい.
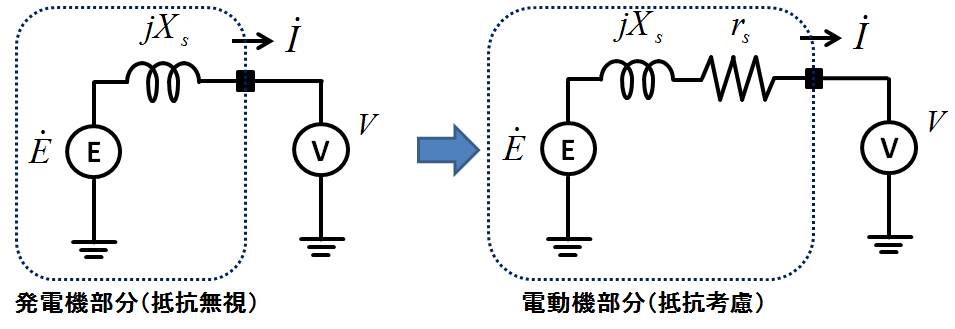
図3.寄生抵抗と等価回路
発電所などの大型同期発電機などにおいては電機子コイルの寄生抵抗は無視できるので図3の左側の等価回路で十分なのだが,実際には若干の寄生抵抗が存在するので,その効果を考慮に入れると図3の右側のような等価回路となる.\(r_s+jX_s\)は同期インピーダンスと呼ぶ.
では実際に,上記の図3を用いて電機子電流を求めることを考えてみよう.この等価回路だけで電流を求めることは可能だろうか?答えは残念ながらNoである.なぜならば,端子電圧と起電力との間の位相差(負荷角)がどうなるのかがわからなければ電機子電流は求められないからである.そして負荷角は上記の図3単独で導き出せるものではなく,機械的入出力の大きさを考慮にいれなければならない.具体的には,こちらの式を用いて,これに機械的入出力の値を入れて負荷角を割り出すことが必要である.ただ,ひとたび負荷角がわかれば起電力の位相が特定できるので,あとは上記の図3ないしはベクトル図を用いて電機子電流を計算できる.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】のP.160~P.172にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











