直流機のトルクと起電力まとめ

 

　最後に直流機のトルクと起電力のまとめをしておこう（このページは直流機のトルクと，直流機の起電力の２つの記事のまとめである）．

　これまでの2つの記事において，もっとも単純な整流子型直流機（図1）を題材にトルクと起電力の計算をしてきたが，2つの計算の間には類似点がいくつもあったので，ここで一緒にまとめておきたい．図1の例でトルクと起電力を求めると，いずれも電機子コイルの回転位置\(\theta\)の関数となり，ともに図2に示すような，\(\cos\)関数の絶対値を取った形になることがわかっただろう．

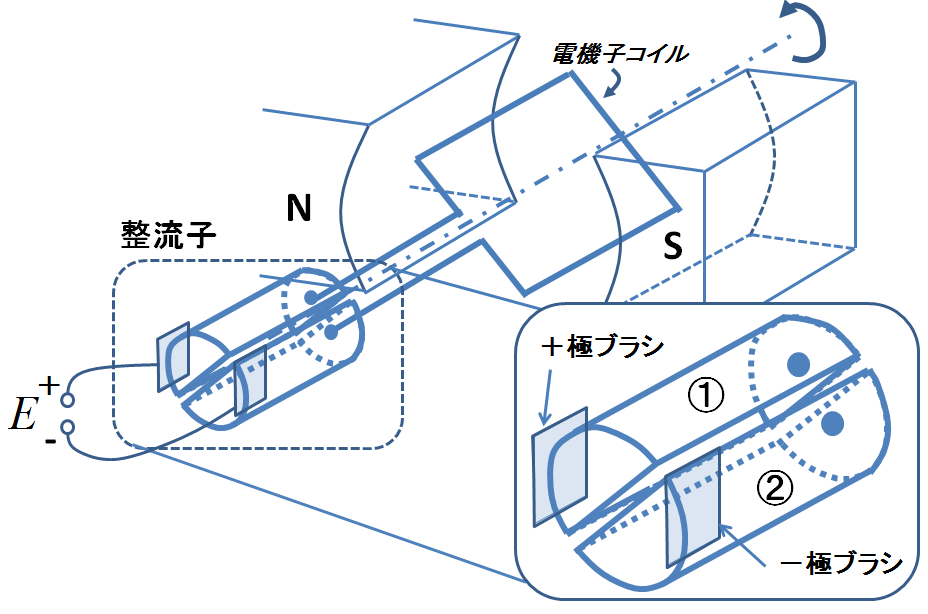
図1.整流子型直流機

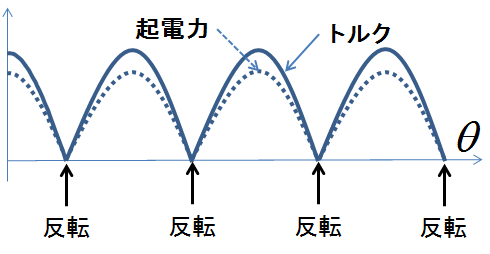
図2.直流機のトルクと起電力


 

　まずこの図2を見ると，トルクと誘導起電力が完全に比例関係にあることが見て取れる．この比例関係は電機子コイルに流れる電流が時間に対して一定であるという前提が入るが，少なくともこの2つの間には強い関係があることが予想できるだろう．現にこのあとすぐに（式（3）において）それははっきりすることとなる．

　とりあえず直流機のトルクの式（3）と直流機の起電力の式（3）を下記に改めて並べてみる．

$$T=2RF_{||}=2RIBL\left | \cos\theta \right | \tag{1}$$ $$E=2\omega BLR\left | \cos\theta \right | \tag{2}$$

　この式（1）と式（2）はよく似ている．電流\(I\)と角速度\(\omega\)以外，両者は完全に共通であることがわかるだろう．ということは，次の関係を満たすこともすぐにわかる．

$$\omega T=IE \tag{3}$$

　この式（3）の左辺は，機械的出力（発電動作時は機械的入力）と等しく，右辺は消費電力（発電動作時は発生電力）と等しいので，この式は，「機械的出力（入力）と消費（発電）電力は常に釣り合っている」という物理的な特性を表している．損失を無視すれば，電力と機械的な仕事は常に釣り合っているのだ．

　ところでこれはある回転位置\(\theta\)における瞬間的なトルク・起電力だったので，回転している実際の直流機における導体1本分のトルク・起電力への寄与を求めるためには，その時間平均をとる必要がある．つまり，下記の\(\overline{T}\)や\(\overline{E}\)のような平均値を計算する必要があるだろう．

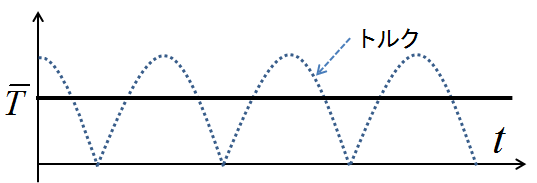
図3.整流子型直流機

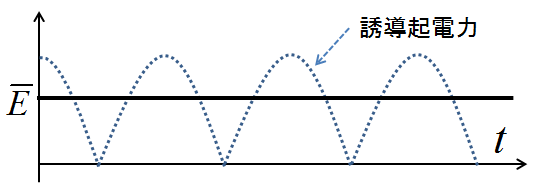
図4.直流機のトルクと起電力


 

　この平均値の計算過程は，リンク（トルクと起電力）を参照していただくとわかるが，電流が流れる導体1本当たりのトルクの寄与\(\overline{T_1}\)と起電力の寄与\(\overline{E_1}\)は下記のように求まる．

$$\overline{T_1}=\frac{I\Phi}{\pi} \tag{4}$$ $$\overline{E_1}=\frac{\omega\Phi}{\pi} \tag{5}$$

　ここで\(\Phi\)は1極当たりの磁束を表しており，この結果は図1のもの（2極の場合のもの）である．そもそもトルクや起電力を時間について平均化した定数として扱っていい最大の理由は，以下の図10のようなイメージで説明できた．

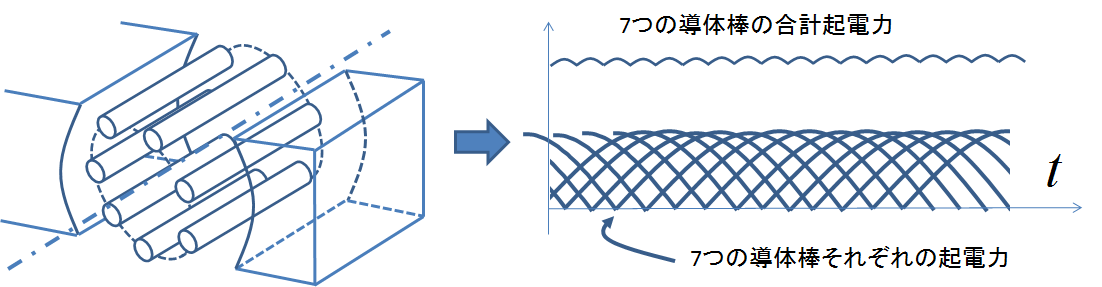
図5.分布的に導体数が増えた直流機の誘導起電力

 

　このように分布的に導体の本数が増えた場合は，少しずつ位相のずれたトルク（起電力）を足し合わせることで全体としてトルク（起電力）変動が少ない直流機を構成することができる．例えばこの図10の起電力について考えると，分布的に等間隔で設置された導線同士が直列に結ばれ，直流機全体としての起電力は各導体に発生した起電力の和となり，各導体の起電力変動はほぼ相殺しあう．実際ほぼすべての実用例において，このような分布的なコイルの巻き方を採用しており，トルクや起電力は時間に対してほぼ一定となり，余分な振動成分は極力抑えられた設計になっているのである．

　ところで，上記の式(4)や式(5)は図1という非常に単純化された状況における結果だったので，これを実際の例にまで拡張しなければ使い物にはならないことは明らかだろう． 具体的には並列回路数\(a\)や総導体数\(Z\)，極数\(p\)の情報から，その直流機全体のトルクと誘導起電力の式を導かねばならない．

　詳細の計算は書籍に譲るとして，ここでは結果のみ示すことにしよう．

$$T=\frac{pZ}{2\pi a}I_a\Phi = k_2I_a\Phi \tag{6}$$ $$E=\frac{pZ}{2\pi a}\omega\Phi =kn\Phi \tag{7}$$

　ただし，\(k_2\)と\(k\)は以下の通り．

$$k_2=\frac{pZ}{2\pi a} \tag{8}$$ $$k=\frac{pZ}{a} \tag{9}$$

　直流機のトルクと誘導起電力の基本的な解説は以上となる．次はこれを用いて，直流電動機のトルク特性曲線や速度特性曲線がどのように求められるのかについて考えてみよう．

 

 

 

この項の内容に関する，より詳細で完全な解説は，【徹底解説　電動機・発電機の理論】のP.91～P.94にて展開されています．
是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス