同期調相機について
今回は同期調相機について,その働きと物理的な原理について説明していくことにしよう.まず下記の図1は同期調相機の機能を簡単に絵にしてみたものである.
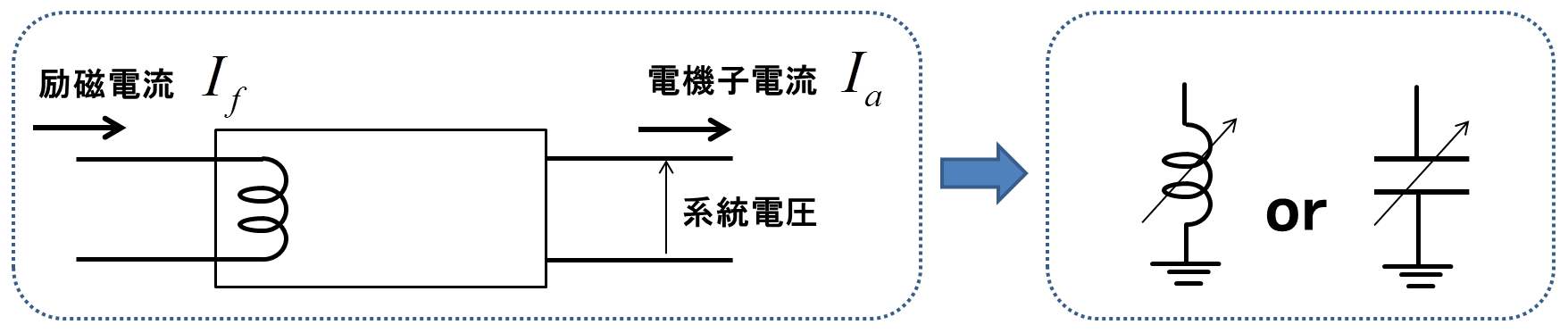
図1.同期調相機の機能
図1を見れば明らかなように,同期調相機というのは可変キャパシタ(ないしは可変インダクタ)とみなせる.そして励磁電流\(I_{f}\)を変えることでキャパシタンス(ないしはインダクタンス)を変化させることができるのである.このような機能は,機械的負荷が0で空回りしている同期機によって達成されるので次にその原理を説明していこう.
下記の図2は,機械的負荷があるときと無いときの同期機の様子を示している.
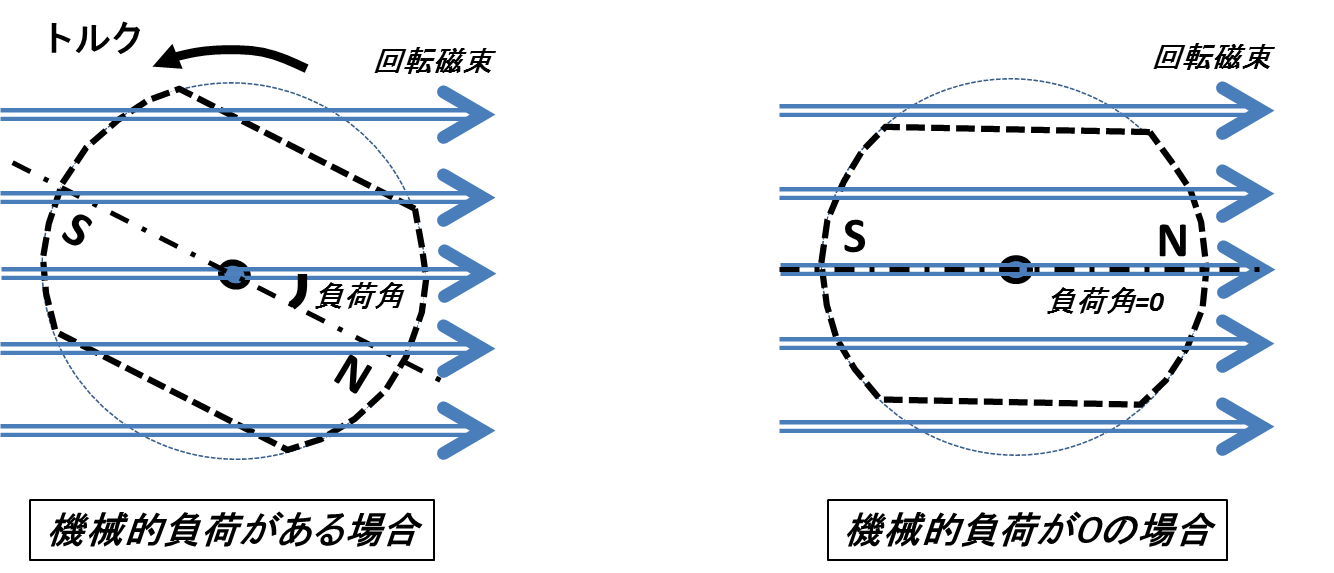
図2.機械的負荷がある場合(左)とない場合(右)
同期調相機というのはこの図2の右側の状態に当たる.これは無負荷により空回りしている状況なので,負荷角が0,つまり回転磁束と回転磁極の向きが一致している状態である.この状態がなぜ可変キャパシタ・インダクタになるのだろうか?その答えを知るため,まずは負荷角0の同期機の回転磁束がどうなっているのか調べてみる.
下の図3は負荷角が0のときの回転磁束の内訳を示している.
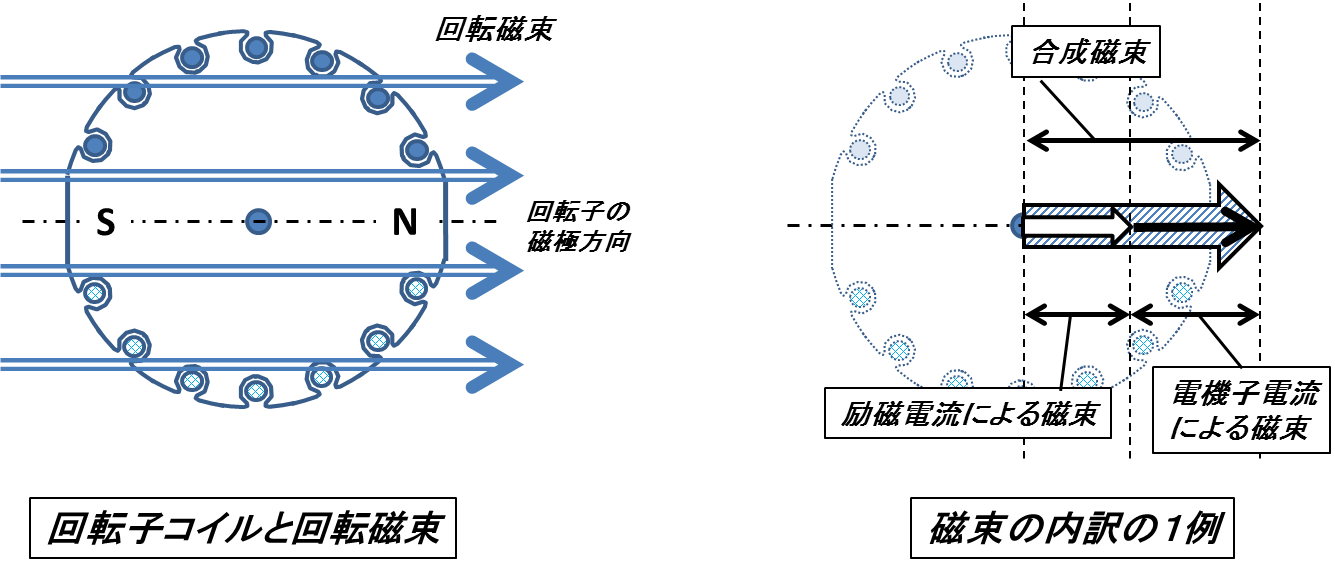
図3.機械的負荷がない場合の回転磁束の内訳
これを見れば明らかなように,電機子電流による磁束と励磁電流による磁束は互いに一直線上であり,この2つの合成が回転磁束になっているのである.そして回転磁束の強さは端子電圧により決定されるので,一定電圧の母線に連系された同期機の場合この回転磁束は一定となる.この場合どうなるかというと,励磁電流を増やせば電機子電流は減っていき,励磁電流がある量になったときに電機子電流は0になり,そこからさらに励磁電流を流すと今度は電機子電流の位相が反転し増加に転じることとなる.これはすべて,両者の磁束の合成である回転磁束が一定となる物理法則(ファラデーの法則)により,励磁電流による磁束変化は電機子電流の変化により打ち消されるのである.次の図4において,今の話をベクトル図に落とし込んでみよう.
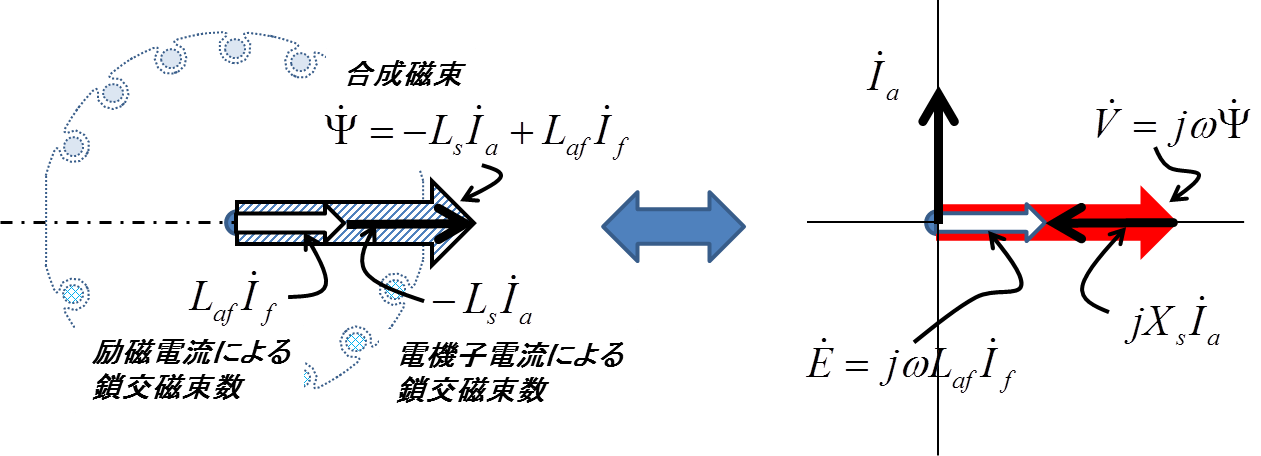
図4.同期調相機のベクトル図
電機子コイルの抵抗を無視すれば,回転磁束が一定というのは端子電圧が一定(無限大母線に連系している)ということと等価である.つまり同図右側のベクトル図で言えば,赤い矢印の長さ\(V\)が一定となっている.ここで白の矢印で示した起電力 \(\dot{E}\)が励磁電流\(I_{f}\)を変えることで伸び縮みするので,その差分の黒い矢印\(jX_{s}\dot{I}_{a}\)の長さも必然的に伸び縮みする. そして\(jX_{s}\dot{I}_{a}\)は実軸上となるので,電機子電流\(\dot{I}_{a}\)は純虚数となることもわかるだろう.これはまさに有効電力0で無効電流の大きさが励磁電流\(I_{f}\)により調整できることを示している.
回転磁束とベクトル図の対応がよくわからなかった方は”同期機のベクトル図導入”を復習いただきたい.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】のP.184~P.187にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











