誘導加熱と誘電加熱
この項では誘導加熱と誘電加熱について説明していきたい.名前は似ているものの,加熱の原理は大きく異なるので注意されたい.次の図1で両者の違いを明確にしておく.
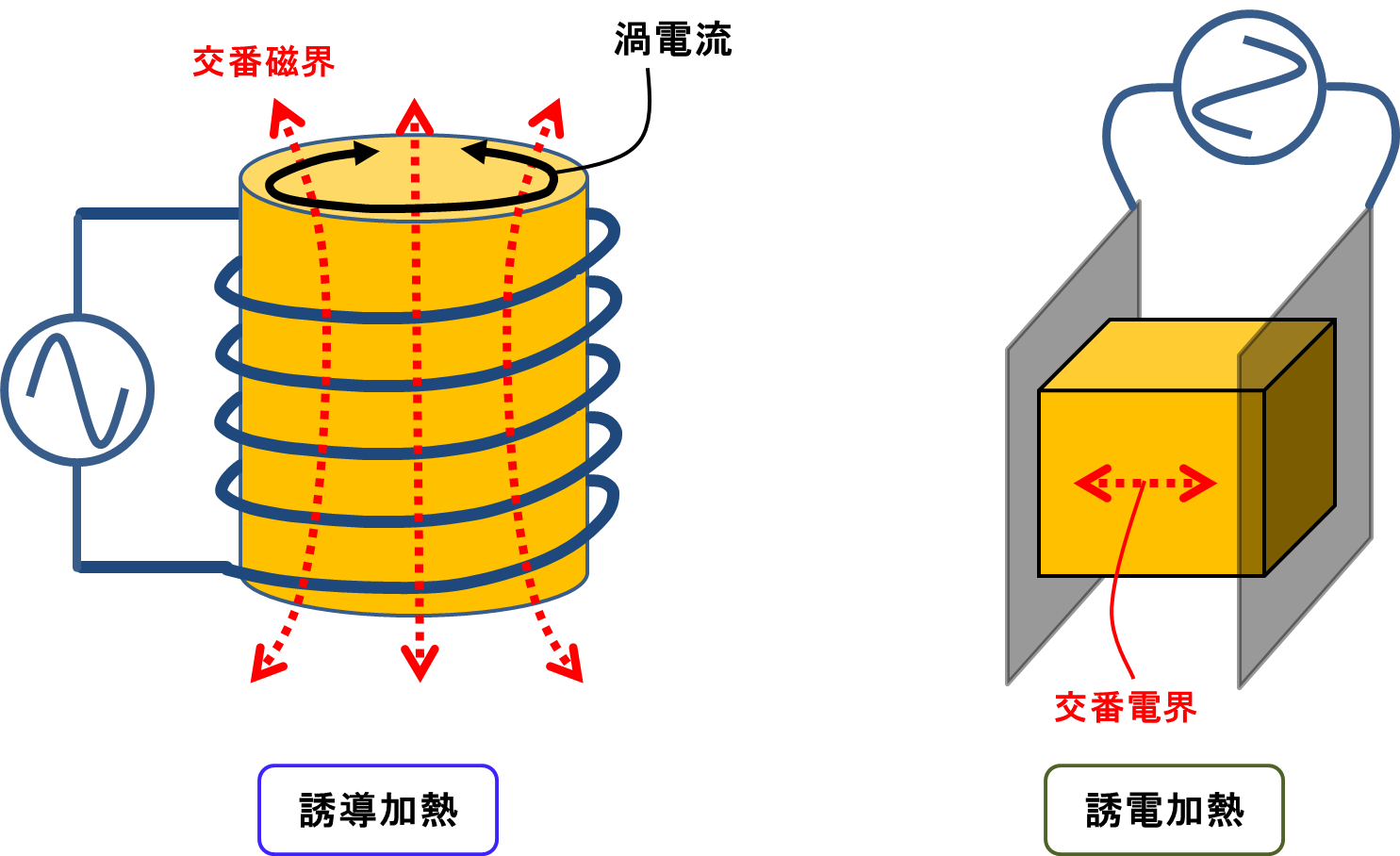
図1.誘導加熱と誘電加熱の比較
図1の左側が誘導加熱,右側が誘電加熱である.誘導加熱は交番磁界を,誘電加熱は交番電界を加熱対象に与えることにより加熱対象自体を発熱体として加熱する方式である.簡単に両者の比較を下記の表1で記した.
$$ 表1.誘導加熱と誘電加熱の比較\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|c|c|c|} \hline \T & \ \ \ 誘導加熱\ \ \ & \ \ \ 誘電加熱\ \ \ \\\hline \ 加熱対象\ & 電気伝導体 & 誘電体 \\ 印加する場 & 交番磁界 & 交番電界 \\ 発熱要因 & 渦電流のジュール熱 & 誘電損失 \\ 使用周波数 & 数十Hz~数十MHz & 1MHz~数百MHz \\\hline \end{array} $$
まずは誘導加熱から説明していこう.
誘導加熱
誘導加熱は,図1の左側に示した通り,コイルに交流電流を流すことで交番磁界を発生させ,それを電気伝導体に印加することで渦電流を発生させて,そのジュール熱により伝導体自身を加熱するという,非接触型の加熱方式である.改めて代表的な形の誘導加熱方式を次の図2に示そう.

図2.誘導加熱と周波数
内部の渦電流によるジュール熱ということで物体の内部からの発熱ができるので,高効率で迅速な加熱が可能であり,表面におけるスケールの発生なども抑えてくれる.また,周波数を変えることによって表面からどのくらいの深さまで加熱するかもコントロールできる.周波数を高めると表皮効果により渦電流が表面に集中し,図2の右側のように表面付近のみが発熱するようになる.円筒形の伝導体において表皮の深さ\(\lambda\)とすると,
ただし,\(\sigma\)は電気伝導率,\(\mu\)は透磁率,\(\omega\)は交流の角周波数である.周波数が高いほど,表皮深さは浅くなることがわかるだろう.
次にこの誘導加熱が,電気的にはどのような等価回路で表されるのか,次の図3に示した.

図3.誘導加熱の等価回路
変圧器と同じである.コイルで磁場を起こし,その磁場で2次側(つまり加熱対象)に電流を誘起するというのはやっていることは変圧器そのものであり,等価回路も図3のように変圧器の2次側でのジュール熱の消費として表現される.
それではなぜ通常の変圧器では鉄心が赤熱しないのだろうか?それは変圧器の鉄心内では渦電流が大きくならぬよう,0.2~0.3mm程の非常に薄い鋼板を絶縁物を介しながら積層させたものを用いているからである.
次に同じく交流を用いる加熱方法として誘電加熱について解説していこう.
誘電加熱
誘電加熱というのは,誘導加熱とは違い,電気伝導体ではなく絶縁体(誘電体)を加熱するための手法である.誘電体に印加するのは高周波の電場(電磁場)となる.高周波の電場で誘電体が加熱されるイメージを次の図4に示す.

図4.高周波の電場を印加された誘電体
誘電体というのは,プラスに帯電した原子とマイナスに帯電した原子が規則正しく結合された結晶であり,ここに高周波の電界がかかるとプラスの原子とマイナスの原子が逆方向に動き,格子構造が周期的に変位を起こす.簡単に言うと格子の構造が揺さぶられることになる.もちろん結晶構造の誘電体でなくても分子に分極(プラスとマイナスの帯電の偏り)があれば,誘電加熱は可能である.
ここからは結晶構造の誘電体に話を絞って誘電加熱の原理を探っていく(結晶構造でなくとも電気分極できる分子構造なら同様の説明が成り立つ).次の図5は誘電損失のイメージを示している.
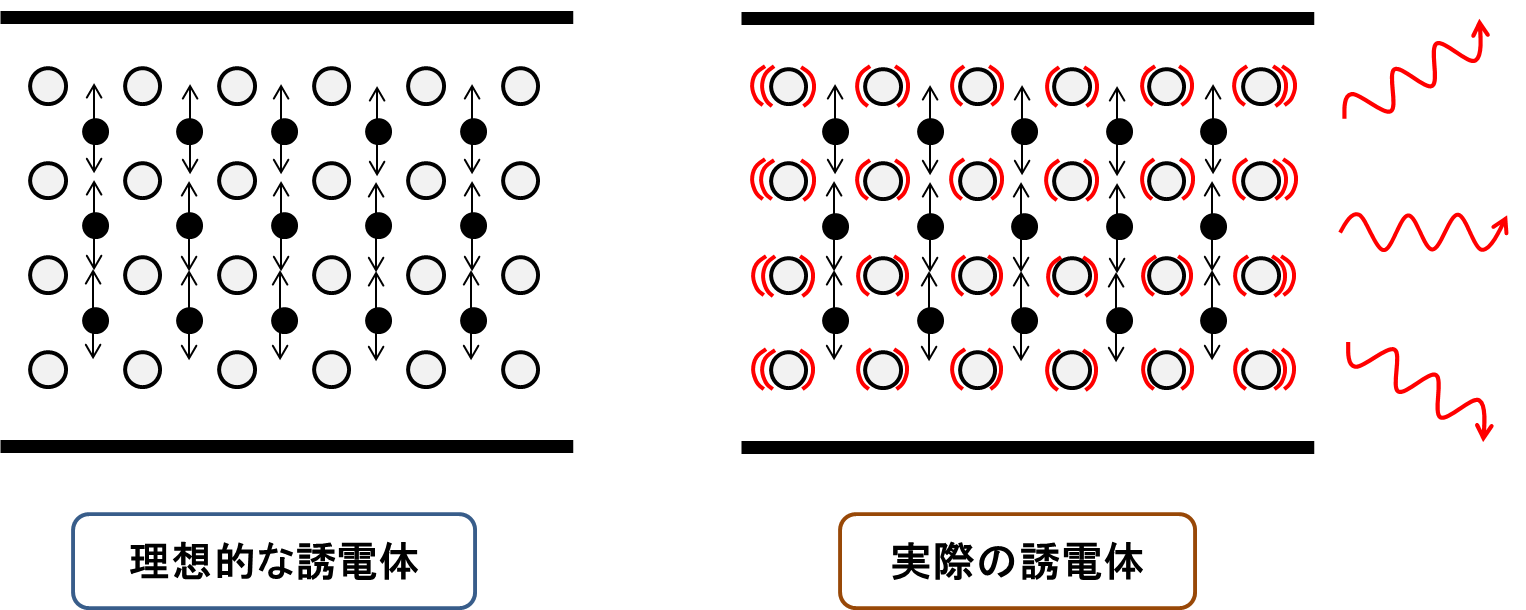
図5.理想的な誘電体と実際の誘電体
誘電損失がある誘電体では,分極(プラスとマイナスの相対位置が変位)をするたびに,格子の振動に起因する損失が発生し,発熱する.これがあって初めて誘電加熱が成立する.
もうちょっと詳しくこの分極における誘電損失のイメージを説明してみよう.
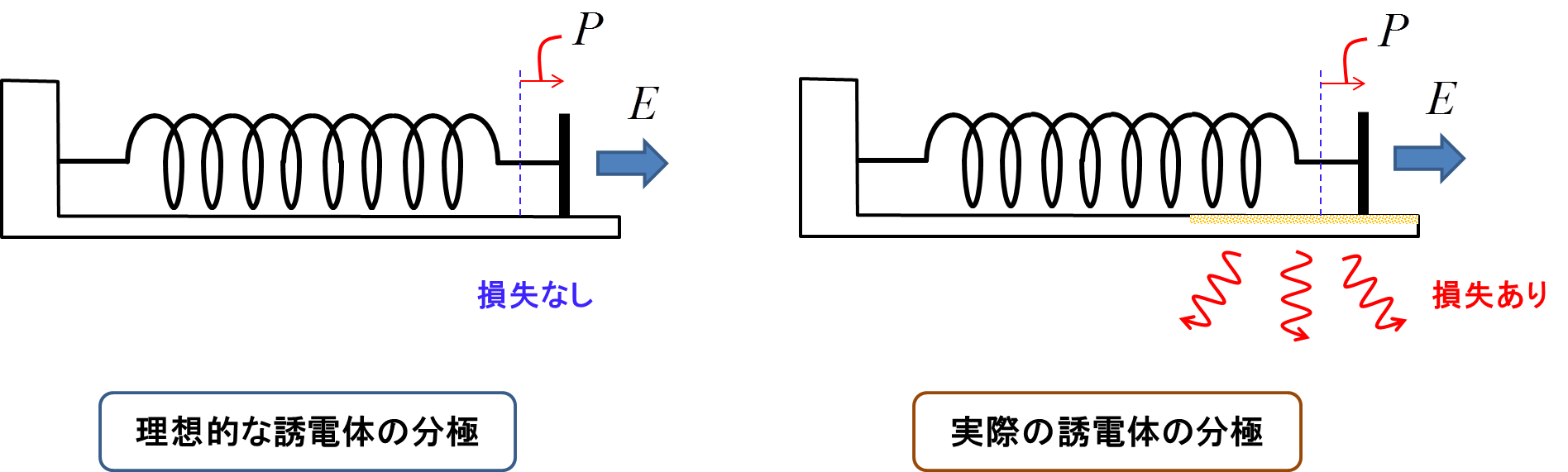
図6.理想的な分極と損失ありの分極
電気分極は印加された電界に比例する.それはバネにおけるフックの法則とアナロジーがある.バネはエネルギーを蓄えるだけで消費はしない.理想的な誘電体でも分極は弾性的でエネルギーは消費されない.ところが実際の誘電体では分極のたびにそのエネルギーの一部が格子振動のエネルギーに変換されてしまう.それは,バネのモデルに対応させると,バネが床と摩擦を起こしているようなイメージとなる.
このイメージを踏まえて,電界\(E\)と誘電分極\(P\)の時間変化を,理想と実際の誘電体において比較してみる.
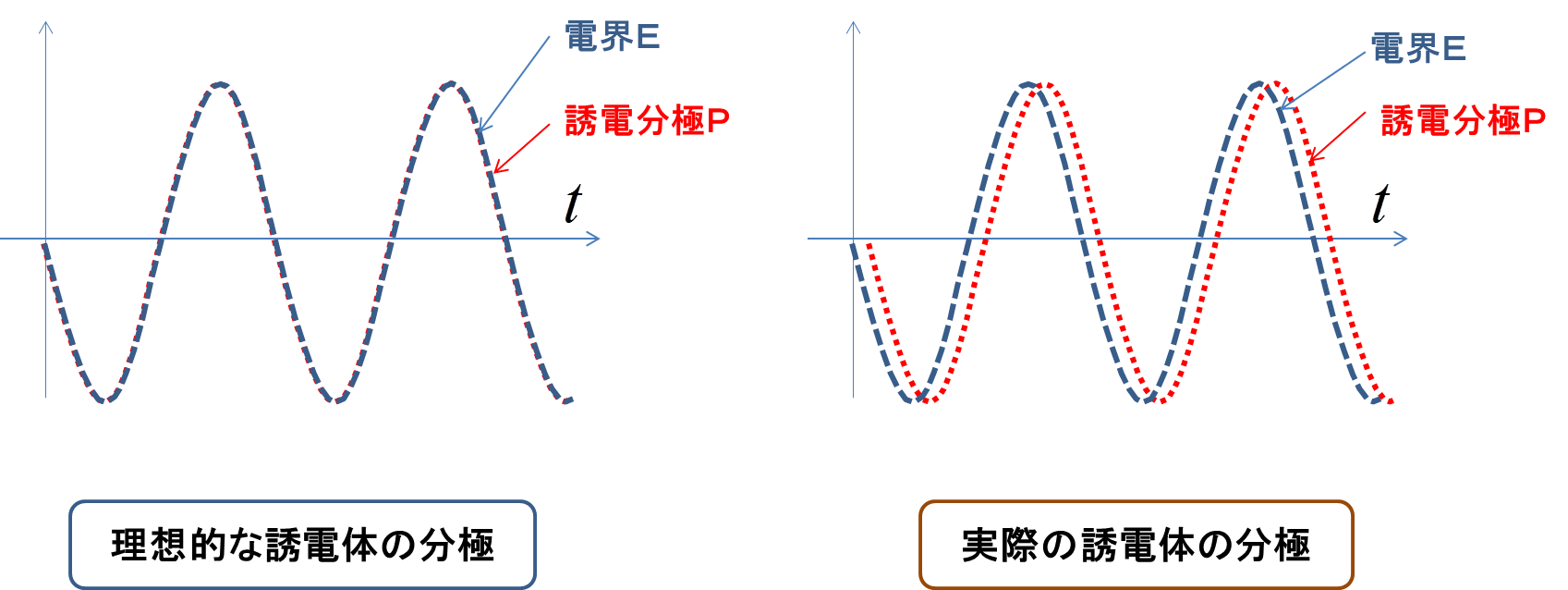
図7.理想的な分極と損失ありの分極の時間変化
摩擦ありの振動系は,外力に対して位相が遅れる.つまり電界\(E\)に対して分極\(P\)が若干遅れる.分極\(P\)を時間微分するとそのキャパシタに流れる電流(のうちの誘電体による成分)となるので,電流のフェザー表示も実際の誘電体の場合には位相が若干遅れる.次の図8に示した.
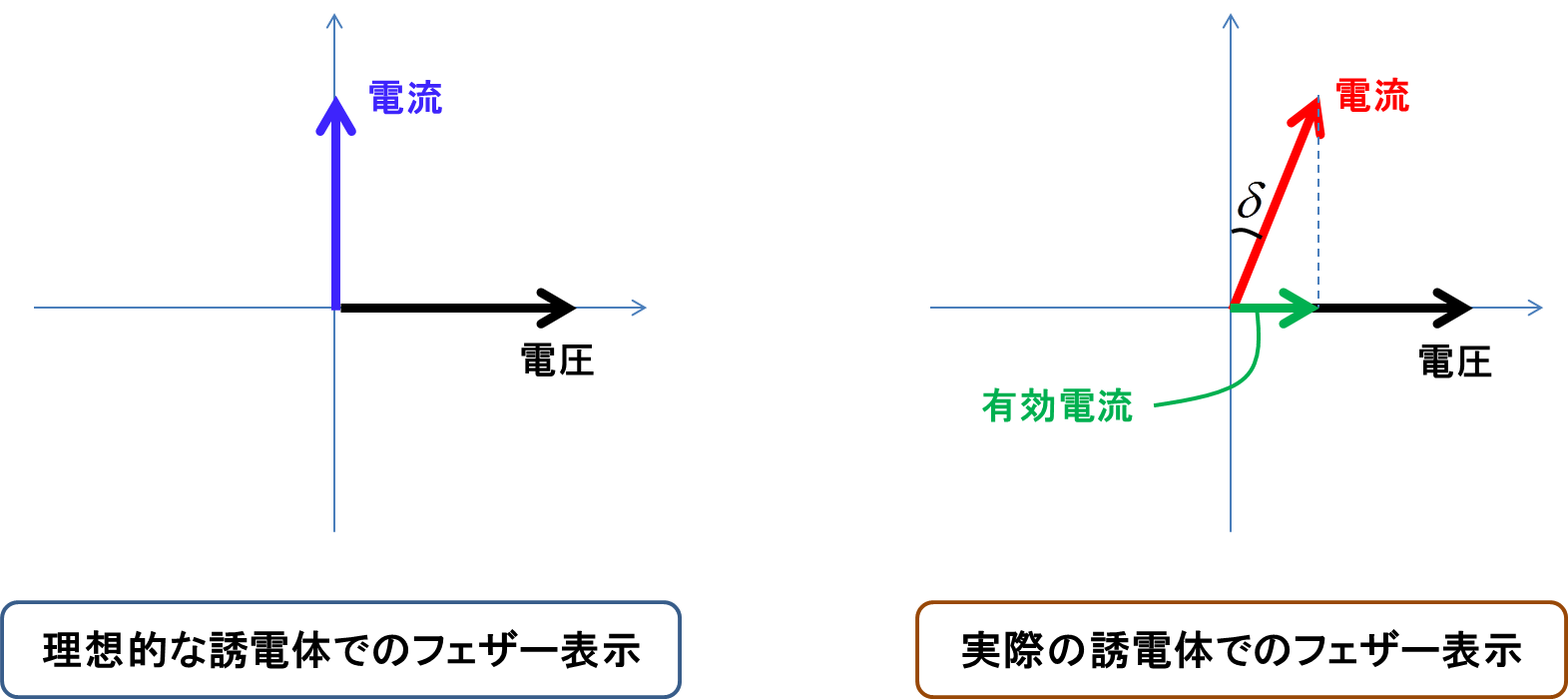
図8.印加した高周波電圧と流れる高周波電流の位相関係
図8によると理想的な誘電体で構成されたキャパシタには無効電流のみ流れるが,実際の誘電体においては電流の位相が\(\delta\)だけ遅れるので,有効電流が発生し電力消費が起こる.
これは等価回路に落とし込むと,下記のようになる.

図9.誘電加熱の等価回路
誘電体が理想的なら当然キャパシタのみでモデル化されるが,誘電体の変位電流が理想(100%無効電流)から\(\delta [rad]\)だけずれるので,その分平行に抵抗\(R\)が出現する.\(C\)に流れる電流の実効値を\(I_{C}\),\(R\)に流れる電流の実効値を\(I_{R}\)とすると,
となり,有効電流\(I_{R}\)の大きさを見積もる上で\(\tan{\delta}\)の値が重要になることがわかる.これをタンデルタと呼ぶ.このタンデルタは高周波になればなるほど,大きくなる.つまり誘電損失を上げたいと思ったら,このタンデルタを上げるべく,高周波を印加する必要がある.
以上で誘導加熱,誘電加熱の説明を終了する.どちらも比較的高周波を用いるため,無線機器などへの影響,また周辺治具への誘導電流などへの影響を考慮した設計を考える必要がある.
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











