誘導機の電磁気学的解説
誘導電動機のざっくりした回転原理は前回の記事”誘導電動機の回転原理”で説明したが,今回はもう少し掘り下げて,誘導機(誘導電動機・誘導発電機ともに成り立つ)の動作時に磁場や誘導電流などがどのように生じていて,それがトルクなどの特性にどのような影響を与えているのか,直感的に観察していくことにしよう.
まず下記の図1を見ていただきたい.これはかご形誘導機の構造を表した概略図である.
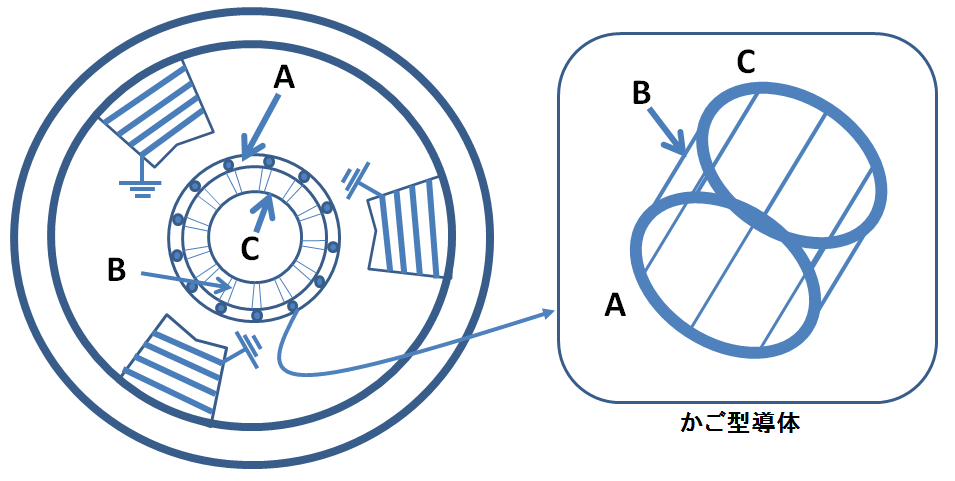
図1.かご形誘導機の構造
この図1は,3つのコイルで示した固定子コイルがかご形導体に回転磁界を与え,まさにかごの形をした導体が回転力を受けるという構造を示している.
その回転磁界とかごの回転の様子を示したものが次の図2になる.
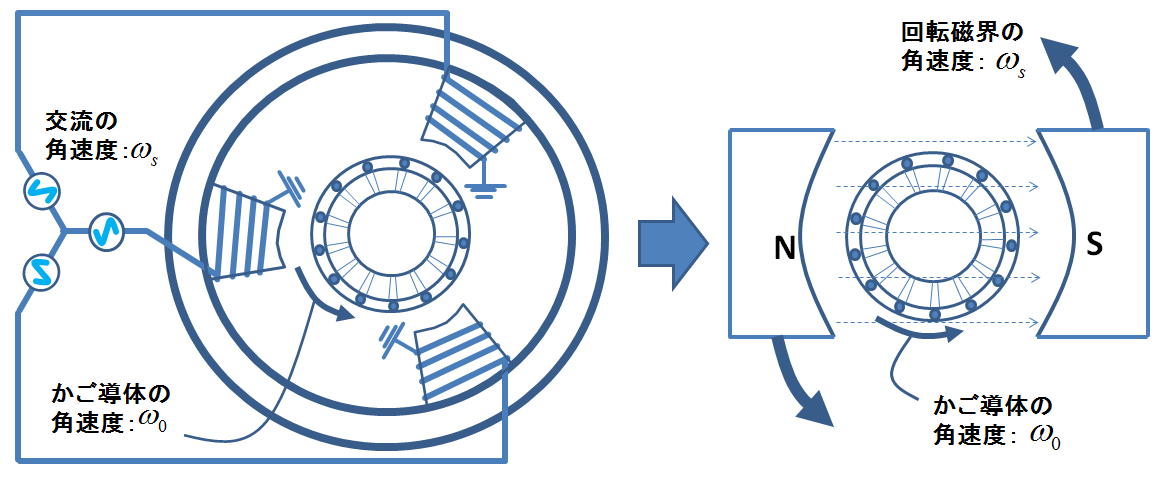
図2.誘導機の2つの角速度
この図2の想定では,かご形導体も回転磁界も紙面に対して反時計回りで回っているとしている(回転機を数学的に記述するときは反時計回りがスタンダードである).そして,三相交流の角速度を\(\omega_{s}\)とすると,この場合極数は2なので回転磁界の角速度も\(\omega_{s}\)となる.(極数が\(p\)ならば回転磁界の角速度は\(\frac{2\omega_{s}}{p}\)となる.)また,かご形導体の回転角速度を\(\omega_{0}\)とする.誘導機は”すべり”があるので,\(\omega_{s}\)と\(\omega_{0}\)が違う値になる.これは同期機とは決定的に違う点であろう.
回転磁界とかご形導体が両方回ってしまっていては誘導電流などの解析がしにくいので,次の図3に示すように回転磁界から見た視点に切り替えよう.
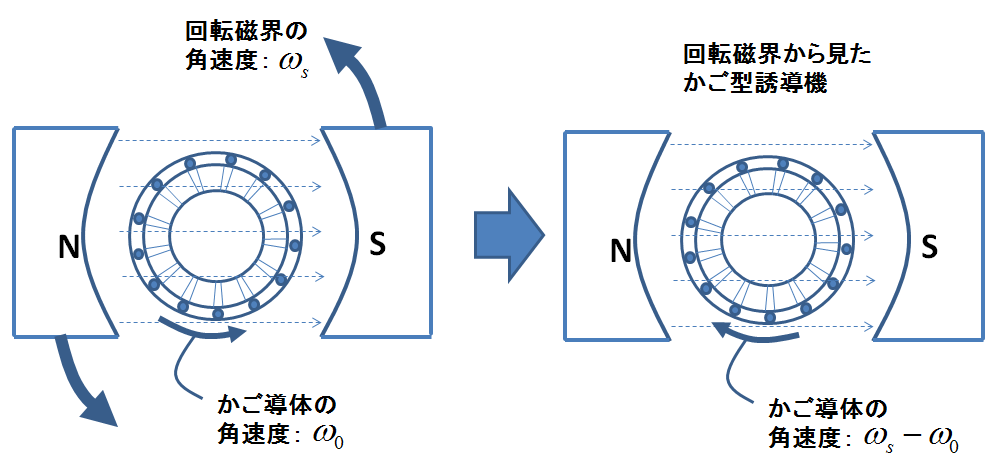
図3.回転磁界から見たかご形誘導機
この図3の右側の視点では,せわしなく回転していたはずの回転磁界は静止磁界となり,かご形導体は2つの相対角速度である\(\omega_{0}-\omega_{s}\)で回転する.ここで電動機であるとすると\(\omega_{s}>\omega_{0}\)なので,かご形導体は回転磁界から見て時計回りに\(\omega_{s}-\omega_{0}\)で回転しているように見える.
このように回転磁界を基準に考えると,静止磁界中を導体がグルグル回っている図に帰着できる.これは電磁気学的には直流機と等価な状況である.ということで直流機のトルクの計算において行ったように,トルクに関わる導体部分を図4のように抜き出してみよう.
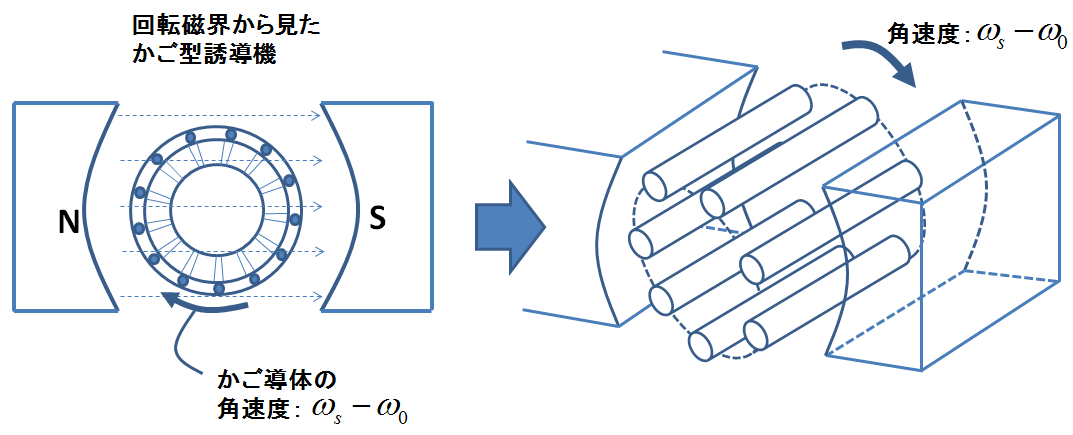
図4.トルクに関与する導体部分の抜出し
直流機のときと同様,トルクに関わる導体部分は回転軸と平行な導体棒の部分である.つまり,この導体棒に流れる電流の分布がわかればトルクなどを考えることができるようになる.そしてそれを表したものが次の図5である.
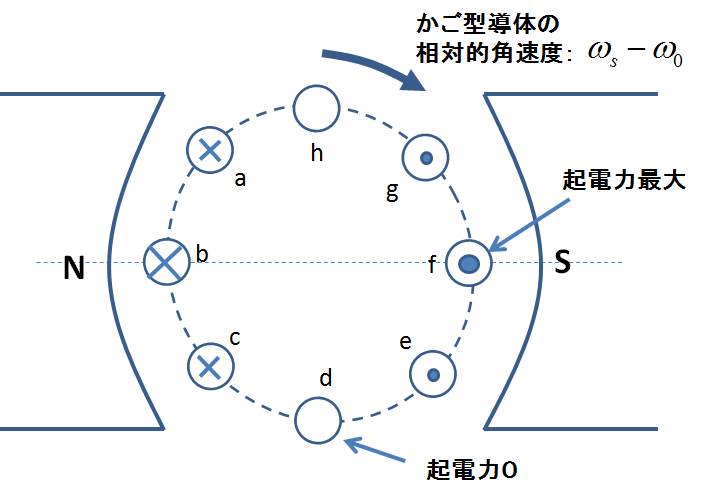
図5.回転磁界から見た誘導電流の強度分布
この図5は,図4で取り出した円筒上に並んだ導体棒アレーの断面図において,個々の導体棒に流れる電流の向きと強さを表したものである.これはかご形導体のインピーダンスが完全に抵抗的であるとしている(インピーダンスが誘導的になる場合は後述).
この電流分布はかごの回転につられて移動することはなく,回転磁界から見て静止しているのである.このことをもう少し詳しく図6で見てみよう.
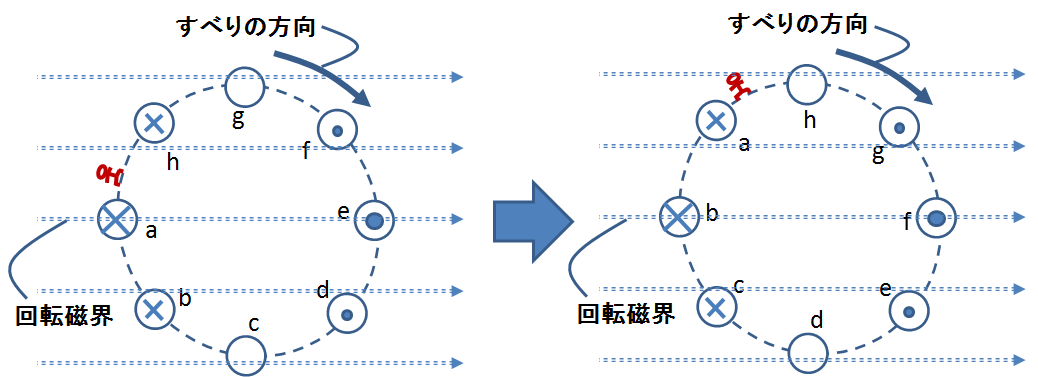
図6.回転磁界から見て誘導電流分布が一定となるイメージ
図6は左側から右側に至るまで\(45^\circ\)回転しているが,電流分布の様子は変わらないことを示している.つまり,例えば導体棒aは\(45^\circ\)回転することにより元々導体棒hがいた場所に移動してくるが,そのとき導体棒aが流す電流量と向きは,かつてそこで導体棒hが流していたそれと同一になるのである.言い換えると,導体に流れる誘導電流の大きさについて導体の区別はなく,純粋にその導体の位置によって決まる電流量が流れるのである.
回転磁界から見て常に一定の誘導電流分布が起きるので,それにより生じるトルクも一定になるはずである.それを示したものが次の図7である.
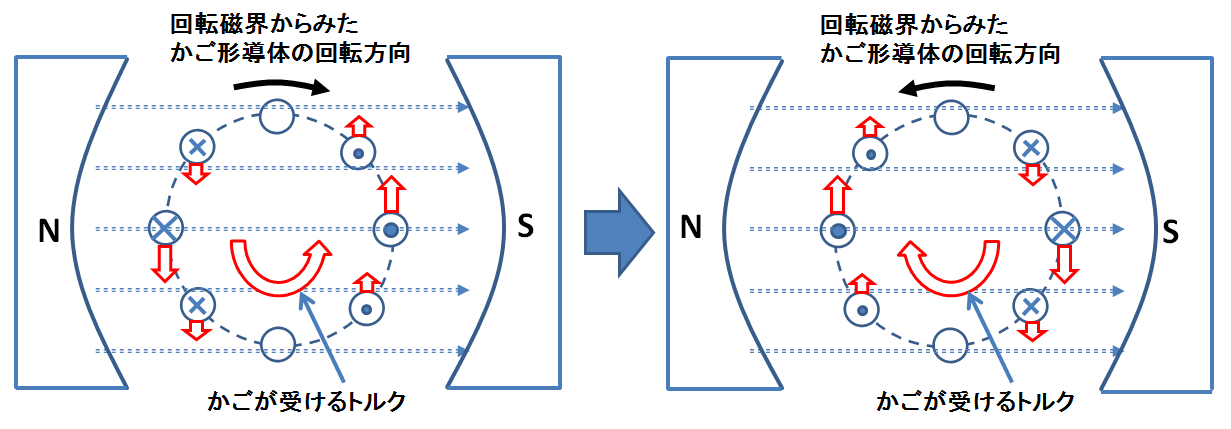
図7.すべりが正の場合(左)とすべりが負の場合(右)のトルクの向き
この図7は,回転磁界の視点に立つと,常にかご形導体の回転方向と逆にトルクが働いていることがわかる.例えばすべりが正の場合,回転磁界が反時計回りに回る角速度よりかご形導体が反時計回りに回転する角速度の方が小さいので,回転磁界から見るとかご形導体は時計回りに回転する.すると誘導電流の分布は図6に示したようになるので,それを基にフレミングの左手の法則でトルクの向きを考えると,反時計回りのかご形導体の回転を助ける向き(反時計回り)にトルクが生じる.
一方ですべりが負の場合,回転磁界から見るとかご形導体は反時計回りに回っているので,生じる誘導電流の向きも正反対になるだろう.ということでそれによって生じるトルクの向きも逆になり,反時計回りの回転を妨げる向き(時計回り)にトルクが生じる.
後述するがこの図7の左側は誘導電動機,右側は誘導発電機として機能する.確かに同図左側は回転方向にアシストするようにトルクが生じているので電力は消費しているはずであり,一方同図右側はかごの回転方向と逆らうようなトルクが発生しているので,電力が交流電源に回生されていて然るべきである.現にそのようになっていることは,誘導機の等価回路などを用いて解析するうち理解できるようになるだろう.
上記の考察を表にまとめると以下のようになる.
$$ 表1.誘導電動機と誘導発電機の違い\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|c|c|c|} \hline \T & \ \ \ 電動機\ \ \ & \ \ \ 発電機\ \ \ \\\hline \ 回転速度\omega_{0}\ & \omega_{0}<\omega_{s} & \omega_{0}>\omega_{s} \\ すべりs & s>0 & s<0 \\ トルク & 回転方向 & 回転と逆方向 \\\hline \end{array} $$
図7ではあたかも発電機と誘導機が逆に回転しているように見えたが,あれはあくまで回転磁界から見たときの話なので,外から見れば電動機動作・発電機動作時ともに反時計回りに回っている(すべりが1以上のケースは別だが).上記の表1は,電動機や発電機を外から観測したときの回転速度やトルクのまとめとなっている.ちなみに\(\omega_{s}\)は同期角速度(すべりが全くないときの回転角速度,言い換えると回転磁界の角速度)である.
これまではかご形導体のインピーダンスが抵抗的であるという想定で話をしてきた.しかしすべり\(s\)が大きくなっていくと誘導電流の周波数も上がるので,かご形導体のリアクタンス成分(漏れインダクタンス)が無視できなくなってくる.このようにすべりが増え,リアクタンス成分が大きくなったときのかご形導体内の電流分布の変化を次の図8に示す.
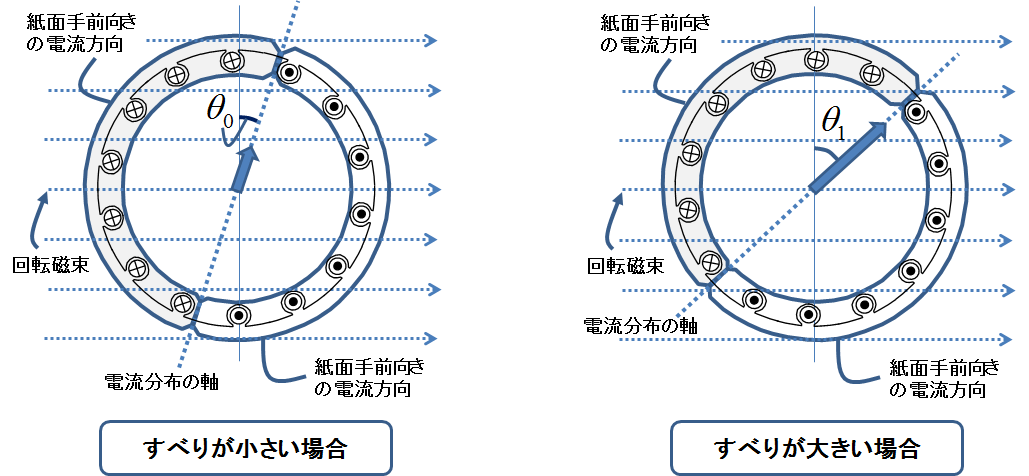
図8.すべりが小さい場合(左)と大きい場合(右)の誘導電流分布
この図8の左側はすべりが小さい場合なので誘導電流の周波数は低く,かご形導体のリアクタンス成分は小さいので電流分布の軸がほとんど直立した形になる.一方で同図の右側はすべりが大きい場合を表しており,誘導電流が高周波になるのでリアクタンス成分が増え,回転磁界に対して電流分布の軸が傾いていく.純粋にリアクタンス成分のみの場合(完全に誘導性の場合)は,この傾き\(\theta_{1}\)は\(90^\circ\)に等しくなる.
また,誘導電流の大きさに関しては,中央の矢印の長さで示している通り,すべりが大きい方がかご形導体に発生する誘導起電力が大きくなるので大電流となる.しかし,トルクもすべりが大きい方が増加するかと言えばそれは別問題である.なぜなら,図8の右側に示したような電流分布の傾きは,トルクに対しては不利に働くからである.この辺りの定量的なイメージは後述する誘導機の解析を追えばすぐに理解できることと思う.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】の§5-2前半にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











