同期機のベクトル図導入

 

　前回の“同期機の電磁気学的解説”での説明を経て，ようやくベクトル図の手法をその物理背景も絡めながら直感的に導入する準備が整った．著書の§４－２で詳しく解説しているベクトル図の手法が持つ物理的意味について，ここではダイジェスト的に紹介していくことにしよう．

　下記の図1は，回転子コイル（ここでも永久磁石でなく巻線形の回転子を想定して話を進める．永久磁石でも同様の議論は成り立つ．）に乗った視点で見たときの，合成磁束（赤矢印）と，それを構成する回転子コイルによる磁束（青矢印）と電機子電流による磁束（黒矢印）を矢印で示したものである．

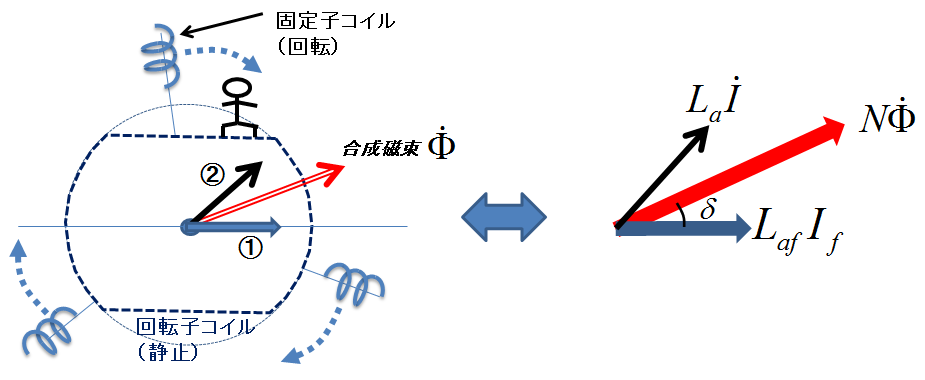
図1.回転子上の観測者から見た同期機の磁束と電流

 

　前回の記事からもわかるが，回転子上で観測すると，これらの磁束はすべて静止して見える．なぜなら磁束は回転子と全く同じ回転速度で同じ向きに回転しているからである．そこで，回転子上の視点において，これら一定のベクトル量の可算や減算をすることで同期機の電磁気学を扱う手法を確立できれば，同期機の解析が圧倒的に楽になりそうだという直感が湧いてくるだろう．これこそが，ベクトル図の思想そのものなのである．

　それでは，これからこの図1を出発点にして，同期機の起電力や流れる電流などを付きとめていくことにしよう．

まず，固定子コイルを貫く合成磁束を\(\dot{\Phi}\)とすると，電機子電流\(\dot{I}\)による磁束\(L_s\dot{I}\)（電機子反作用）と回転子コイルの励磁電流\(I_f\)による磁束\(L_{af}I_f\)を用いて，

$$N\dot{\Phi}=L_s\dot{I}+L_{af}I_f \tag{1}$$

　と表すことができる．（磁束や電流方向の定義によっては符号逆．ベクトル図への影響は後述）

　この式からわかることは，合成磁束というのは基本的にこの2つの磁束（電機子反作用の磁束と励磁電流による磁束）の合成だということである．ここで，\(N\)は固定子巻線の巻き数である．また，\(\dot{\Phi}\)や\(\dot{I}\)をフェザー表示（複素数表示，文字の上のドットが目印）にしているのは，複素数を使うと2次元ベクトル量が代数的かつシンプルに表現できるからである．ここでは回転子コイルの磁束を実軸においているので，\(L_{af}I_f\)は実数としている．

　これで，電流と磁束の関係は分かった．次は同期機の端子電圧が，上記からどのように導かれるのか説明しよう．同期機の端子電圧は，ファラデーの法則から導かれる．つまり，電機子コイルを通り抜ける磁束の変化が同期機の端子電圧と等しくなるのである．次の図2を用いて説明しよう．

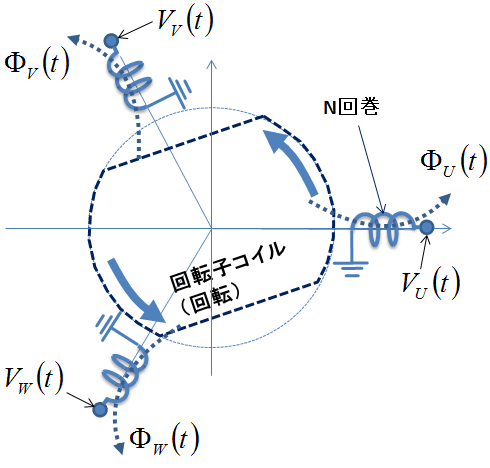
図2.同期機の電機子コイルを貫く磁束と起電力

 

　このように各相のコイルの電圧と磁束を定義すると，両者の間には下記のファラデーの法則が成り立つ．

$$V_k(t)=N\frac{d\Phi_k(t)}{dt}\; \; (k=U,V,W) \tag{2}$$

　定義によっては右辺の符号が逆になるが，一般的な同期機の教科書の定義にならい，今回は同期機に電流が流入した場合に磁束の符号が＋になるように磁束の極性を定義したので，式（2）の右辺にはマイナスの符号がない．（物理法則そのものの符号だけ誤らなければ，計算過程における極性の定義の違いで物理現象の予測結果が変わることはあり得ないので，余り神経質にならないでもいい．）

　この時間微分をフェザー表示に直すと，以下のようになる．

$$\dot{V}=j\omega N\dot{\Phi} \tag{3}$$

　時間微分はフェザー表示の上では\(j\omega\)を掛けることに相当するのである．これで，同期機の端子電圧についても求めることができた．式（1）と式（3）によって，同期機の磁束・電流・電圧の3者の関係を導くことができたのである．式（1）に\(j\omega\)を掛ければ，

$$j\omega N\dot{\Phi}=j\omega L_s\dot{I}+j\omega L_{af}I_f \tag{4}$$

　これに式（3）を代入すれば，

$$\dot{V}=j\omega L_s\dot{I}+j\omega L_{af}I_f \tag{5}$$

　ここで，

$$X_s\equiv \omega L_s$$ $$\dot{E}=j\omega L_{af}I_f$$

　とおけば，

$$\dot{V}=jX_s\dot{I}+\dot{E} \tag{6}$$

となる．これが同期機のベクトル図においてもっとも重要な式である．つまり，式（1）に\(j\omega\)を掛けることで式（6）に変換されたので，これをベクトル図上で表現すると，下記の図3のようなイメージになる．

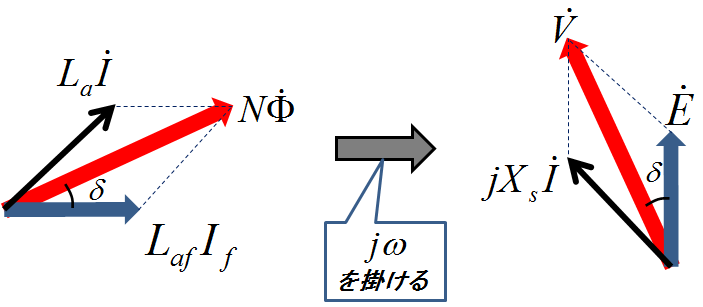
図3.同期機の磁束から電圧・電流のベクトル図へ

 

　左側は式（1）を，右側のベクトル図は式（3）を表している．右側は端子電圧\(\dot{V}\)と起電力\(\dot{E}\)，電機子電流\(\dot{I}\)による電圧\(jX_s\dot{I}\)の間の関係を示しており，同期機のベクトル図そのものである．

 

　ここまで，電流・電圧・磁束がすべて回転子と同じ回転速度で回転するベクトル（複素数）として扱ってきたが，これが実際の同期機と対比して，どのような電気的意味を持つのか，ここで一度整理しておくことにしよう．

　次の図4では電機子電流が回転子と同じ速度で回転する複素数で表現できることを示している．

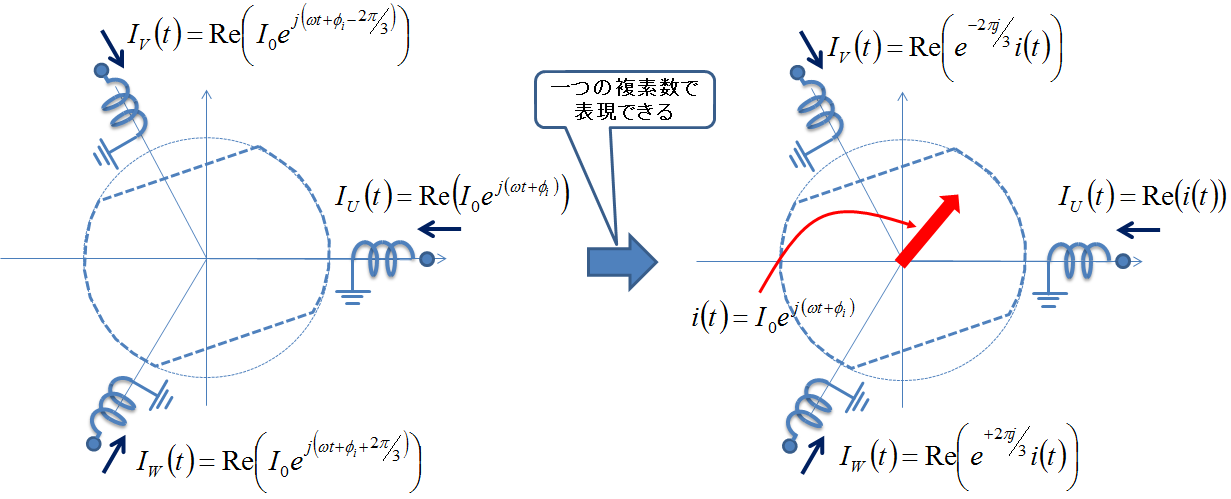
図4.同期機の電機子電流が複素数で表されるイメージ

 

　理想的な三相交流であれば（正相成分のみならば），どれか1相の振幅と位相が決まれば他の2相の振幅と位相も確定する．理想的な三相交流は，3相とも振幅は等しく，位相は\(120^\circ\)ずつ異なるからである．ということは，図4に示すように，3つの電機子電流は回転子コイルと同じ角速度\(\omega\)で回転する次のような複素数1つで代表できる．

$$i(t)=\dot{I}e^{j\omega t} \tag{7}$$

　ちなみに，これを各相の電流に焼き直すには，下記のような計算をすればよい．

$$I_U(t)=Re(i(t)) \tag{8-1}$$ $$I_V(t)=Re(e^{\frac{-2\pi j}{3}}i(t)) \tag{8-2}$$ $$I_W(t)=Re(e^{\frac{2\pi j}{3}}i(t)) \tag{8-3}$$

　また，これと同様に電圧や磁束についても下記のような複素数で代表させることができる．

$$v(t)=\dot{V}e^{j\omega t},\phi(t)=\dot{\Phi}e^{j\omega t} \tag{9}$$

　この定義を見ると，ベクトル図における\(\dot{V}\)や\(\dot{I}\)などの大きさは，1相分のフェザー表示と等価であることがわかるだろう．1相分の実効値なのか波高値なのかは，文献により異なる

　ここで，鎖交磁束数\(\dot{\Psi}\)という物理量もよく登場するので下記に定義を示す．

$$\psi(t)=N\phi(t),\dot{\Psi}=N\dot{\Phi} \tag{10}$$

　\(N\)は電機子コイルの巻数である．これを用いれば，式（1）や式（3）は下記のようによりシンプルに表される．

$$\dot{\Psi}=L_s\dot{I}+L_{af}I_f \tag{1'}$$ $$\dot{V}=j\omega\dot{\Psi} \tag{3'}$$

　回転機をはじめとする，コイルを伴う磁気回路の解析においては，磁束よりもむしろ鎖交磁束数を用いて定式化することの方が圧倒的に多いので，この表現にも慣れておかれるとよいだろう．

　次からは，このベクトル図の導入を踏まえて，ベクトル図の基本的な性質の紹介や，同期機の等価回路の導出，またベクトル図のPU化などを紹介していく．

 

 

 

 

この項の内容に関する，より詳細で完全な解説は，

【徹底解説　電動機・発電機の理論】の§４－２前半（P.144～）にて展開されています．是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス