誘導機の円線図法について
この記事では,誘導機の円線図について,その詳しい数理的な扱い方というよりは,円線図自身が持つざっくりとした意味とそのイメージを解説していく.まず,円線図の根源ともなるイメージを図1に紹介しよう.
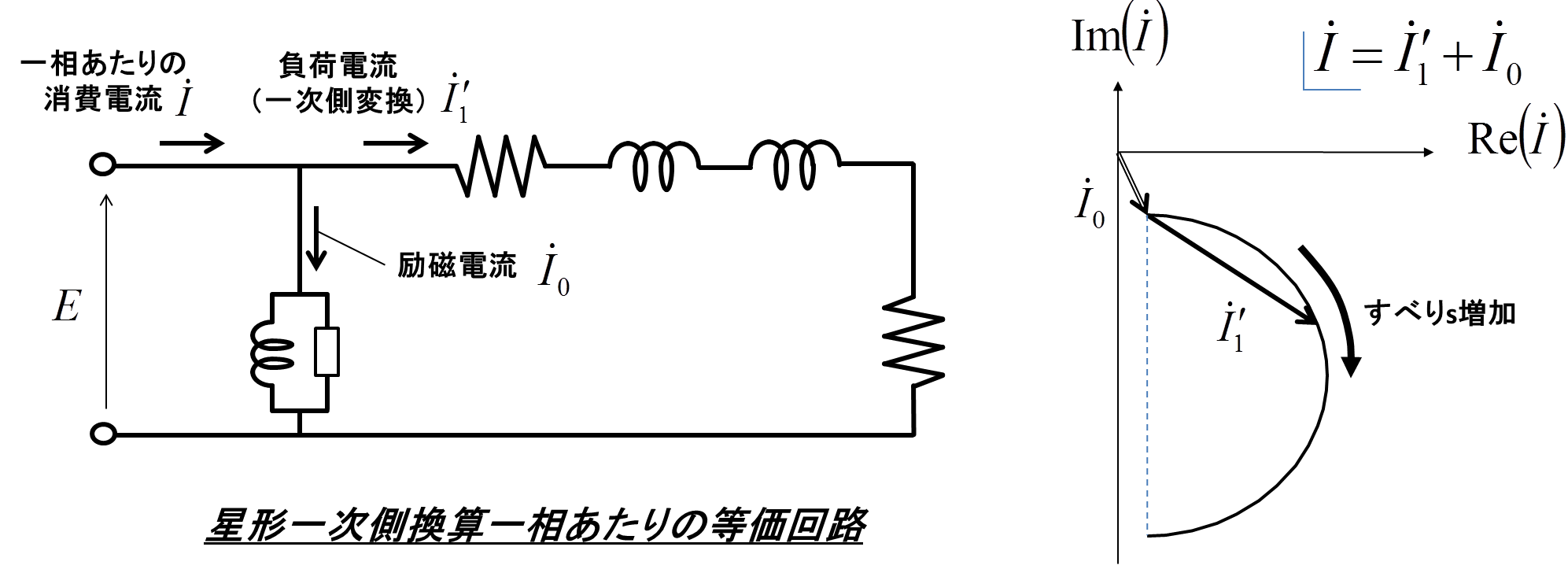
図1.等価回路と円線図の対応関係
この図1は,いままで解説してきた誘導機の等価回路と円線図との対応関係を示している.円線図の半円を一言で表すならば,「電機子電流\(\dot{I}\)のフェザー表示における軌跡」となる.実際に図1が示すように,L型等価回路の励磁電流\(\dot{I}_{0}\)はすべり\(s\)によらず一定で,負荷電流\(\dot{I}_{1}^{'}\)はすべり\(s\)に応じて半円の軌跡を描く(図1のケースの場合\(s>0\)).
そして,このように電機子電流のフェザー表示にした時点で,以下の図2に示すように力率角や消費電力などの情報を目の子で読み取ることができるだろう.

図2.円線図と力率角・消費電力
この図2の真ん中の図は,電機子電流の位相がそのまま力率角となることを示しており当然のことを言っている.また,右側の図は電機子電流の実軸成分に比例した電力消費があることを示しておりこれも相電圧\(E\)が実軸上としているので当然の結果である.実際の円線図はこの図2からは反時計回りに\(90^{\circ}\)回転させたものなのでその違いはあるものの,基本的には目の子で力率角や消費電力の多寡を読み取ることができる.
次の図3は,消費電力を図形的に機械的出力+一次銅損+二次銅損へと仕分けするためのイメージを示している.
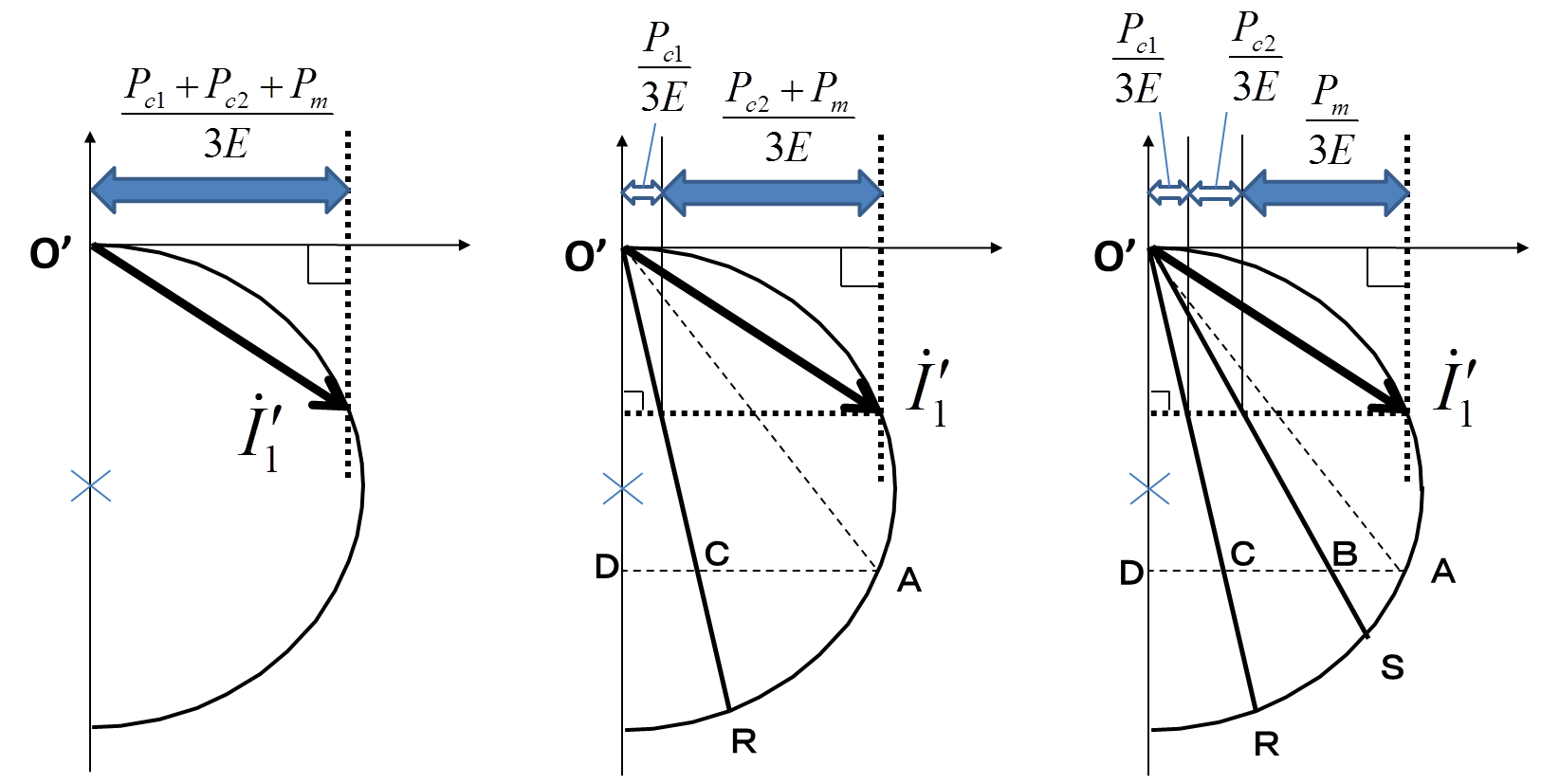
図3.消費電力の仕分け方
この図3は簡単のために励磁電流\(\dot{I}_{0}\)を無視して,負荷電流部分\(\dot{I}_{1}^{'}\)だけの消費電力に着目している.\(\dot{I}_{1}^{'}\)の実部は機械的出力+一次銅損+二次銅損の3つの要素の足し合わせとなっているので,この3つを作図的に分離したい.そこで登場するのか,この図3の左側に存在する線分\(O^{'}S\)と線分\(O^{'}R\)である.この2本の線分で,消費電力を3つの成分に分割することができるようになる.
具体的に説明しよう.この図3の左側の点\(A\)に注目する. 電機子電流が点\(A\)に達したときの消費電力は線分\(AD\)の長さに比例する.そして先ほどの2つの線分\(O^{'}S\)と\(O^{'}R\)により線分\(AD\)は3分割されていることがわかる.
この\(AB:BC:CD\)こそが,機械的出力:二次銅損:一次銅損の比に等しくなっているのである.
では,なぜこのように直線で分割できるのか?それに答えるためには,\(O^{'}A\)の長さの2乗は線分\(CD\)や線分\(BC\)に比例しているという幾何学的な性質が説明できればよい.そうすれば線分負荷電流\(\dot{I}_{1}^{'}\)の大きさは線分\(O^{'}A\)の長さに比例し,その2乗が銅損に比例するので,銅損は線分\(CD\)などに比例すると言えるのだ.この幾何学的な性質は高校2年の数学を用いて証明できる.
ということで,機械的出力や一次銅損,二次銅損が円線図上で下記の図4のように表されることがわかる.
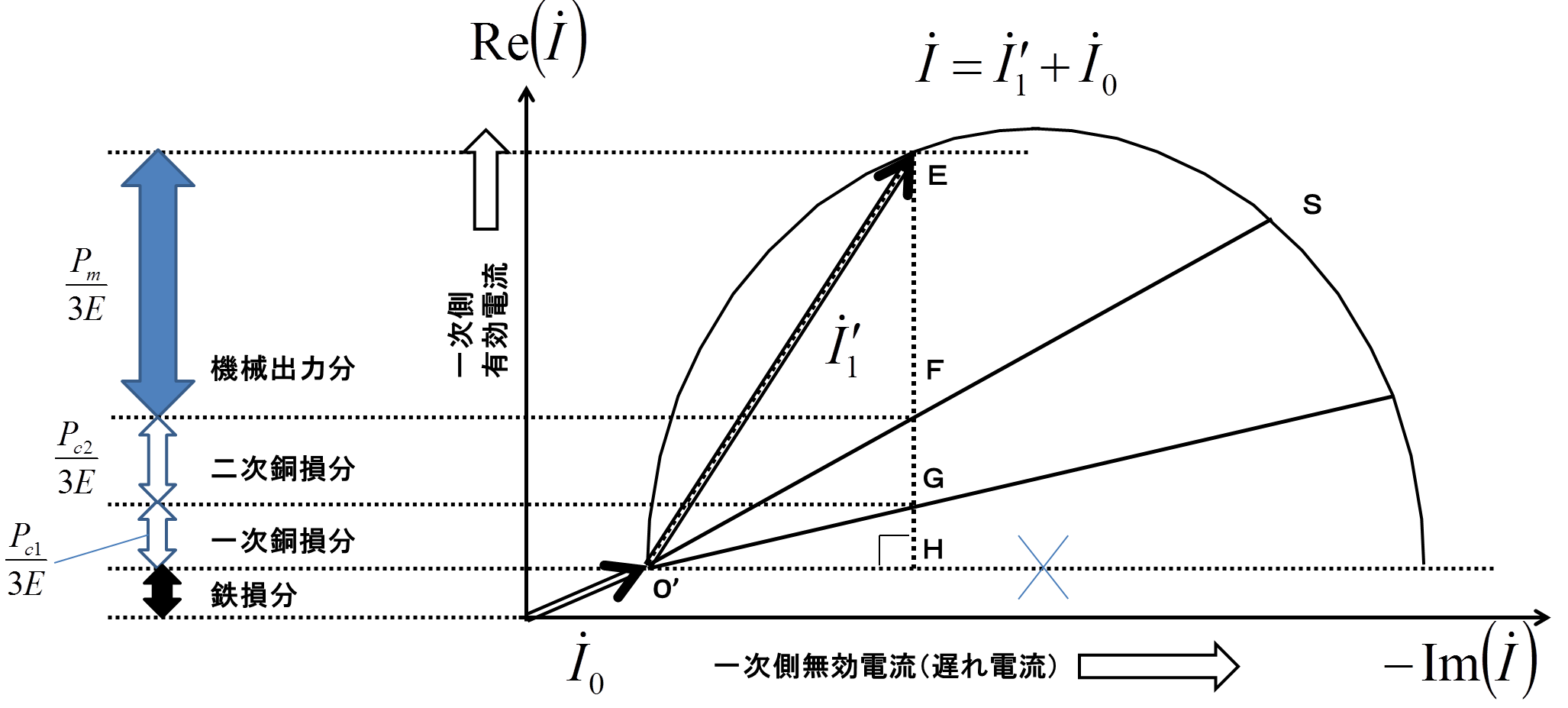
図4.誘導機の円線図法
この図4では,励磁電流\(\dot{I}_{0}\)が加わっているので,その縦軸成分が鉄損となって加わっている.機械的出力・二次銅損・一次銅損の区分は図3で示した通りである.そして円線図は,通常のフェザー表示を反時計回りに\(90^{\circ}\)したものだともわかる.つまり,円線図の矢印(電流ベクトル)の横軸成分は遅れ無効電流を,縦軸成分は有効電流成分をそれぞれ表すことになる.すなわち矢印が倒れることは力率の悪化を示している.そして点\(E\)が点\(S\)に達したとき,すべりが\(s=1\)になることを確認してほしい(回転が止まり,機械的出力が0になるため).
最後に簡単に円線図の作図方法について触れておこう.下の図5を見て欲しい.
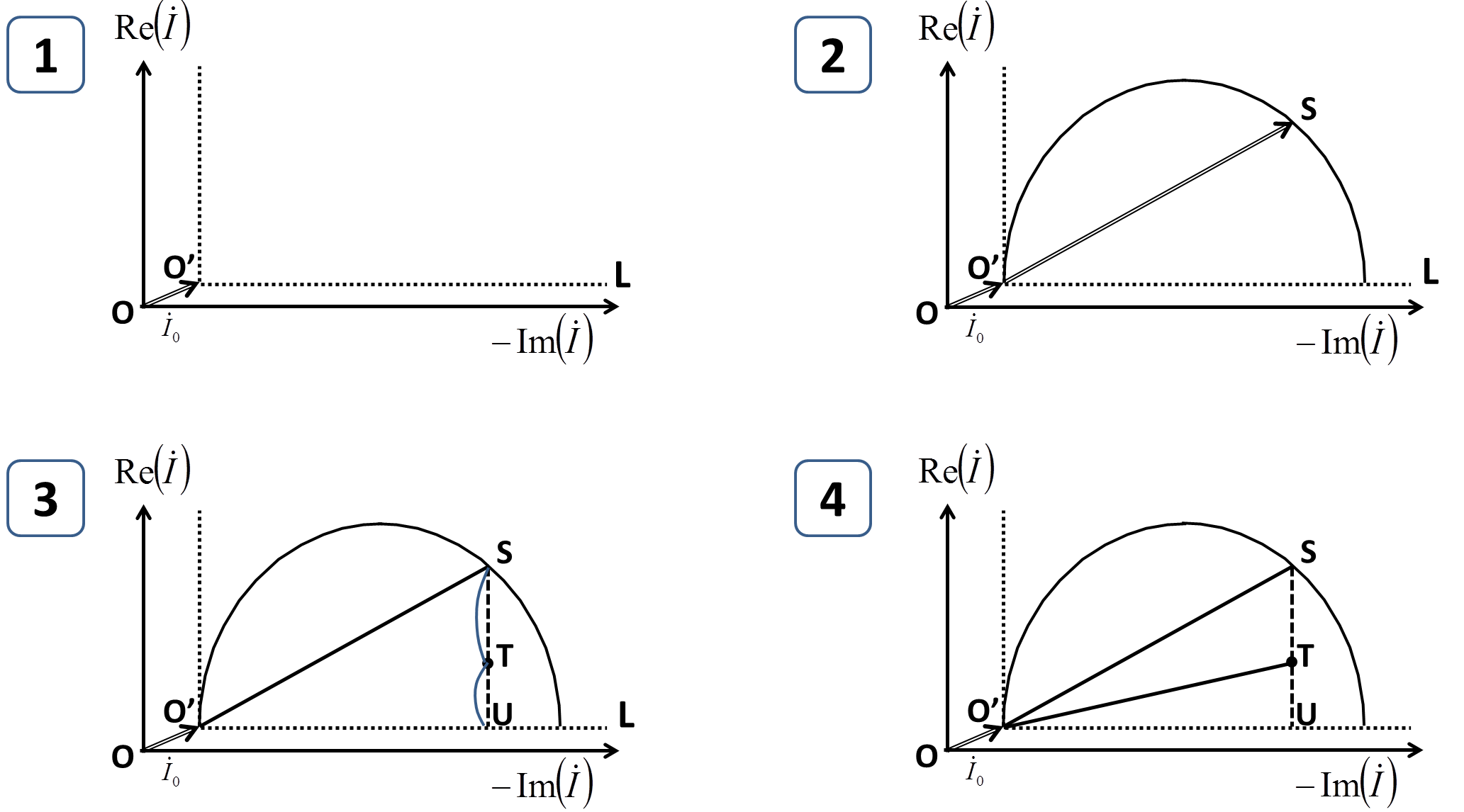
図5.円線図法の作図方法
図5の4つのステップを説明すると以下のようになる:
1.励磁電流\(\dot{I}_{0}\)を無負荷試験で測定して点\(O^{'}\)を記入する.
2.すべり\(s=1\)のときの負荷電流を拘束試験により割り出し,点\(S\)を記入する.
3.水平な直線\(O^{'}L\)に点\(S\)から垂線を下し,垂線の足を\(U\)とする.
4.線分\(SU\)を,\(ST:TU=r_{2}^{'}:r_{1}\)になるように点\(T\)を定める.\(r_{1}\)は端子間抵抗測定で,
\(r_{2}^{'}\)はそれに加えて拘束試験の消費電力から計算する.そして線分\(O^{'}T\)を引いて完成.
これで円線図の物理的イメージは大分湧いたのではないだろうか.円線図を用いた見積もりはJISの標準ではなくなったものの,粗くでも特性を視覚化したいときなどに威力を発揮する.また,前回の記事に示した複雑な計算式の意味が意外とシンプルであるという感触を得るためにも,教育的に有効なツールであり続けると筆者は考えている.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】の§5-3終盤にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











