誘導電動機の機械的出力・トルク・力率・各種損失

　ここまでの記事では，誘導機の等価回路の物理的な意味を説明してきた．ここからは，ついに等価回路を用いた特性計算を行っていく．機械的出力，トルク，力率，効率などが等価回路を用いて計算できることがわかるだろう．まず最初に，誘導機の等価回路にはT型とL型の２つのタイプがあることを説明しよう．

図1.誘導機のT型等価回路（左）とL型等価回路（右）

　この図1の左側がT型，右側がL型である．両者の違いは，励磁電流モデルを表すインダクタと抵抗の並列回路の位置である．T型は励磁電流部分が真ん中なので確かにT字形になり，L型は励磁電流部分が電源側に引っ越しているので，L字形を時計回りに倒したような形になっているだろう．より現実に近いのはT型だが，トルクなどの計算がしやすいのは圧倒的にL型なので，ここではL型等価回路を用いて説明をしていこう．（多くの教科書でもL型で説明している．低周波・低電圧動作時でないかぎり，L型とT型の計算結果はほぼ一致）

　まず最初に明らかにしたいことは，図1の等価回路のどの抵抗が機械的出力の電力消費を表現しているのかを知るところからであろう．図2を見ていただきたい．

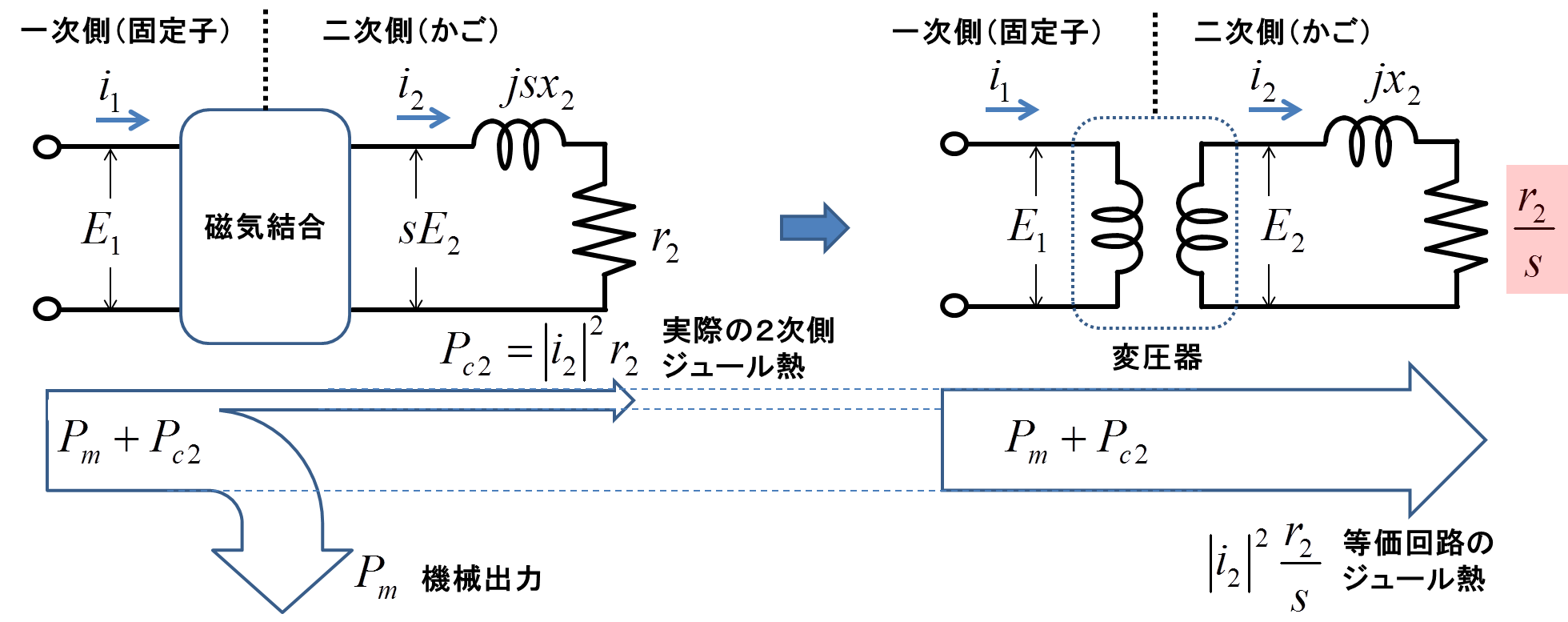
図2.機械的出力$P_{m}$と二次銅損$P_{c2}$の内訳

　この図2では，実際の誘導機の消費電力内訳（左）と等価回路による二次側抵抗$\frac{r_{2}}{s}$での消費電力（右）との比較を行っている．電源側（図の回路の左側）から見れば，両者は完全に一致するはずである．つまり二次側抵抗$\frac{r_{2}}{s}$での消費電力は1相分の機械的出力$P_{m}$と1相分の二次銅損$P_{c2}$の和，すなわち$P_{m}+P_{c2}$となっているはずである．実際の1相分の二次銅損$P_{c2}$は，抵抗値$r_{2}$に電流$i_{2}$が流れているので

$$ P_{c2} = \left| i_{2} \right|^{2}r_{2} \tag{1} $$

となる．一方で等価回路による二次側抵抗$\frac{r_{2}}{s}$での消費電力が$P_{m}+P_{c2}$と等しいことにより

$$ P_{m}+P_{c2} = \left| i_{2} \right|^{2}\frac{r_{2}}{s} \tag{2} $$

式（1）と式（2）の差分を取って，

$$ P_{m} = \left| i_{2} \right|^{2}r_{2}\frac{1-s}{s} \tag{3} $$

これにより，等価回路（1相分）のうちの機械的出力$P_{m}$を計算することができた．

　なぜ，実際の二次銅損と等価回路による二次側抵抗の消費電流の差がまるまる機械的出力になるのか，その物理的なイメージは関連著書をチェックいただくとしてここでは割愛する．

　さて，上記の式（1）～（3）から，等価回路の二次側抵抗$\frac{r_{2}}{s}$をどのように２分割すれば，丁度$P_{m}$と$P_{c2}$が消費電力となるような抵抗値に分割できるのか，簡単にわかる．

$$ \frac{r_{2}}{s} \rightarrow r_{2} + r_{2}\frac{1-s}{s} \tag{4} $$

これを踏まえると，トルクなどの計算には，以下の図3のような二次側等価抵抗を分割した等価回路が便利である．

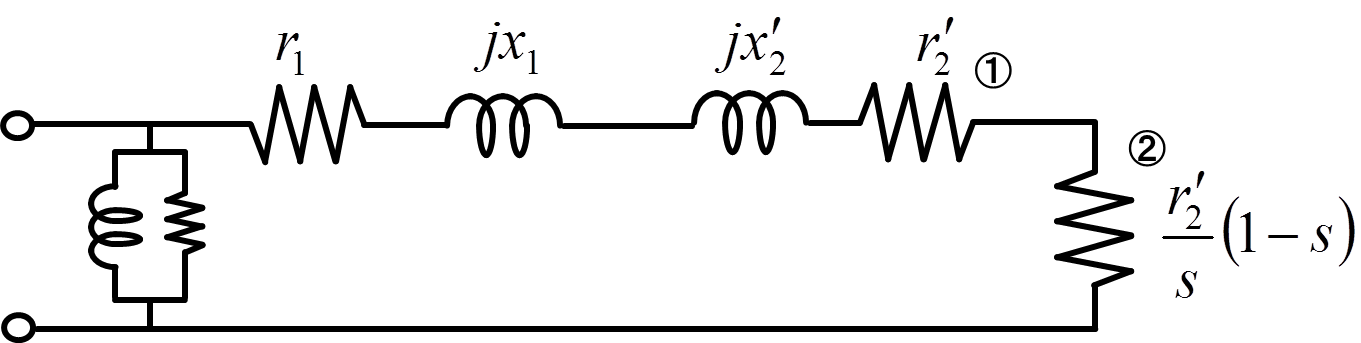
図3.抵抗を２分割（①は二次銅損向け，②は機械的出力向け）

　この図3の①で消費される電力は１相分の二次銅損，②で消費される電力は１相分の機械的出力となる．それでは，このL型等価回路を用いてこれから機械的出力・トルク・力率・効率などを求めていくべく，下記の図4のように等価回路のパラメータを定めよう．

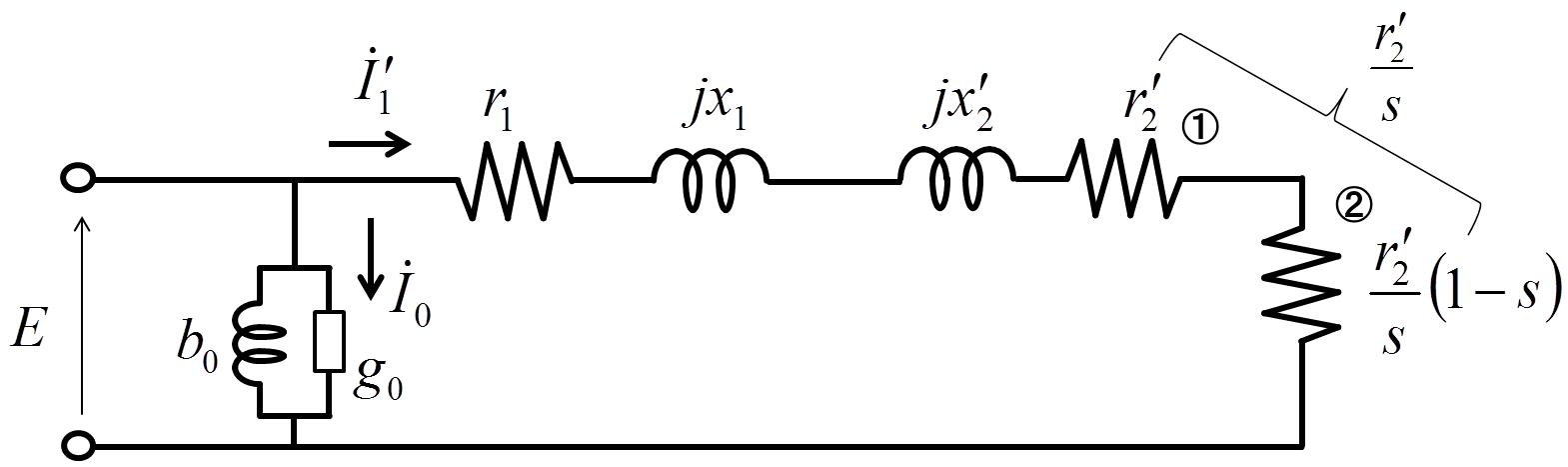
図4.誘導電動機の機械的出力を求めるための等価回路

　励磁電流部分についてはサセプタンスを$b_{0}$，コンダクタンスを$g_{0}$とおいた．また，星形一次換算の1相分の等価回路として，一次側抵抗$r_{1}$，一次側リアクタンス$x_{1}$，二次側抵抗$r_{2}$，二次側リアクタンス$\frac{r_{2}^{'}}{s}$としている．

　この等価回路について，機械的出力$P_{m}$，一次銅損$P_{c1}$，二次銅損$P_{c2}$，鉄損$P_{i}$がどの抵抗の消費電力に対応しているのか示したものが下記の図5である．

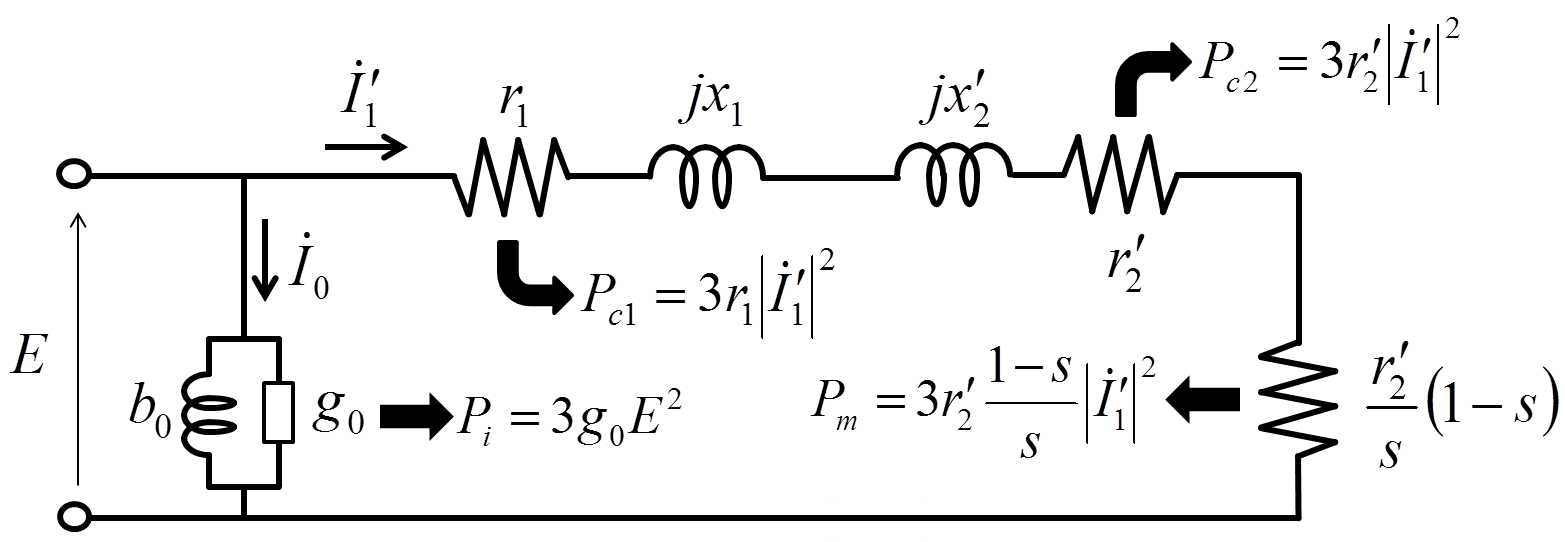
図5.機械的出力$P_{m}$，一次銅損$P_{c1}$，二次銅損$P_{c2}$，鉄損$P_{i}$

　軒並み$3$のファクターが付いているのは，機械的出力$P_{m}$，一次銅損$P_{c1}$，二次銅損$P_{c2}$，鉄損$P_{i}$を$1$相分ではなく電動機全体（$3$相分）として考えているからである．ちゃんと整理して書くと以下のようになる．

機械的出力

$$ P_{m} = 3r_{2}^{'}\frac{1-s}{s}\left| \dot{I}_{1}^{'} \right|^{2} \tag{5} $$

一次銅損

$$ P_{c1} = 3r_{1}\left| \dot{I}_{1}^{'} \right|^{2} \tag{6} $$

二次銅損

$$ P_{c2} = 3r_{2}^{'}\left| \dot{I}_{1}^{'} \right|^{2} \tag{7} $$

鉄損

$$ P_{i} = 3g_{0}E^{2} \tag{8} $$

ここで一次換算負荷電流$\dot{I}_{1}^{'}$が求まれば，上記は全部計算できる．$\dot{I}_{1}^{'}$は，インピーダンスが$\left( r_{1}+\frac{r_{2}^{'}}{s}\right)+\left( jx_{1}+jx_{2}^{'}\right)$の経路に相電圧$E$がかかっているときに流れる電流なので，

$$ \dot{I}_{1}^{'} = \frac{E}{\left( r_{1}+\frac{r_{2}^{'}}{s}\right)+\left( jx_{1}+jx_{2}^{'}\right)} \tag{9} $$

と求められる．また，励磁電流$\dot{I}_{0}$も求めておけば，