光源の物理１（熱放射）

 

　白熱電球は，電球内のフィラメントを非常に高温にすることにより光を発生させている．ここで素朴な疑問が生じる．なぜ高温にすると光が発生するのか？経験的には当たり前だが，ここでしっかりと物理的にも考察しておきたい．

　まず，あらゆる物質からは，その物体の熱に応じた電磁波（光）を放出しているという事実をおさらいするところから始めよう．この事実を理解するため，次の図1に示すような簡単な実験を考えてみよう．

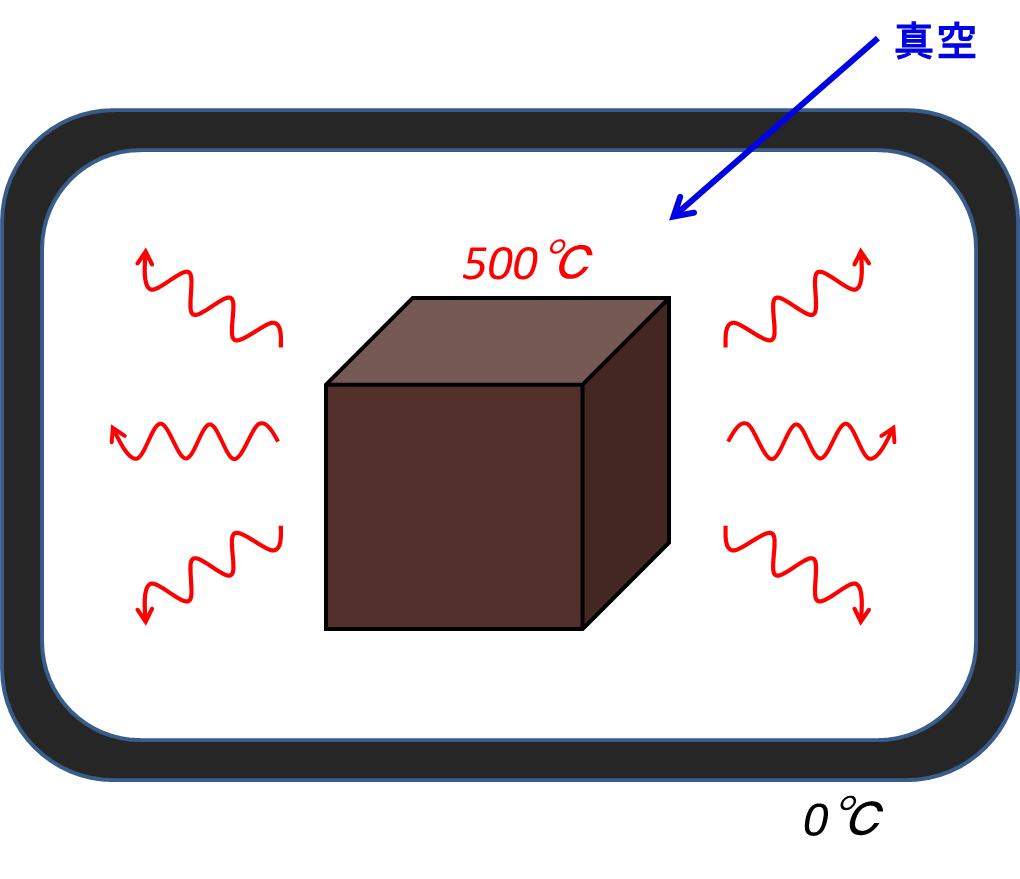
図1.熱放射（放射による冷却）

 

　図1に示した状況は，高温（この例では500℃）の物体が真空中に置かれており，その周りを0℃の冷たい壁で囲んでいるというもので，真空であるにも関わらず500℃の物体からは熱が逃げ，冷えていく．それはこの物体から電磁波の放射が起きているためである．有名な自然現象で言えば，夜間において地表から電磁波（赤外線）が放射されて熱が宇宙空間に逃げるという現象（放射冷却）が挙げられるだろう．

　まったく同じような議論だが，念のため図2において今度は壁の温度の方を高温にしたときの状況も考察してみよう．

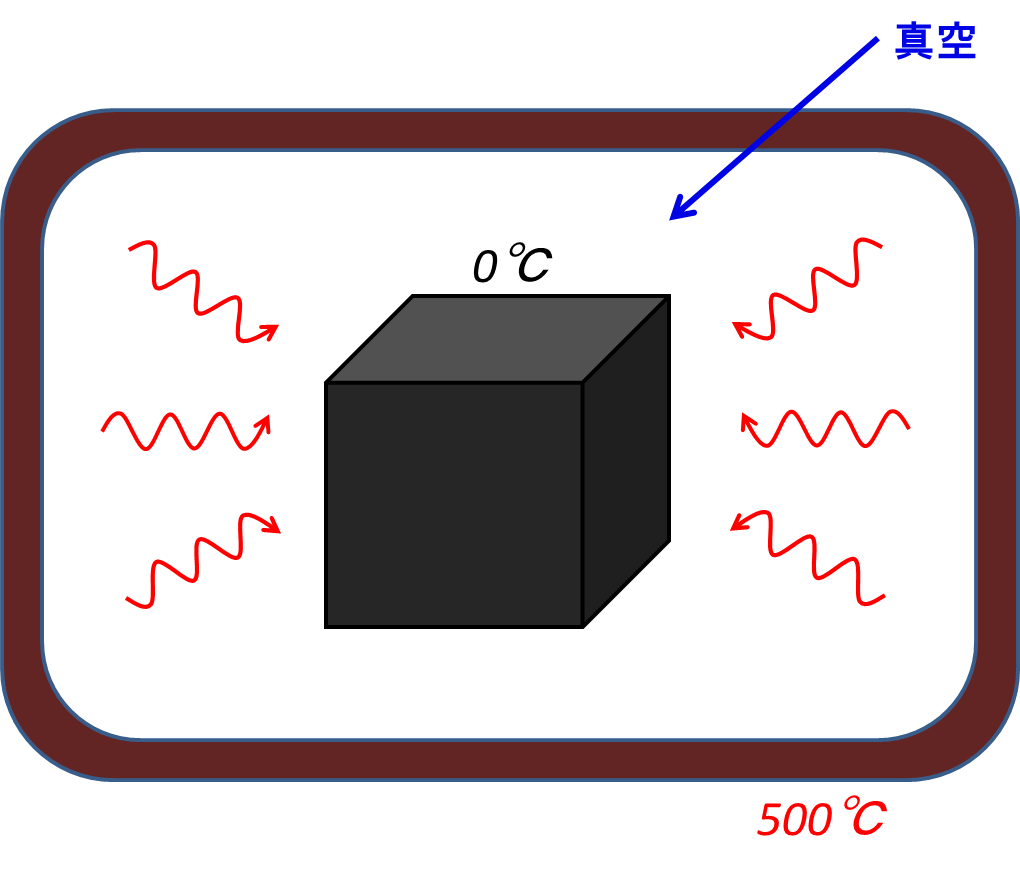
図2.熱放射（放射による加熱）

 

　壁が高温（500℃）で，真空を介して中央に0℃の冷たい物体があるとする．すると今度は壁から発せられる電磁放射の方が強いので，真ん中の物体に熱が流れ込むようになり，温度は壁の温度に漸近していく．壁から物体に赤外線が放射され，物体が昇温していくという，言わばオーブンとしての役割を果たすのである．

　では，このオーブンの中に飛び交う電磁波（光）のスペクトル強度分布はどのようになっているだろうか？それは温度によってどのように変化するのであろうか？図3をご覧いただきたい．

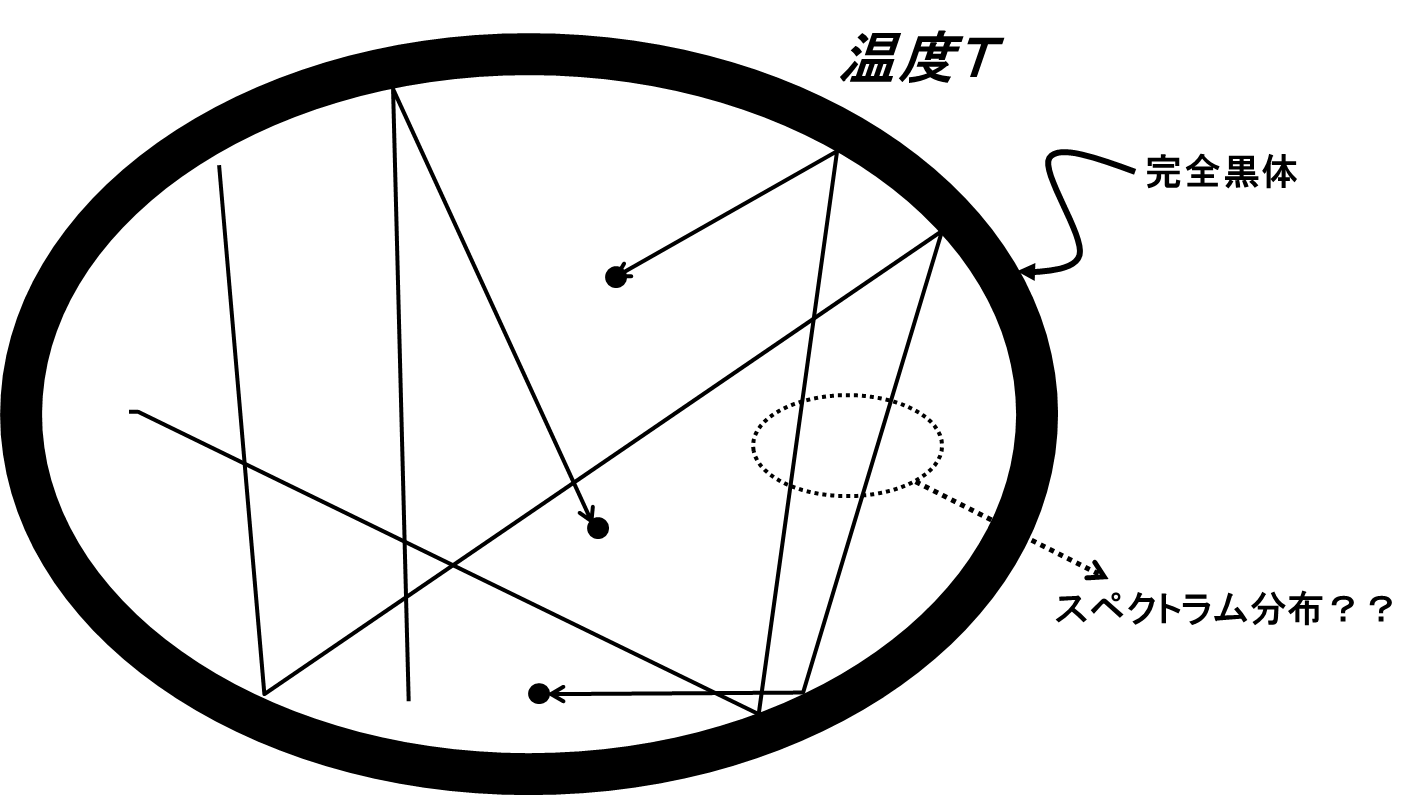
図3.黒体輻射              

 

　完全黒体で囲まれた真空に，どのような赤外線や可視光線，紫外線などの電磁波が飛び交っているのか．結論から言えば，次の図4に示すようなスペクトル分布になる．温度は\(T_{1}>T_{2}>T_{3}\)としている．

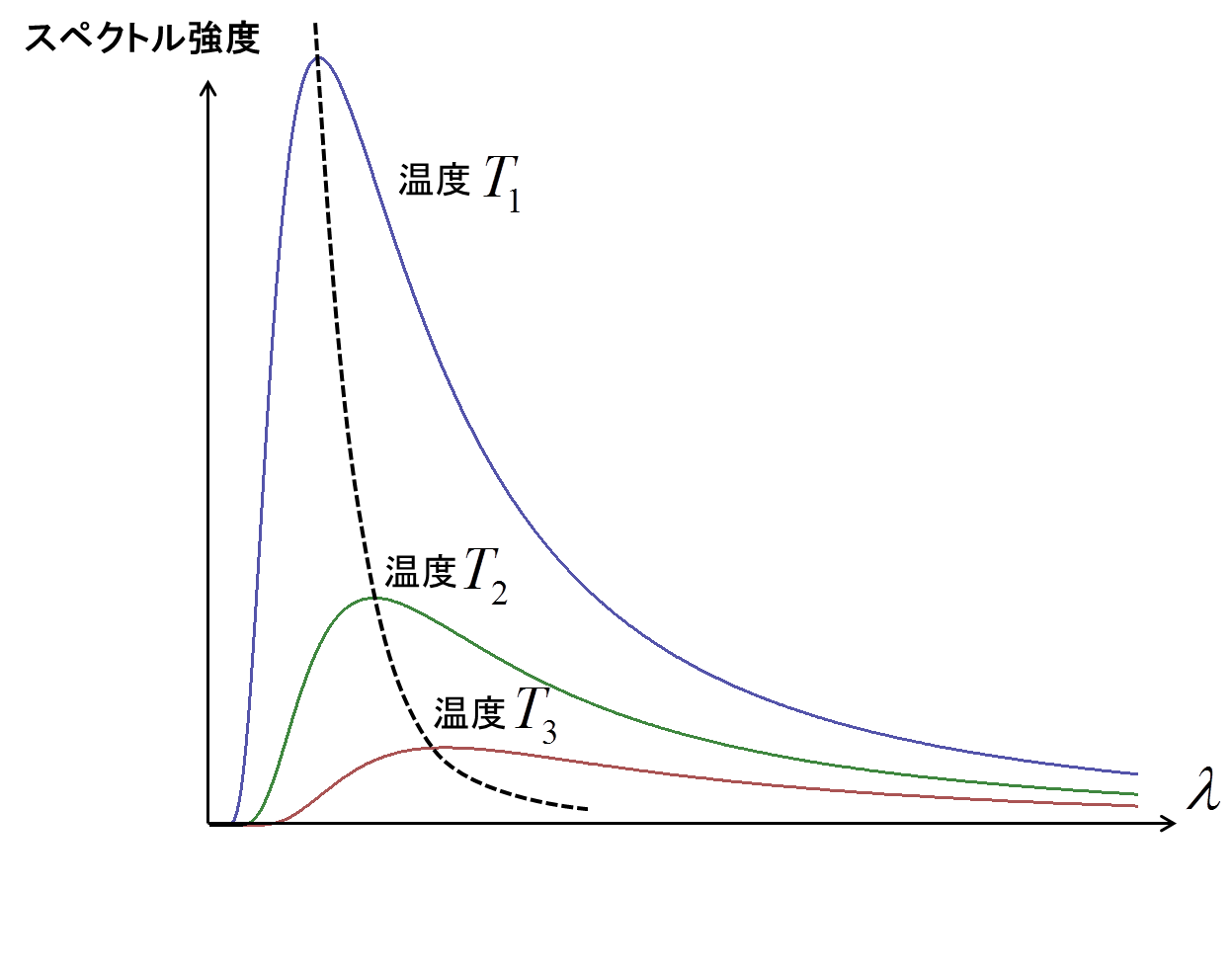
図4.黒体輻射のスペクトル分布

 

　温度が大きい方がすべての波長において放射強度が大きくなっており，ピークとなる波長も短波長になることが伺える．これはどのような物理法則が関連していて，具体的にどのような関数になっているのだろうか？

　まず，この関数の背後にある物理法則として量子力学と統計力学を学ぶ必要がある．ここではその概要を，できるだけ簡潔に紹介していく．

　温度という熱力学的量と，電磁波という電磁気的な量はどうやって結ばれるのか？古典的に言うと，温度\(T\)というのは，ある物理的モード（自由度）1つに対して均等に\(k_{B}T\)というエネルギーが分配される状態と言える．ここで我々が今から考えていく電磁波のモード（自由度）と言えば，電磁波の定在波の数を数えればよい．つまり，以下の図5のように左境界と右境界で同じ状態になる状況（周期的境界条件）における電磁波群を考え，その一つ一つの単一周波数の定在波を１つの固有状態（物理的な自由度）として解析をしていけばよい．

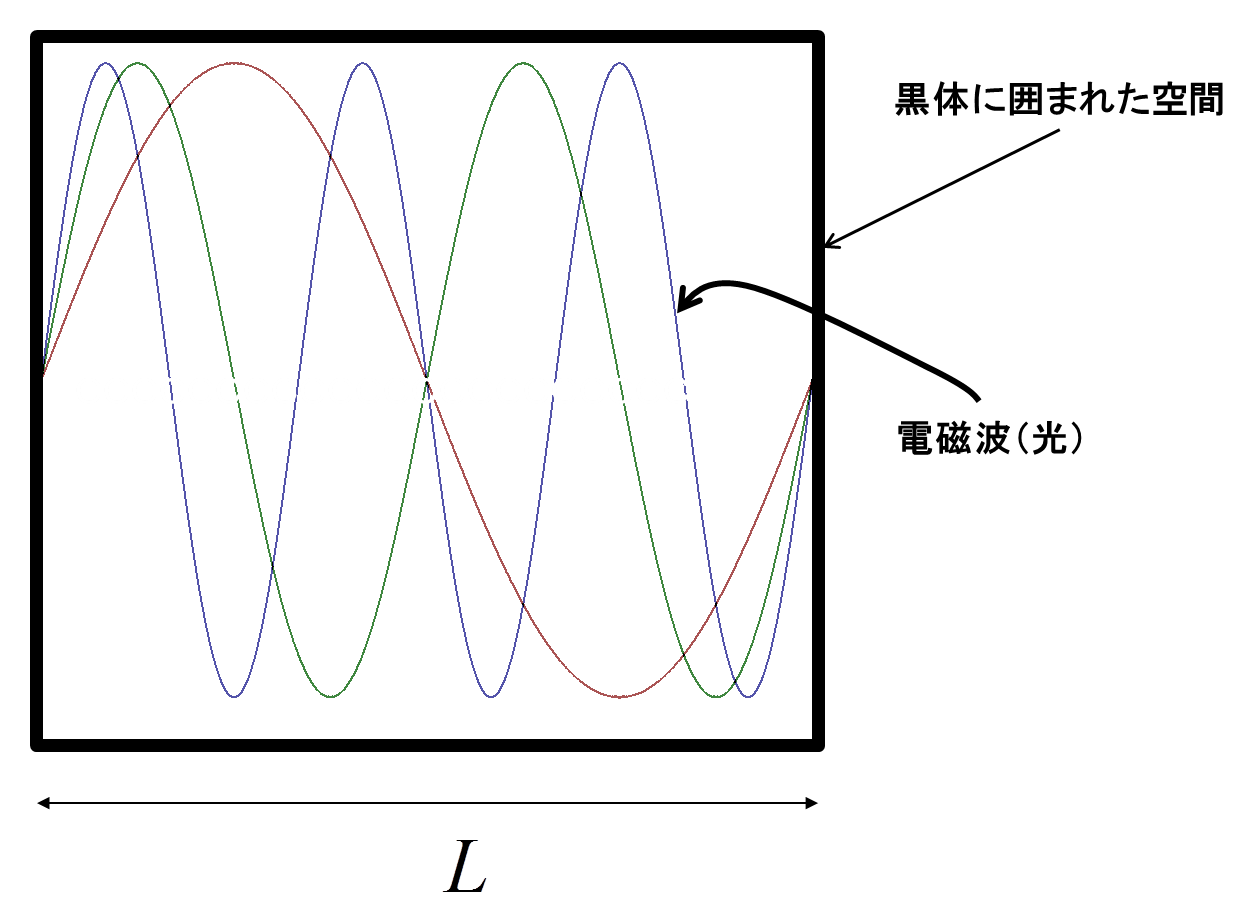
図5.電磁波（光）の定在波            

 

　この図5は一次元の周期的境界条件における定在波一つ一つを表しているが，実際扱うオーブンの中は３次元空間なので，これでは不足である．しかしいきなり３次元での定在波の説明は難しいので，次の図6で2次元の周期的境界条件における電磁波の定在波イメージから説明しよう．

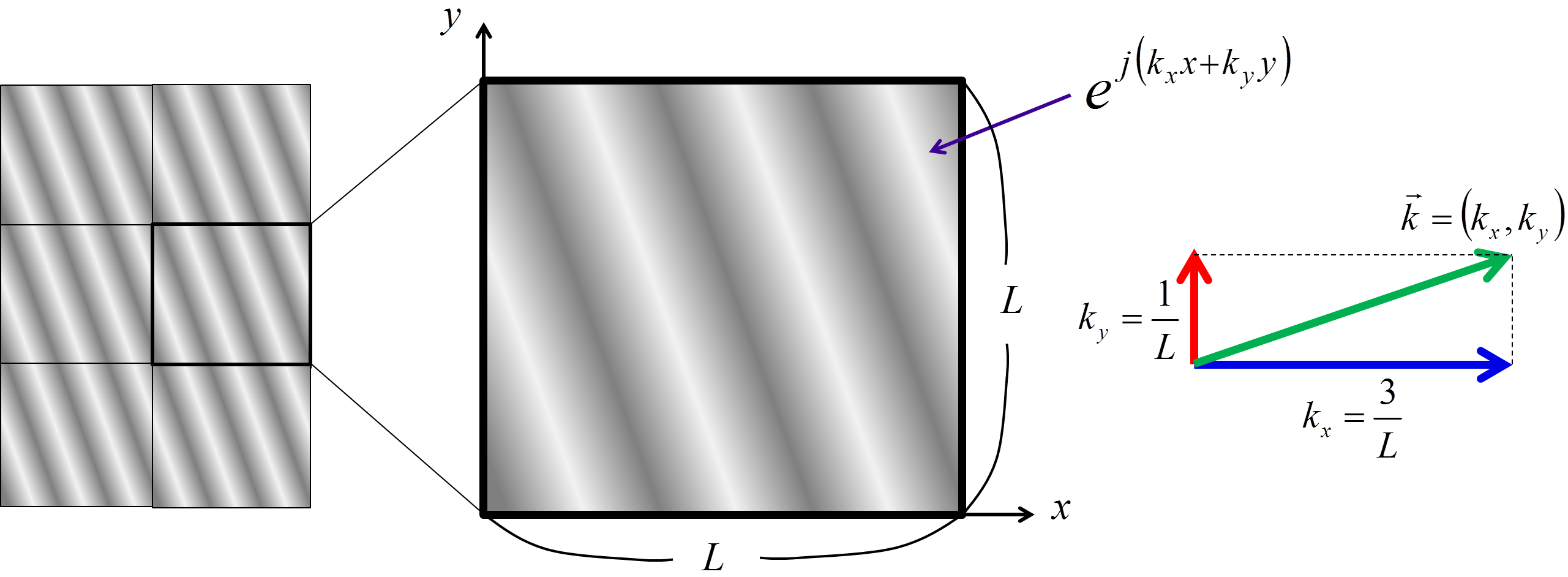
図6.周期的境界条件と定在波モードの数

 

　図6は2次元の定在波イメージである．\(L\times{L}\)の正方形における周期的境界条件というのは，真ん中に示した大きさ\(L\times{L}\)の正方形において，左境界と右境界はぴったり一致し，上境界と下境界もぴったり合わさることを言う．そのような定在波は，\(x\)方向の波数\(k_{x}\)（\(x\)軸方向の波長\(\lambda_{x}\)の逆数）と\(y\)方向の波数\(k_{y}\)（\(y\)軸方向の波長\(\lambda_{y}\)の逆数）がともに\(\frac{1}{L}\)の整数倍になればよいことがわかる．この図6に示した例では\(x\)方向に長さ\(L\)の間で3つの波が入り，\(y\)方向には長さ\(L\)の間に1つの波が入るので，

$$ \left(k_{x},k_{y}\right) = \left(\frac{3}{L},\frac{1}{L}\right) \tag{1} $$

と表される．一般化して，上記の周期的境界条件を満たす電磁波の波数は

$$ \left(k_{x},k_{y}\right) = \left(\frac{n_{x}}{L},\frac{n_{y}}{L}\right) \tag{2} $$

と表されねばならない．ただし，\(n_{x},n_{y}\)は共に整数である．同様にして3次元バージョンも考えてみよう．

 

図7.三次元の定在波モード

 

　3次元において周期的境界条件を満たす電磁波の波数は，同様に下記のように拡張される．

$$ \vec{k} = \left(k_{x},k_{y},k_{z}\right) = \left(\frac{n_{x}}{L},\frac{n_{y}}{L},\frac{n_{z}}{L}\right) \tag{3} $$

ここで，\(\vec{k}\)は波数ベクトルと呼ぶ．波数ベクトルの大きさ\(\left|\vec{k}\right|\)が大きいほど周波数が高い電磁波になることは言うまでもない．具体的に周波数\(\nu\)との関係を表すと，

$$ \nu = c\left|\vec{k}\right|\tag{4}$$

となる．この式（３）と式（４）から，周波数\(\nu\)を定在波モードを表す整数組\(n_{x},n_{y},n_{z}\)で表すと

$$ \nu = c\sqrt{k_{x}^{2}+k_{y}^{2}+k_{z}^{2}} = \frac{c}{L}\sqrt{n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}\tag{5}$$

と表される．ここまでくれば，周波数区間\([\nu,\nu+d\nu]\)の間に入る定在波の数が求められる．\(\frac{c}{L}<<\nu\)とすれば，周波数区間\([\nu,\nu+d\nu]\)の間に入る整数組\(\left(n_{x},n_{y},n_{z}\right)\)の数\(N^{'}\left(\nu\right)d\nu\)は

$$ N^{'}\left(\nu\right)d\nu =4\pi{\nu}^{2}\left( \frac{L}{c}\right)^{3}d\nu \tag{6}$$

ここで今対象にしている体積は\(V=L^{3}\)なので，上記の式（６）を単位体積当たりに変換し，偏波モード２つ分として2を掛けると，最終的に周波数区間\([\nu,\nu+d\nu]\)の間に入る定在波モードの数\(N\left(\nu\right)d\nu\)は

$$ N\left(\nu\right)d\nu =8\pi{\nu}^{2}\left( \frac{1}{c}\right)^{3}d\nu \tag{7}$$

となる．古典的には，この各電磁波モードにエネルギー\(k_{B}T\)が分配されたスペクトル強度が温度\(T\)の黒体輻射のスペクトルと考えられるが，実際はまったくそうはならない（長波長極限で正しいが）．実際には，量子的な効果を考える必要があるのだ．どういうことかというと，周波数\(\nu\)の電磁波モードは，エネルギーが\(h\nu\)の単位で離散化（量子化）されているのである．これは周波数\(\nu\)の光子１つのエネルギーが\(h\nu\)であると言い換えることもできる．ここで，例えば\(k_{B}T<<h\nu\)となる周波数\(\nu\)の定在波モードには，エネルギー\(k_{B}T\)を割り振ろうにもエネルギー単位の一口が\(k_{B}T\)をはるかに凌駕しているので，滅多なことではその周波数モードに光子1つすら加えることができない．結局光子のエネルギーが\(k_{B}T\)を超える周波数帯のスペクトル強度は指数的に小さくならざるを得ない．つまり1つの周波数モードにエネルギー\(k_{B}T\)が分配されるという高校物理で習った熱力学の話が，高周波領域では全く成り立たないことがすぐに理解できるだろう．周波数\(\nu\)のある1つの電磁波モードにいくつ光子が励起されるのか，その期待値\(\left<n_{\nu}\right>\)が分かれば，それに光子1つのエネルギー\(h\nu\)を掛けることでその電磁波モードにどれほどのエネルギーが割り当てられるのかを知ることができる．そして光子数の期待値\(\left<n_{\nu}\right>\)は統計力学の知見から次に示すボーズ・アインシュタイン分布に従うことが分かっている．

$$ \left<n_{\nu}\right> = \frac{1}{e^{\frac{h\nu}{k_{B}T}}-1} \tag{8} $$

これに光子1つのエネルギー\(h\nu\)を掛けることで，周波数\(\nu\)の１モード当たりのエネルギー\(E_{\nu}\)が求まる．

$$ E_{\nu} = \left<n_{\nu}\right>h\nu = \frac{h\nu}{e^{\frac{h\nu}{k_{B}T}}-1} \tag{9} $$

これに周波数区間\([\nu,\nu+d\nu]\)の間に入る定在波モードの数\(N\left(\nu\right)d\nu\)を掛けてやれば，周波数区間\([\nu,\nu+d\nu]\)の放射強度\(u\left(\nu\right)d\nu\)が求まる．つまり式（９）に式（７）を掛けてやって，

$$ u\left(\nu\right)d\nu = E_{\nu}N\left(\nu\right)d\nu = \frac{8\pi{h}{\nu}^{3}}{c^{3}\left(e^{\frac{h\nu}{k_{B}T}}-1\right)}d\nu \tag{10} $$

これでついに図4で示したスペクトル強度のグラフを導出できた．ただし図4は\(\lambda\)が横軸なので，式（１０）に\(\nu = \frac{c}{\lambda}\)を代入してやればよい．ここで\(d\nu = -\frac{c}{\lambda^{2}}d\lambda\)という変数変換と，エネルギー密度は常に符号が正になるように表示する点に注意されたい．

$$ u^{'}\left(\lambda\right)d\lambda = \frac{8\pi{h}c}{\lambda^{5}\left(e^{\frac{hc}{\lambda{k_{B}}T}}-1\right)}d\lambda \tag{11} $$

　この式（１０）や式（１１）から，電気機器工学などでもおなじみのウィーンの変位則とステファン・ボルツマンの法則も導ける．ウィーンの変位則というのは，この式（１１）のピークの波長\(\lambda_{m}\)が温度\(T\)に反比例するというものである．それはこの式（１１）を\(\lambda\)について微分してそれが0になるときの\(\lambda\)の値が温度\(T\)に反比例していることを示せばよい．

　また，ステファン・ボルツマンの法則は以下を示せばよい．

$$ \int_{0}^{\infty}u\left(\nu\right)d\nu \propto T^{4} \tag{12} $$

　これは純粋に数学の問題なのでここでの解説は割愛する．

　ともかく，なぜ熱放射が図4に示すようなスペクトルになるのか，その物理的な背景とその理論を一通り理解できたことと思う．次の記事では，この結果を用いて，白熱電球の実際のスペクトル強度分布などについて考察していく．

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス