誘導機の等価回路
まず結論から言ってしまおう.下記の図1が誘導機の等価回路である
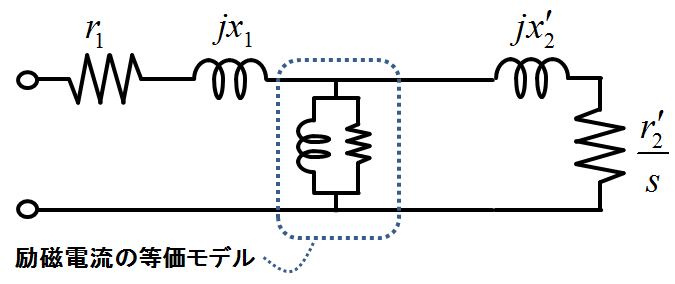
図1.誘導機の等価回路(星形換算1相分)
この図1に示す等価回路は2端子であるが,三相交流誘導機は3端子必要である.これは三相交流誘導機を星形換算した1相分の等価回路である(図4にて後述).ちなみに図中の\(s\)はすべりである.
この等価回路を用いれば,電気的な特性が表現できるので,実験などにより各パラメータ(\(r_{1},jx_{1},jx_{2}^{'},\frac{r_{2}^{'}}{s}\),それと励磁電流モデル)が特定できれば,一般のすべり\(s\)について消費電力や力率などを計算できるようになる.
この図1を用いると実際の計算上相当苦労する場合が多いので,通常手計算で用いるモデルは以下の図2の方である.
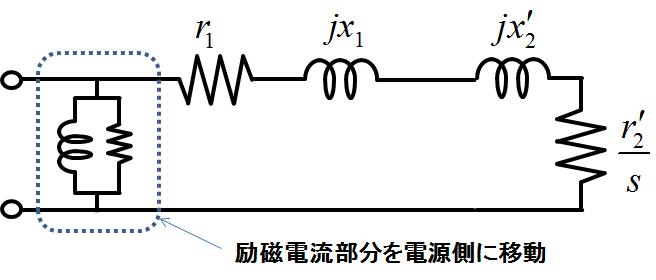
図2.誘導機のL型等価回路(星形換算1相分)
この図2の等価回路(L型)では励磁電流部分が電源側に引っ越している.これは,励磁電流が電機子電流全体に対して十分小さければ励磁電流の位置を変えても計算に大きな結果の差は出ないという考えの元に採用されている等価回路で,これを用いると計算が大変シンプルにできる.これは実際に読者がトルクなどの計算を紙と鉛筆で行う際に痛感することだろう.等価回路の形から,図1はT型等価回路,図2はL型等価回路などと呼ばれる.
これらの等価回路を使えば,消費(発生)電力や力率などの電気的特性だけでなく,機械的出力(入力)やトルク,効率なども計算できるようになる.具体的には,次に示す図3の等価回路を使う.

図3.機械的出力を求めやすい等価回路
この図3は,図2に示したL型等価回路の2次側の等価抵抗\(\frac{r_{2}^{'}}{s}\)を①と②の2つの抵抗に分割したものである.①での消費電力は2次側で実際に生じる銅損で,②の抵抗で消費する電力は機械的出力に等しい.このように,機械的出力と二次銅損の切り分けを,図3に示すような抵抗分割で表現することが可能なのである.なぜこのような切り分けができるのか,その物理的理由は後の記事で説明する.
次に,これらの等価回路と実際の三相交流誘導機との間の関係がどのようになっているのか,図4で示そう.
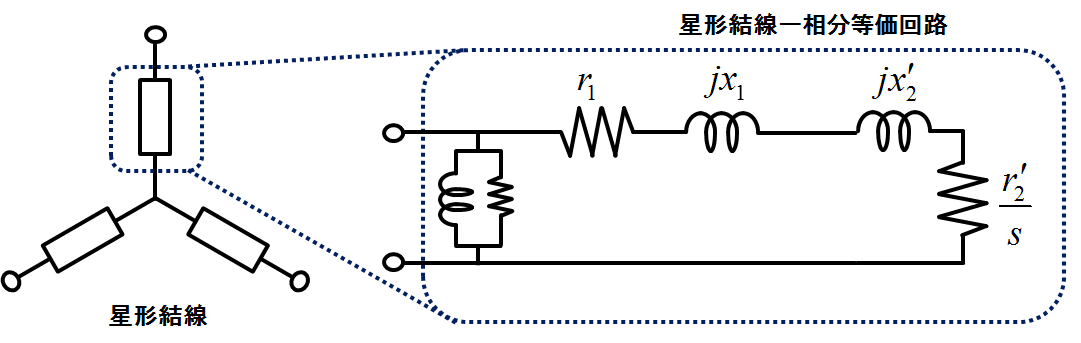
図4.星形換算1相分の意味
星形換算1相分の等価回路と言われれば,誘導機全体をY結線と考えたときの中性点から一端子までの等価回路部分を指す.つまり,この等価回路の消費(発生)電力や機械的出力(入力)を3倍したものが誘導機全体の値となる.ここで発電動作時はすべり\(s<0\)なので,等価回路の抵抗値は負になり,電力は消費ではなく発生となることを付け加えておく.
この項の最後に,誘導機の等価回路がなぜ図1~3のような形で表されるのか,その理由にここで少しだけ触れておこう.図5をご覧いいただきたい.
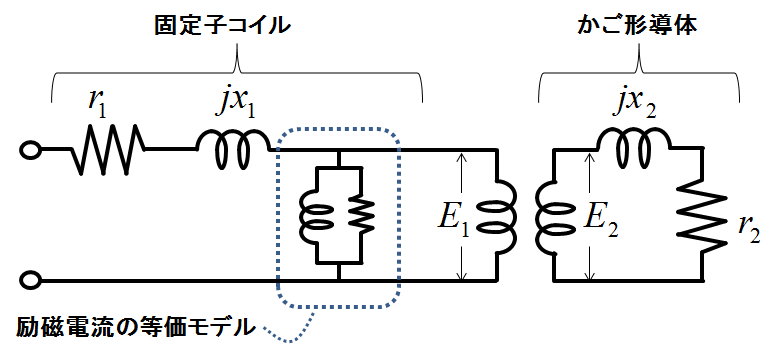
図5.誘導機の等価回路(変圧器を用いた表現)
次の記事でも説明するが,電磁気学的に見ると誘導機は実質的に変圧器と同じであるので,図5に示すような変圧器の等価回路がベースとなる.実際図1と図5はよく似ているだろう.固定子コイルが変圧器の1次側,かご形導体が2次側に対応している.
それでは早速次の記事においてこのイメージを詳しく解説していくことにしよう.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】のP.248~268にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











