誘導機の等価回路の物理的考察1(変圧器モデル)
前回の記事に少し登場した通り,誘導機の等価回路はほとんど変圧器の等価回路がベースになっているということをまず押さえておこう. 特に,誘導機のすべり\(s=1\)(回転子が静止)のときは,誘導機は変圧器そのものとなる.
それを踏まえると,まずすべり\(s=1\)(静止)のときの等価回路は以下の図1のように書ける.
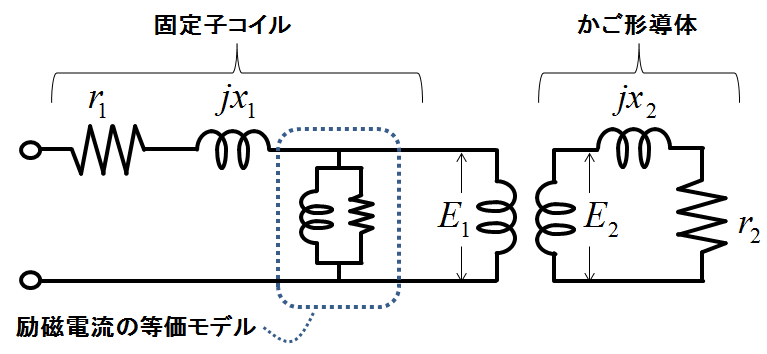
図1.静止している誘導機の等価モデル(変圧器モデル)
「静止している誘導機の等価回路など興味はない.回っているときの等価回路は?」という疑問は当然出てくるが,実は静止しているときの等価回路がわかれば,そこからちょっとした変更で回転している誘導機の等価回路も導き出せるのである.そのことは後述するとして,そもそも静止している誘導機がなぜ変圧器としてモデル化できるのか,次の図2で簡単に説明しよう.
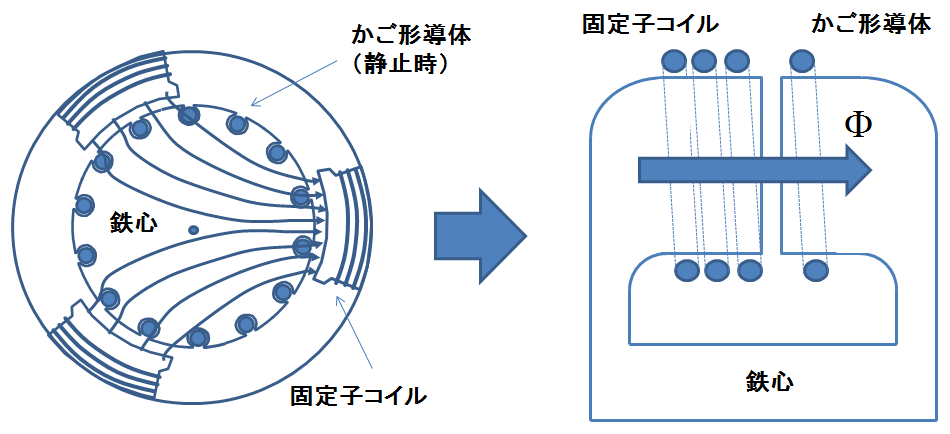
図2.静止している誘導機が変圧器でモデル化される訳
この図2の左側に示すように,固定子コイルが1次側,かご形導体が2次側として,この2つのコイル同士が鉄心を介して磁気的な結合をしているので,それは同図の右側のような形で表現ができる.この右側は変圧器そのものであることがわかるだろう.ということで,この記事では変圧器の等価回路がどのようになるのか,またなぜ図1のように表されるのか,をこれから説明して行くことにしよう.
次の図3に示すのは,もっとも単純な変圧器のモデルである.
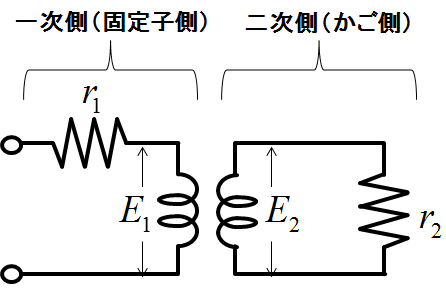
図3.漏れ磁束なしの場合
漏れ磁束がない場合は,導体の抵抗成分だけ考えればいいので図3のような等価回路が描けるのである.
しかし実際には次の図4に示すような漏れ磁束が存在する.
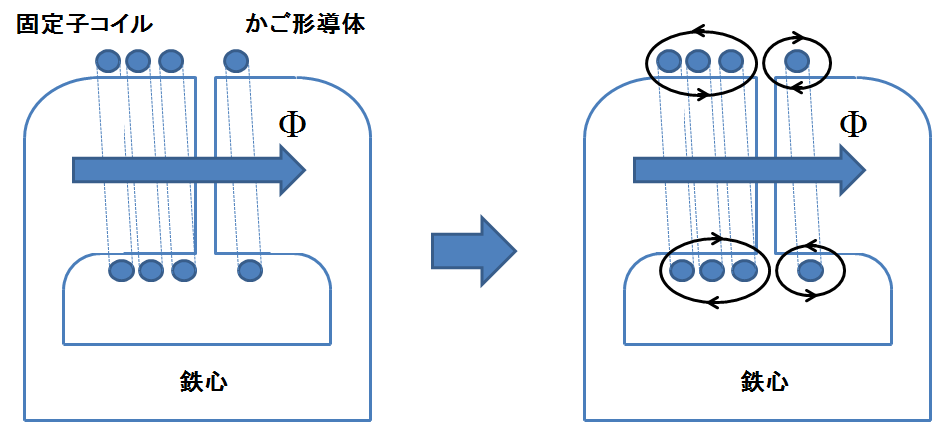
図4.漏れ磁束がない場合(左)とある場合(右)
漏れ磁束というのは,鉄心などを介した2つのコイルの共通磁気経路から外れた磁束のことで,図4の右側の黒いループで示した磁束のことである.
この漏れ磁束があることで,図3で示していたもっとも単純な変圧器のモデルは次の図5のように変更を受ける.
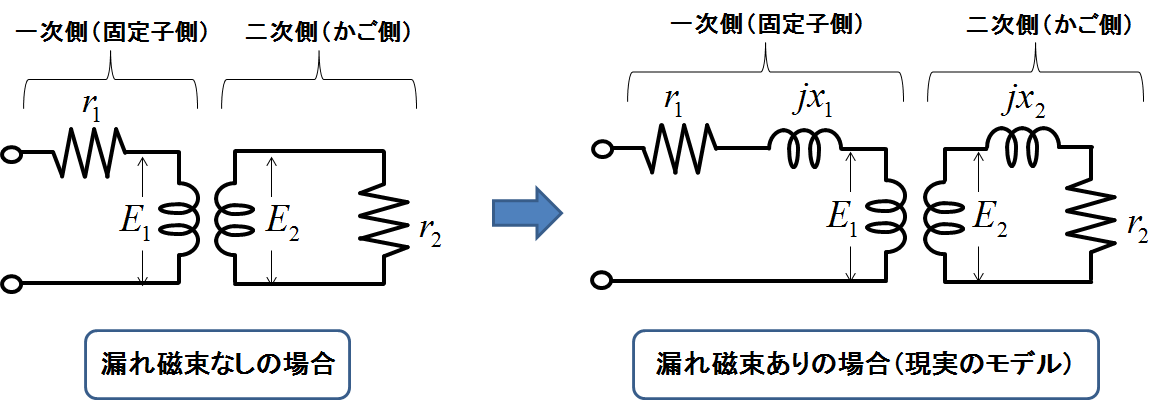
図5.漏れ磁束による変圧器等価回路の変化
実際の誘導機ではこの漏れ磁束によるインダクタを考慮しないと全く正確な等価回路にはならない.さらにこれに励磁電流の効果を入れることで,最初に示した典型的な変圧器のモデルである図1に帰着するのである.誘導機の等価回路を考える上で,この変圧器の等価回路を理解することは何よりも大事なので,上記はしっかり復習いただきたい.
この後,回転している誘導機の等価回路とその物理的理由が気になる方は次の記事を飛ばして”誘導機の等価回路の物理的考察2(近日中Up)”を,その前に誘導機の励磁電流の等価回路を考察したい人は次の記事”誘導機の等価回路の物理的考察3(近日中Up)”を,それぞれ参照いただくとよいだろう.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】のP.248~P.268にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











