同期機のベクトル図と機械的出力(入力)
まず,下の図1は何を示しているのかわかるだろうか.
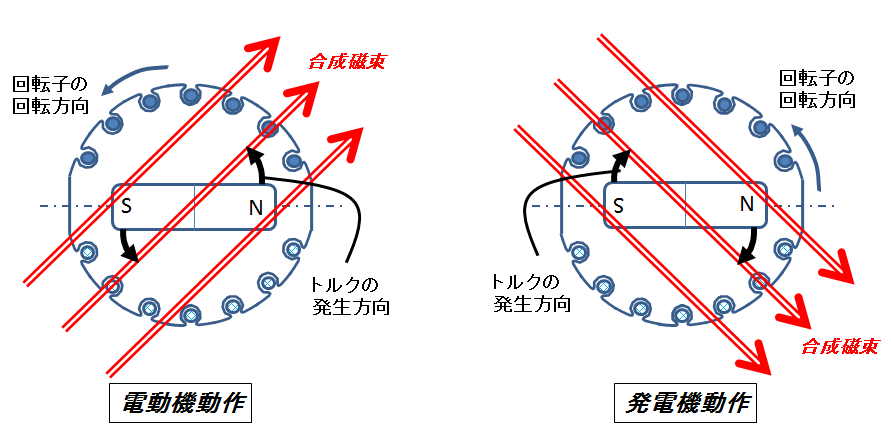
図1.合成磁束の向きと電動機・発電機動作
これは,反時計回りに回っている回転子に対して合成磁束がさらに反時計回りに進んでいれば電動機動作,逆に回転子から合成磁束が時計回りに遅れていれば発電機動作,ということを示している.勿論回転子と合成磁束は同じ回転速度で反時計回りに回っており,回転子から見た合成磁束の相対的な角度が進んでいるのか遅れているのか,という違いを表している.同図左側は現にトルクが回転方向に働いているので,電気の力が回転を助けている(電動機として働いている)ことがうかがえる.また,同図右側は逆に回転方向と逆にトルクが働いているので,電気の力が回転を妨げている(発電機として働いている)ことがわかる.
これがベクトル図でどのように対応するのか,次の図2で見てみよう.
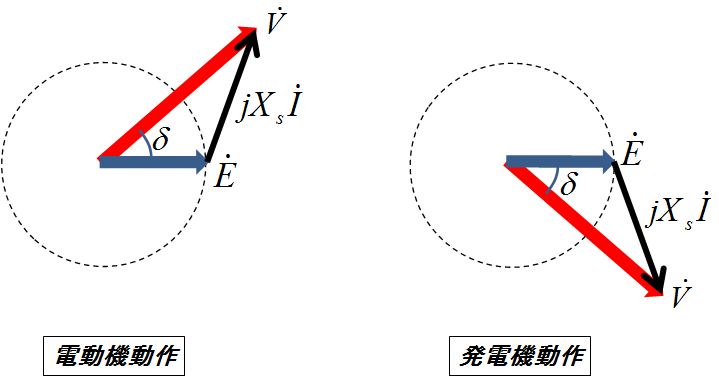
図2.ベクトル図と電動機・発電機動作
電動機動作のとき(左側)は端子電圧\(\dot{V}\)が起電力\(\dot{E}\)よりも位相が進んでおり,発電機動作のとき(右側)は逆に端子電圧 \(\dot{V}\)が起電力\(\dot{E}\)よりも位相が遅れている.発電機動作時のベクトル図においては,電機子電流\(\dot{I}\)の符号の向きを同期機から出る向きをプラスに取る場合が一般的なので,そのときは右側の電流の矢印(黒)の向きは逆になる.(今回は両方の電流の向きの定義を揃えている)
次に負荷角の大きさで,トルクがどのように変わるのか,まずは直感的に考察してみよう.下記の図3をみていただきたい.
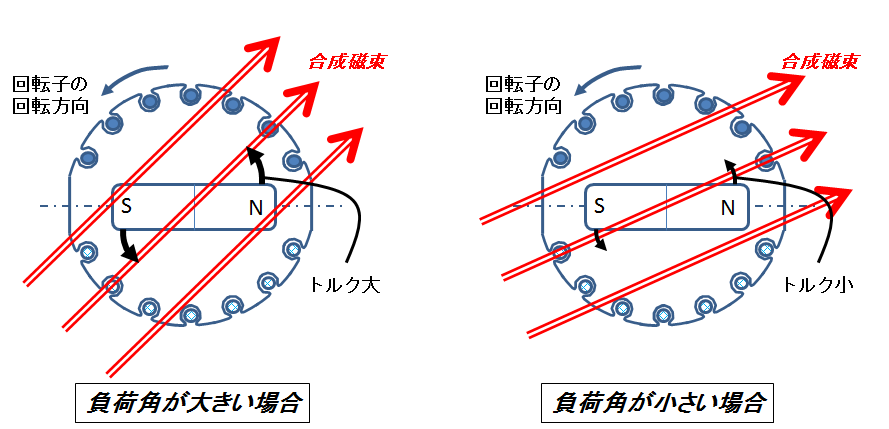
図3.負荷角の大きさとトルク
回転子は巻線形であろうが永久磁石形であろうが,磁石であることに変わりないので,合成磁束との角度(負荷角)が増せば増すほどトルクは大きくなることが想像できるだろう.左は負荷角が大きい場合,右は負荷角が小さい場合を表している.次はこの状況をベクトル図に対応させるとどのようになるのか,下の図4に示した.
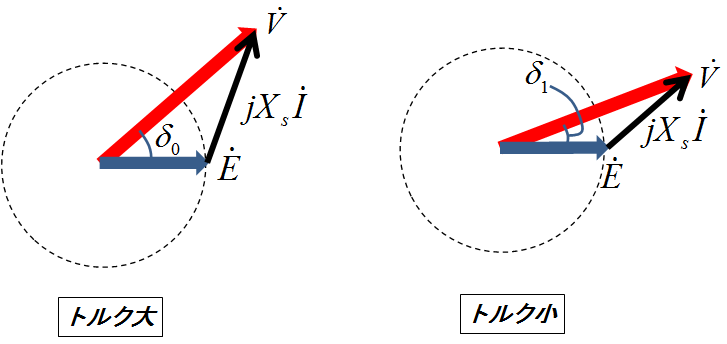
図4.ベクトル図における負荷角の大きさとトルク
これまでの記事でも理由は何度か触れたが,負荷角はベクトル図上においては端子電圧\(\dot{V}\)と起電力\(\dot{E}\)とのなす角のことである.同じ電動機での比較ならば(\(\dot{X_s}\)が同じならば),左は負荷角\(\delta_0\)が大きいのでトルク大,右は負荷角\(\delta_1\)が小さいのでトルク小と言える.また,起電力\(\dot{E}\)が大きくなれば(回転子の電磁石が強くなれば)トルクは大きくなるし,端子電圧\(\dot{V}\)が大きくなっても(回転磁束が強くなっても)トルクは大きくなるはずなので,トルクないしは機械的出力はこれらのベクトル図の三角形の面積に比例しそうである.実際その直感が正しいことを,下記の図5を題材にして,数式の上でも示していくことにしよう.
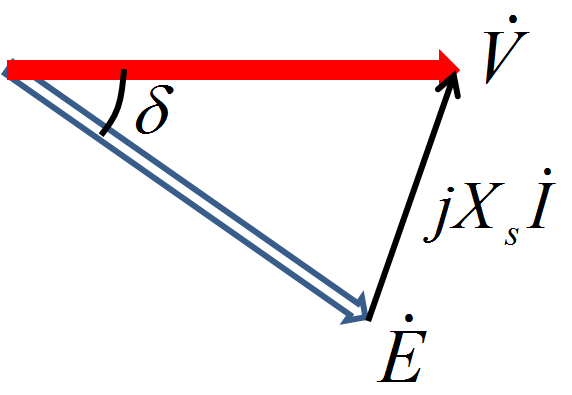
図5.ベクトル図の1例(電動機動作時)
このベクトル図の面積を扱いたいので,とりあえず図6のように赤い辺に垂線を下してみる.
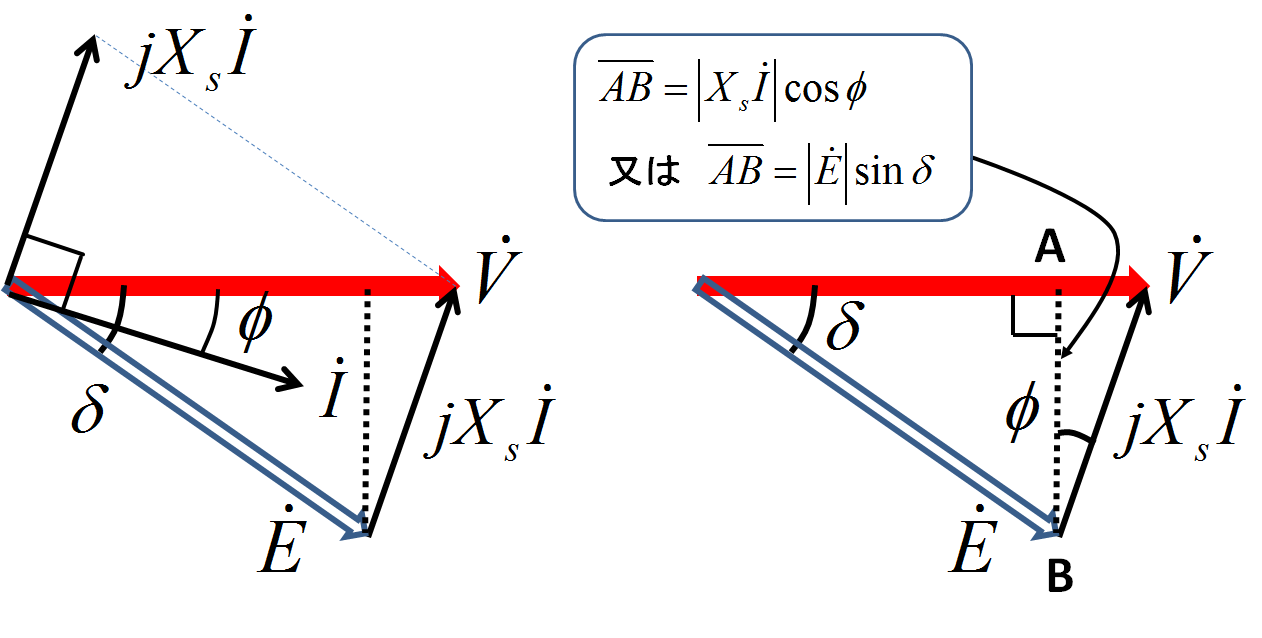
図6.ベクトル図の三角形の面積を求める図
すると,図中にも示したが,垂線ABの長さは,力率角\(\phi\)を利用して
と表すことができる.三角形の面積\(S\)はこれに底辺の長さ\(\left | \dot{V} \right |\)を掛けて\(2\)で除したものなので,
ここでベクトル図の電圧や電流の絶対値は1相分のそれと同じであるということを思い出せば,今回電圧や電流が実効値であるとして\(IV\cos\phi\)は1相分の消費有効電力に等しくなる.すると電動機全体の機械的出力\(P_m\)はその\(3\)倍で,
式(2)と式(3)から
確かに機械的出力\(P_m\)はベクトル図における三角形の面積\(S\)に比例している.この三角形の面積\(S\)は高校数学の知識があれば,負荷角\(\delta\)を用いて次のように表すこともできる.
式(4)に式(5)を代入すれば,
これがベクトル図から導かれる機械的出力を表す式である.この数式を負荷角 を横軸にとって図示すると下記の左側のようなグラフになる.
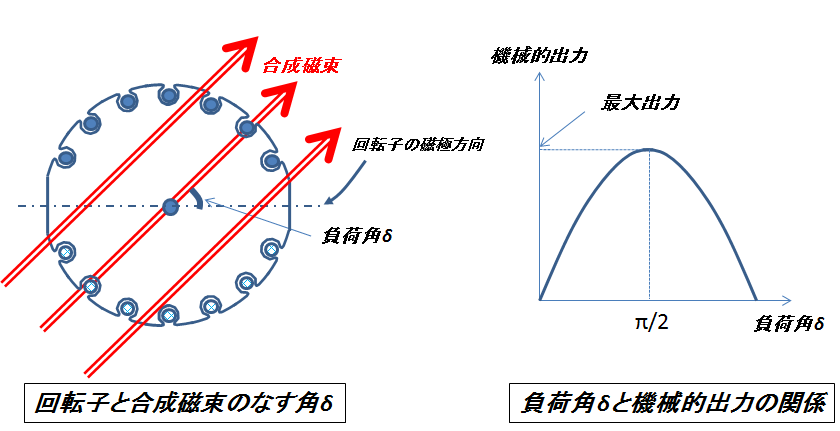
図7.負荷角と機械的出力の関係
グラフの形は式(6)に示したように正弦波の形となっており,負荷角\(90^\circ\)を境に機械的出力が減少に転じる様子が見て取れる.次の記事では同期発電機について有効電力や無効電力の発生量とベクトル図との関係を明らかにしていこう.
この項の内容に関する,より詳細で完全な解説は,
【徹底解説 電動機・発電機の理論】のP.163~P.165にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.











