誘導機の等価回路の物理的考察３（回転系）

　（誘導機の等価回路の意味が理解できている方は次の記事に飛んで構いません．）

　これまでは「静止している」誘導機の等価回路を考えてきたが，ここで遂に「回転している」誘導機を扱っていくことにしよう．いきなり難易度が増すイメージがあるが，実は静止しているときの物理をしっかり復習しながら考察を勧めれば，回転しているときの物理的状況もすんなり理解できるのである．早速考察に入ろう．

　まずここで，「静止している」ときの誘導機のモデルを図1にて思い出そう．

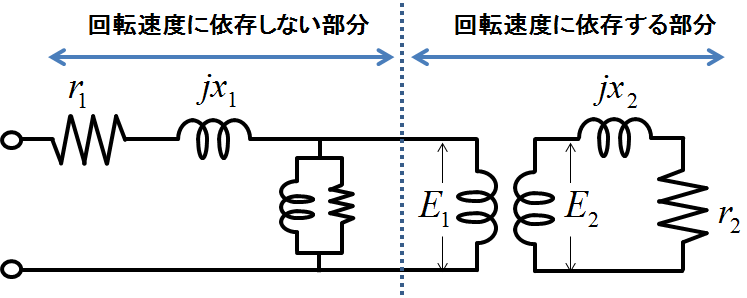
図1.静止しているときの誘導機の等価回路

　この図1は，静止しているときの誘導機の等価回路（１相分）であり，変圧器の等価回路そのものであった．誘導機が回転を始めると，この等価回路はどのように変更を受けるだろうか．まず簡単に予想を立てるならば，図1のうち点線の左側は全く変更を受けないはずである．なぜならば固定子コイル側に対応する回路部分であったり，励磁電流の等価回路部分だったりするので，これらは回転子が回転しているか否かで結果は変わらないはずだからである．変わるとすれば点線の右側，つまりかご形導体との磁気的結合を表す部分と予想できるだろう．

　最初に答えを言ってしまうと，回転により変化する等価回路部分は下記の図2中のピンクで示した抵抗値が変更を受ける．

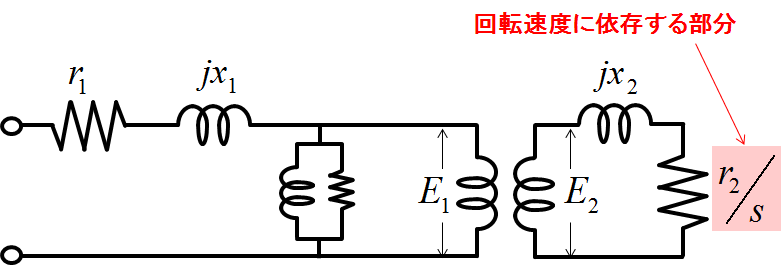
図2.回転しているときの誘導機の等価回路

　なぜこのような簡単な変更で済むのか．回転子が回っていては，もはや変圧器と呼ぶことはできないのではないだろうか．２次側コイルが１次側コイルに対して動いている変圧器とは，一体何者なのだろうか？

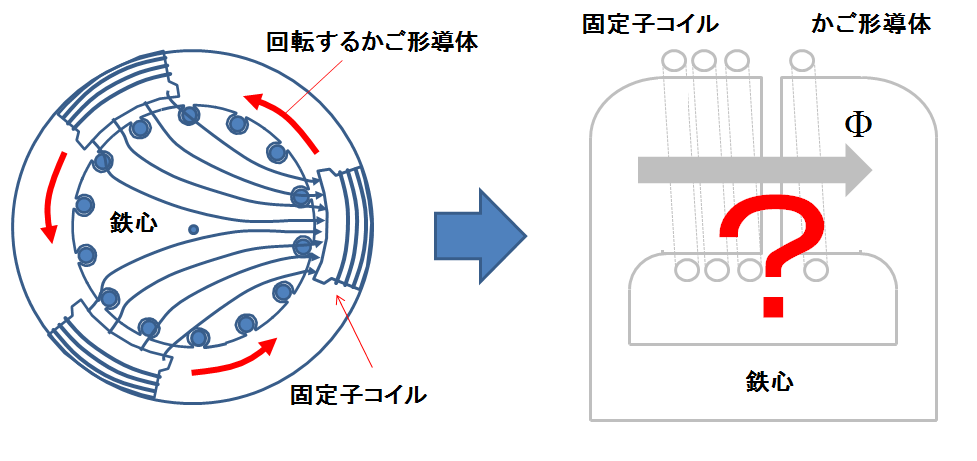
図3.誘導機が回転しているときは変圧器ではない？

　この疑問に答えられたときに初めて，図2の等価回路の意味を真に理解したと言える．ということで，この疑問をこれから徹底的に（しかし直感的に）突っ込んで考えてみることにする．

　これも結論から言ってしまうと，静止しているときの変圧器をそのまま使うことができるのである．回転子が回転していようがいまいが１次側（固定子コイル）と2次側（かご形導体）の磁気的結合の強さは変わらないからである．つまり，変流比は回転速度によらない．よって，２次側（かご形導体）に流れる電流の変化がわかれば同じ変圧器を用いて一次側（固定子コイル）に流れる電流も計算できる．それでは２次側の電流とはどんなものであったか？回転を始めると次の図4に示すように，２次側のかご形導体に流れる誘導電流の分布（$\theta$や電流の強さ）が変化することは以前の記事で紹介した．

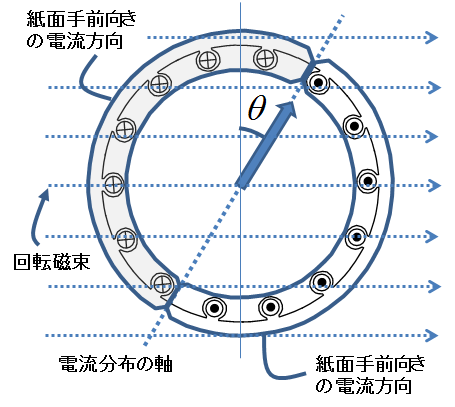
図4.静止時の変圧器を等価回路に使える理由（誘導電流分布）

　この誘導電流分布は回転磁束を基準に取ると静止している．言い方を変えれば，かご形導体の誘導電流は固定子から見たら同期回転速度（回転磁界の回転速度）と同一になる．この誘導電流分布の変化（要するに２次側電流）が求まれば，等価回路は求まったも同然となる．それでは２次側に流れる誘導電流が，任意のすべり$s$についてどのように求まるか，次の図5で考えてみよう．

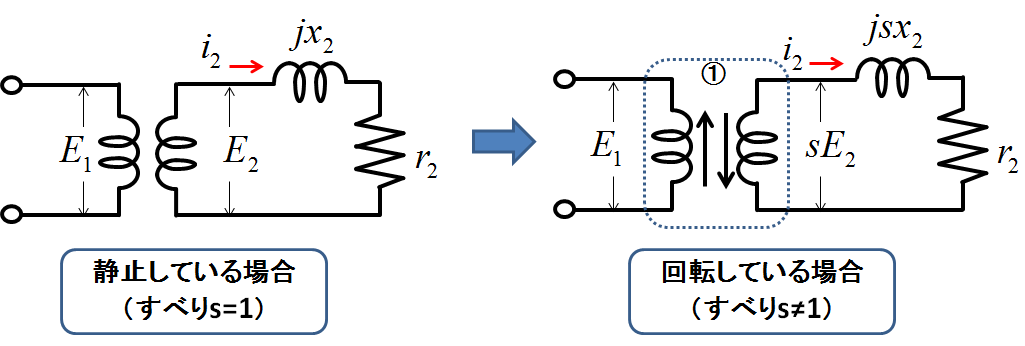
図5.2次側電流のすべり$s$依存性

　すべりが$s$の場合，かご形導体に発生する起電力は静止時（$s=1$のとき）に比べ$s$倍になる．そしてかご形導体に発生する誘導電流の周波数も$s$倍になるので，インダクタのリアクタンスは$x_{2}$から$sx_{2}$に変更される．ということは，ここに流れる誘導電流$i_{2}$は次のようになる：

$$i_{2} = \frac{sE_{2}}{jsx_{2}+r_{2}} \tag{1}$$

　今までの話を総合すると，上記の式（１）と同一の２次側電流を流しながら，静止時の変圧器をそのまま用いるという等価回路こそ，すべり$s$のときの誘導機の等価回路となる．その両方の条件を満たす変換は次の図6である．

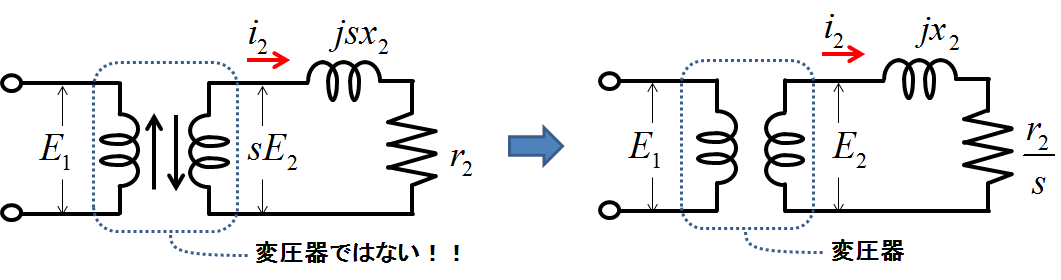
図6.静止時の変圧器を用いた等価回路の表現

　元の変圧器を用いようと思ったら，２次側の電圧は$sE_{2}$ではなく$E_{2}$であるべきである．一方で２次側電流$i_{2}$は式（１）で示した通りになるべきである．それを満たすためには，すべり$s$のときの２次側リアクタンス$sx_{2}$と抵抗$r_{2}$をそれぞれ$s$で割ればよい．

　要点をまとめよう．

　１．回転していようがいまいが，同じ変流比の変圧器で表される．（鉄心が回っていようが磁気的結合は変わらない）

　２．すべり$s$によりかご形導体に流れる誘導電流$i_{2}$は式（１）のように表される．

　３．静止時と同じ変圧器で，２次側電流が式（１）のようになる等価回路が，求める等価回路である．

　等価回路の物理的イメージが湧いただろうか？次の記事からは，この等価回路を用いて誘導機の諸特性を分析したり，それらを直感的に示す円線図などの紹介をしていく．

この項の内容に関する，より詳細で完全な解説は，

【徹底解説　電動機・発電機の理論】のP.248～268にて展開されています．是非ご参照を!!