直流電動機のトルク

 

　直流機のトルク計算をする際に，余り複雑な例にいきなり挑んでも怪我をするだけなので，下記の左側の図に示したような，最もシンプルな整流子型直流電動機（図1）を例にとってトルクの計算をしていこう．

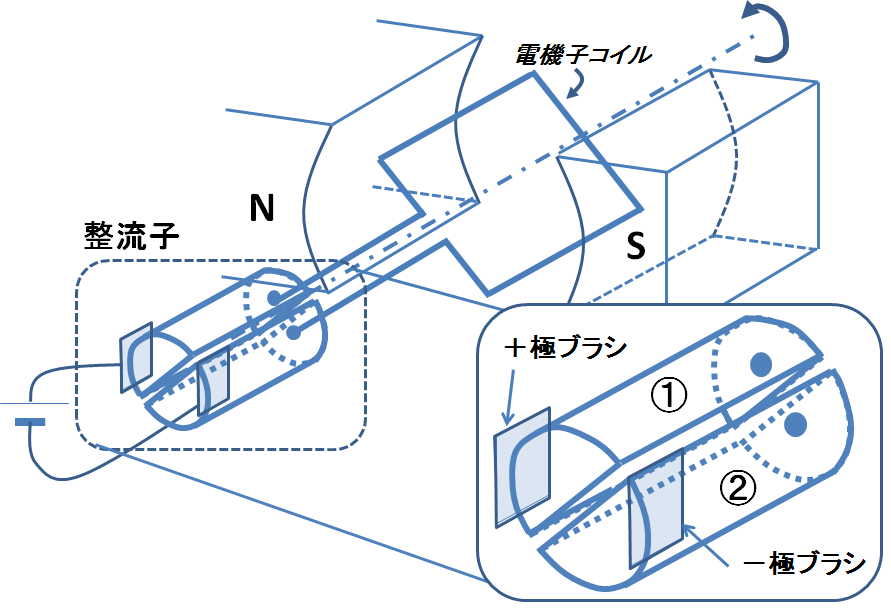
図1.整流子型直流電動機

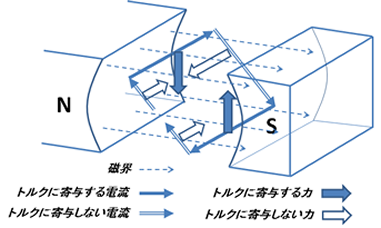
図2.導線に働く磁気的な力


 

　図1に示した整流子型直流電動機は，導線が4辺あるが，この4辺ともに磁場中で電流を流しているので，それぞれ電磁力が働いている．フレミングの左手の法則を用いれば，それぞれの４辺に働く力は，右の図2のように求めることができる．ここで，青く塗られた太い矢印はトルク（回転力）に寄与する力，一方白抜きの太い矢印はトルクに寄与しない力である．つまり，トルクを計算したいだけならば，回転軸に平行な２本の導線を抜き出して議論すればよい．実際にトルクに寄与する導線部分のみを抜き出した直流電動機の模式図を下の図3に示してみよう．

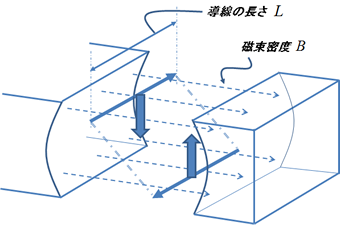
図3.トルクに寄与する導線部分

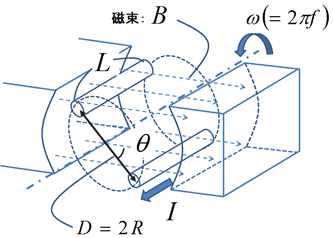
図4.トルク計算のためのパラメータ


 

　図3のように，回転軸に平行な導線のみがトルクに寄与する導線部分になる．つまりこの導体に働く力がわかれば，トルクは求められる．そこで右の図4のように，トルクを求めるために必要なパラメータを定義しておく．

（角速度\(\omega\)についてはトルクを求めるときには必要なく，誘導起電力を求めるときに必要となる．）

　図4で与えた文字を用いて，トルクを早速計算してみよう．まず計算しやすいように図4を下記の図5のように書き換えてみる．

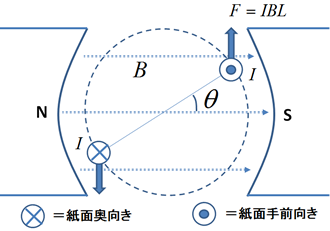
図5.トルク計算のための断面図

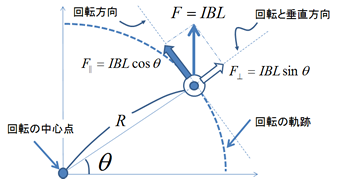
図6.トルク計算の考え方


 

　図5は回転軸と垂直な面で電動機を切った様子を表している．右上の導線は上に，左下の導線は下に，それぞれ力が働いているので，この電動機は反時計回りにトルクが生じているだろう．トルクを求めるためには，導線に働く力の大きさ\(F\)を知る必要がある．高校物理の教科書を見返してみれば，電流\(I\)を流す長さ\(L\)の導線が磁束密度\(B\)中で受ける力の大きさ\(F\)は以下のように表されることがわかるだろう．

$$F=IBL \tag{1}$$

　上記の図5の2つの導線に働く力は式（1）の通りなので，あとはそこから回転力に関係する成分だけ抜き出してあげればトルクが計算できる．回転に寄与する力の成分というのは，図6に示した通り，円の接線方向の力の成分である．つまり\(F_{||}\)で示されている力のことだ．その値は簡単な三角関数の計算により，\(IBL\cos\theta\)であるとわかる．ここまでくれば，トルク計算のゴールは目前である．トルクの定義を思い出すと，「回転方向の力の大きさ\(F_{||}\)とその力が働いている点の中心からの距離\(R\)の積」であった．さらに今回は導線が２本あるので，結局トルク\(T\)は，

$$T=2RF_{||}=2RIBL\cos\theta \tag{2}$$

と表すことができる．これにて図1に示したもっとも単純な直流電動機のトルクは計算することができたと言いたいところだが，まだここで一つ忘れていることがある．それは，この式が成り立つの範囲は，\(0\leq \theta \leq \frac{\pi }{2}\) であるということである．どういうことか，まずはこの式（2）のトルクを回転角度\(\theta\)を横軸にとって何周期分かプロットしてみよう．下の図7を見て頂きたい．

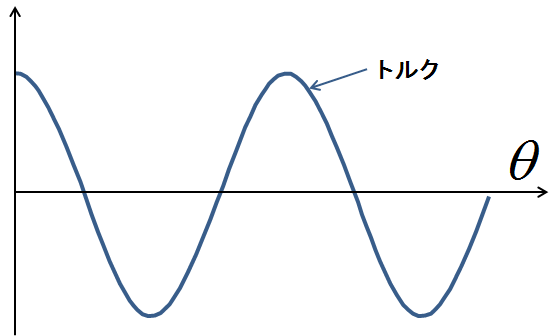
図7.整流子を考慮に入れないときのトルク

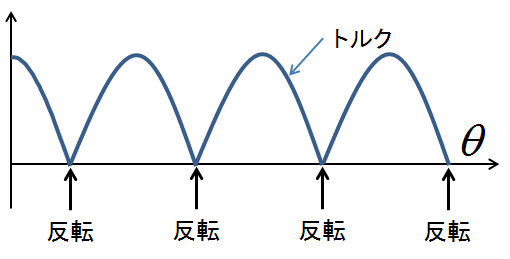
図8.整流子を考慮に入れたトルク


 

　まず図7を見ると，トルクが半回転するごとに正負逆転しており，一方向に定まったトルクではないことがわかる．これでは勿論正常な回転は望めない．というか，そもそもその状況を避けるために，整流子を使って半周回転（2極の場合）ごとに電流を反転させ，常に一つの方向にトルクを発生させるように工夫していたのだった．それを思い出すと，図7で示したトルクのグラフは，図8のように変更されることがわかる．つまり，整流子の効果によって図7のトルクを常に一定の方向に（ここでは正の符号に）折り返したようなグラフが，実際の直流電動機で発揮されるトルクのグラフになると言えるだろう．

　すなわち，式（2）で解けたと思っていたトルクの計算に整流子の効果を入れると，下記の（3）の形になる．

$$T=2RF_{||}=2RIBL\left | \cos\theta\right | \tag{3}$$

式（2）の絶対値に当たる式（3）が，図1で示したもっとも単純な直流電動機におけるトルクの計算結果となる．

　しかしこの結果は回転角度\(\theta\)において導体に発生する瞬間的なトルクであった．一方で我々が必要としているトルクは，この時間平均であろう．つまり，下記の図9における\(\overline{T}\)が必要になる．

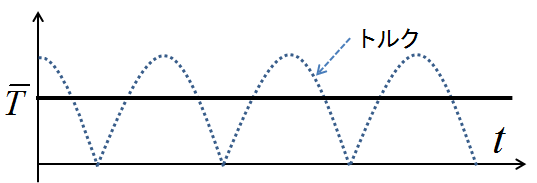
図9.トルク計算のための断面図

 

　ここで，横軸は\(\theta\)から時間\(t\)に変更した．定速で回転している分にはこの置き換えにより横方向のスケールが変わるだけである．求めたいのは時間平均だが，計算しやすいのは\(\theta\)上での平均だろう．定速で回転していれば両者の平均は同じなので，今回は\(\theta\)上で式（3）の平均を取ってみる．

$$\begin{eqnarray*} \overline{T}=\frac{1}{\frac{\pi}{2}}\int_{0}^{\frac{\pi}{2}}Td\theta &=&\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}2RIBL\left | \cos\theta \right |d\theta\\ &=&\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}2RIBL\cos\theta d\theta\\ &=&\frac{4RIBL}{\pi} \tag{4} \end{eqnarray*}$$

　回転角度\(\theta\)の依存性が消えて，定数になった．このようにトルクを時間について平均化した定数として扱っていい理由としては，はずみ車効果による慣性力や，回転速度が負荷変動の時定数よりも十分速いことなどが挙げられるが，何よりも重要なイメージとしては，以下の図10があるだろう．

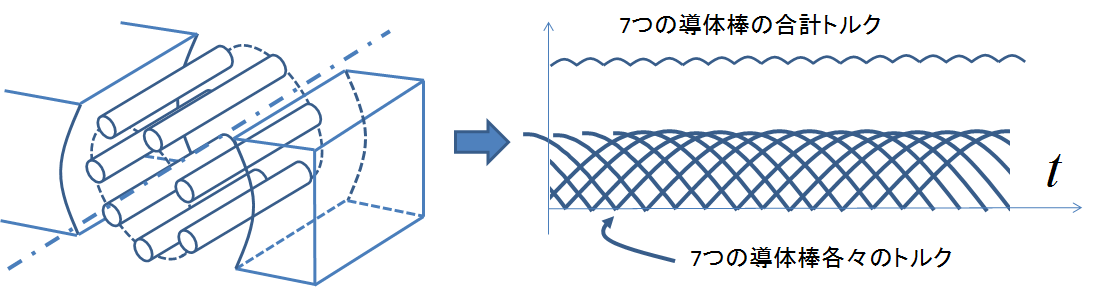
図10.分布的に導体数が増えた電動機のトルク

 

　このように分布的に導体の本数が増えた場合は，少しずつ位相のずれたトルクを足し合わせることで全体としてトルク変動が少ない電動機を構成することができる．この場合は，電流を流す導体1本当たり，式（4）で示した値の半分のトルクが寄与しているといえる．（式（4）は導体2本分の結果なので）

　ここで，式（4）は磁束密度\(B\)を用いて表しているが，この磁束密度\(B\)は形状依存により場所によって大きくその値が異なるので，大変扱いにくいものである．例えば，磁束密度\(B\)は回転位置\(\theta\)の関数であると考えられるのである意味\(B(\theta)\)と考えることができるわけだが，この関数\(B(\theta)\)の詳細がわからないと，式（4）の値も分からないということになり，大変不便である．そこで一般的には，磁極1つ当たりの磁束\(\Phi\)でトルクを表すということをする．式（4）の積分を，磁束密度\(B(\theta)\)として積分をやりなおすことにより磁束\(\Phi\)で表してみよう．

$$\begin{eqnarray*} \overline{T}=\frac{1}{\frac{\pi}{2}}\int_{0}^{\frac{\pi}{2}}Td\theta &=&\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}2RIB(\theta)L\left | \cos\theta \right |d\theta\\ &=&\frac{4I}{\pi}\int_{0}^{\frac{\pi}{2}}B(\theta)RL\cos\theta d\theta\\ &=&\frac{4I}{\pi}\cdot\frac{\Phi}{2}\\ &=&\frac{2I\Phi}{\pi} \tag{5} \end{eqnarray*}$$

　これで，磁束密度\(B\)が回転角度\(\theta\)に依存していようとも，1極当たりの磁束\(\Phi\)でトルクを表すことができた．これが，図1に記したもっとも単純な直流電動機のトルクの最終的な答えとなる．上記の2行目から3行目への積分は，著書の§3-2の演習問題において図形的に説明されているが，これは1/4周分の導体の軌跡で作られる面上における磁束密度の面積分となるので，その積分の値は1極当たりの磁束\(\Phi\)の丁度半分となる．これにより，磁束密度分布によらず，1極当たりの磁束でトルクを表すことができた．図1は導体が2本あったので，導体1本当たりの発生トルク\(\overline{T_1}\)は下記のように表すことができる．

$$\overline{T_1}=\frac{I\Phi}{\pi} \tag{6}$$

 

　ここまでで直流機のトルク計算の基本的説明は終了である．トルク計算のイメージはつかめただろうか．実際には並列回路数や総導体数，極数などにより，上記に示したトルクの結果は変化する．ただし，使う物理法則と解析のアプローチは常に上記の説明と共通である．

 

 

 

この項の内容に関する，より詳細で完全な解説は，【徹底解説　電動機・発電機の理論】のP.80～P.94にて展開されています．
是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス