共振形インバータ(入門編)

 

　本記事では共振形インバータの概要について説明していきたい．この記事を書くにあたり，主眼点をどこに置こうか，若干の迷いがあった．なぜなら，共振形インバータと一口に言っても，その使い道としてはDC-DC変換器用途，照明機器用途，誘導加熱用途，などいろいろ考えられ，また共振形インバータ採用のモチベーションの一つとして，ソフトスイッチングという手法があるのだが，この理論を解説したい思いもあったからである．要するに語られるべきポイントが多すぎて，要点をすべて一つの記事に集約することは難しいと言わざるを得なかった．いろいろ考えた結果として，この記事では「共振形インバータの物理的本質だけをとにかく丁寧に伝えよう」という方針に落ち着いた．
　なお，共振形インバータの応用例などについては，次の記事にて，簡潔に説明できる範囲の紹介をしていくこととする．とにかく本記事では，共振という現象自身について，時間ドメインでのイメージをしっかり身に付けていただければと思う．

 

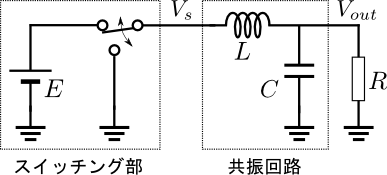
図1.一般的な共振形インバータ（並列共振形）

 

 

　

まず理解の対象となる共振形インバータの一例を図1に示す．どの共振形インバータについてもいえることだが，LとCによる共振回路に周期的な電圧を与え，共振回路の電圧ないしは電流を振動させるという方式を取る．この共振を駆動する部分が図1左側，スイッチング部である．この共振の原理を力学系に喩えて説明していこう．図2をご覧いただきたい．

 

 

図2.共振とはそもそも何だったか

 

 

図2左側は，外から力を加えられていない振り子が自由振動している様子を表し，同図右側はこの振り子の振幅が増大するように外から周期的な力を与えた場合を表している．共振形インバータのイメージは，外から周期的な力が与えられながら共振回路が振動しているということで図2右側に対応している．加えられる周期的な力の周波数は共振周波数に十分近くなければ有効な共振は生じない．逆に共振周波数に等しい周波数の力を与えれば，その力が非常にわずかであっても大きな共振を起こすことができる．このイメージを分かりやすく表している波形を図3に示そう．

 

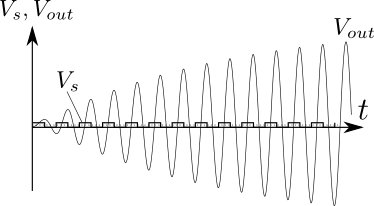
図3.図1の共振形インバータの共振が始まる様子

 

 

この波形は，図1に示した共振形インバータが共振を開始するときの電圧波形を表している．スイッチング部からLC共振回路に与えられる電圧\(V_{s}\)が小さかったとしても，共振回路の出力電圧であり負荷\(R\)に与えられる電圧\(V_{out}\)の振幅はどんどん大きくなっていく．この共振回路の損失が一切無ければ，共振周波数とスイッチング周波数が完全に一致している場合この振幅は際限なく大きくなっていくのだが，実際の共振系にはロスがあるので，図4に示すようにあるところで振幅が飽和する．

 

 

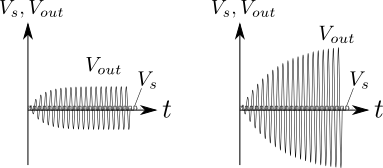
図4.\(Q\)値が低い場合（左）と\(Q\)値が高い場合（右）

 

 

共振回路のロスの大小は\(Q\)値（Quality factor）と呼ばれる値で表され，\(Q\)値が高い方がロスが小さく理想的な共振系であることを示している．図4に当てはめると，図4左側では振動が比較的小さい振幅ですぐに落ち着いているので\(Q\)値は低く，一方同図右側では同じ入力電圧\(V_{s}\)であるにもかかわらず出力電圧\(V_{out}\)の振幅はどんどん大きくなっていき，振幅が落ち着くまで比較的長い時間がかかっているので\(Q\)値は高い．もちろん\(Q\)値が高い方が小さな外力で大きく揺れてくれるし，入力がノイズだらけの矩形波でも出力はガタツキの小さいほとんど完璧なサイン波になるのでうれしいように感じるが，用途によっては必ずしもそうとは言えない．\(Q\)値が高いと，共振周波数からのずれがほんの少しでもあると共振しなかったり（ゲインが小さかったり），また発振器として用いる場合，その発振が安定するまで長い時間かかったりするので，この辺りが設計にとって致命的になる場合には無闇に高い\(Q\)値の共振回路を組むことはできない．

　また，共振形インバータにおいては共振回路の\(Q\)値が負荷のインピーダンスにより大きく変化する．例えば，図1の共振形インバータの場合，負荷の抵抗\(R\)が共振周波数（角周波数\(\omega_{res}\)）におけるキャパシタやインダクタのインピーダンス（\(\frac{1}{j\omega{C}},j\omega{L}\)）よりも十分高インピーダンスでなければ，\(Q\)値は高くならない．図1の共振形インバータの\(Q\)は

$$Q=\frac{R}{j\omega_{res}{L}}=j\omega_{res}{C}{R} \tag{1}$$

というように，負荷のインピーダンスと共振回路のLやCのインピーダンスの比で表される．共振形インバータの\(Q\)値は負荷のインピーダンス\(R\)により直接影響を受けるのである．ということは，「負荷のインピーダンスによって最適な共振回路の構成も変わるだろう」という予想がつく．そこで図5では，共振インバータの共振回路部分として代表的な3つのトポロジーを紹介しよう．

 

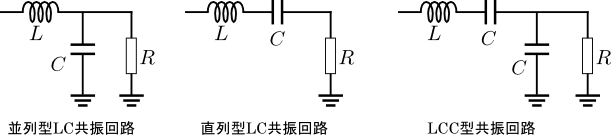
図5.LC並列共振回路, LC直列共振回路，LCC共振回路

 

 

今回主に説明したのは図5左側に示す並列共振形と呼ばれるタイプで，負荷の抵抗値\(R\)が大きい場合に採用される．試しに並列共振形の構成で\(R\)が非常に大きい状況を考えると，実質抵抗が存在しない状況と見ることができ，単なるLCのみの共振回路と等価になるため元気に共振するはずである．一方でこの並列共振形は抵抗\(R\)が小さくなってしまうと，実質的にCがほとんど見えなくなってしまい，Lだけが直接接地されているような状況になってしまうので，共振どころではないというイメージはすぐに湧くだろう．

　むしろ抵抗\(R\)が小さい状況においては真ん中の直列共振形が重宝する．つまり，\(R\)が小さい極限においては直列共振形をLCのみの共振回路そのものとみることができ，高い\(Q\)値を持つ共振系となる．今度は\(R\)が大きいときに直列共振形が不適となる．ここで，並列共振形と直列共振形のハイブリッドともいうべき共振回路が，図5の右側に示したLCC型である．これは\(R\)が十分大きいときにも小さいときにも共に共振回路として成立する．このように，共振形インバータの負荷に何がつながるのかにより，共振回路自身を最適に選ぶ必要がある．もちろん負荷側を工夫することもある．いずれにせよ共振回路と負荷は，互いに切っても切れない関係にあるのだ．

 

　本記事では，共振形インバータの簡単な紹介と，そもそも共振とは何かという議論をしてきた．次の記事では，なぜ共振形インバータが使われるのか，その活躍の理由と適用例などについて，簡潔に紹介していく．

　

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス