サイリスタによるコンバータの制御

 

　本記事ではサイリスタを用いたコンバータの出力電圧制御について考察する．その準備として，まずはサイリスタについて簡単におさらいしておこう．サイリスタは「導通のタイミングを遅らせることができるダイオード」である． サイリスタには導通の指令（トリガ電流）を入力するゲート（G）端子がある．図1でダイオードとサイリスタの回路素子を比較してみよう．

 

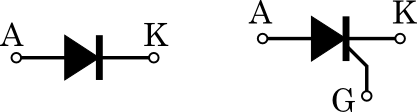
図1.ダイオード（左側）とサイリスタ（右側）

 

確かにサイリスタの回路記号はダイオードの回路記号にG端子を加えた形になっている．ダイオードは順バイアスをかければ（A端子をK端子よりも高電位にすれば）導通したが，サイリスタは順バイアスをかけただけでは導通しない．順バイアスをかけながらG端子にトリガ電流を入力したとき，はじめてサイリスタは導通するのだ．具体的にサイリスタがどのような動作をするのか，図2を例に見てみよう．

 

図2.サイリスタを用いたコンバータ（単相半波整流回路）

 

これは前記事の図1のダイオードをサイリスタに置き換えた回路である．前記事の図1の場合，\(V_{AC}\left({t}\right)>0\)の期間では必ず抵抗負荷に入力電圧\(V_{AC}\left({t}\right)\)がそのまま与えられていた．一方，本記事の図2では，\(V_{AC}\left({t}\right)>0\)になっても\(\Delta{T}[\rm{s}]\)の間だけ抵抗負荷には電圧が与えられていない．ダイオードは順バイアスになれば必ず導通するのだが，サイリスタは順バイアスになってもトリガ電流が入力されるまで導通しないのである．もう少し詳しく，図2のサイリスタTh1に入力するトリガ電流と\(V_{rect}\left({t}\right)\)との関係を図3に示そう．

 

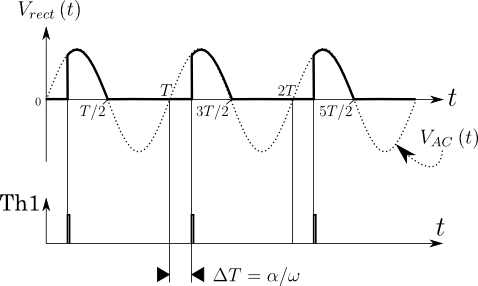
図3.図2のサイリスタTh1に入力するトリガ電流と\(V_{rect}\left({t}\right)\)との関係

 

このようにTh1のゲート端子にトリガ電流が入力されることで初めてサイリスタTh1が導通する．このトリガ電流のタイミングを変えることで\(\Delta{T}\)を調節できることがわかるだろう．\(\Delta{T}\)を電気角で表した\(\alpha\)を制御遅れ角と呼ぶ．実際に制御遅れ角\(\alpha\)を\({0}{[\rm{rad}]}\)から\(\pi[\rm{rad}]\)まで動かしたときの\(V_{rect}\left({t}\right)\)の推移をアニメーションにしてみよう．図4をご覧いただきたい．

 

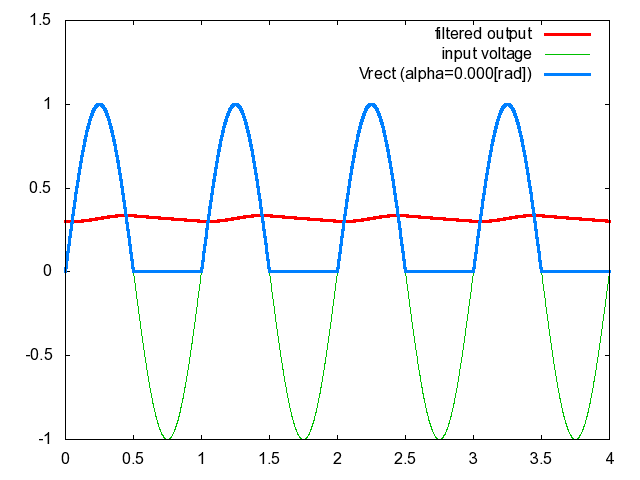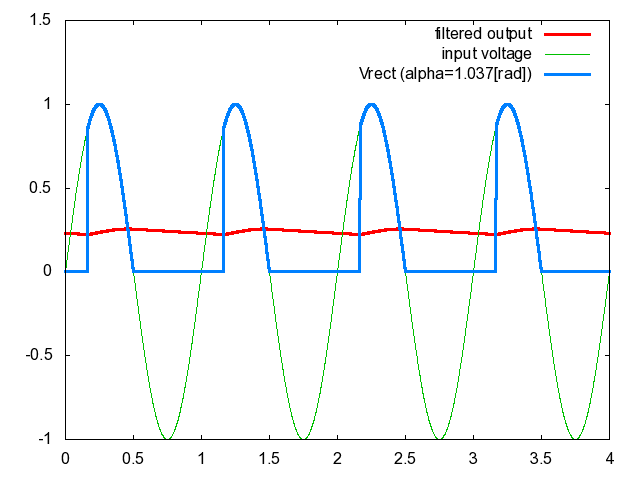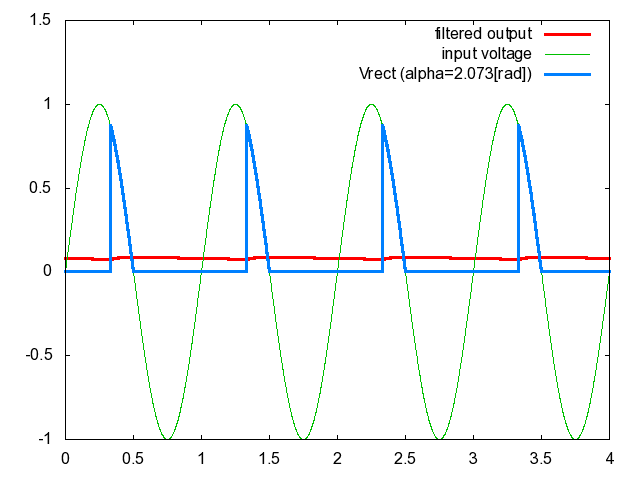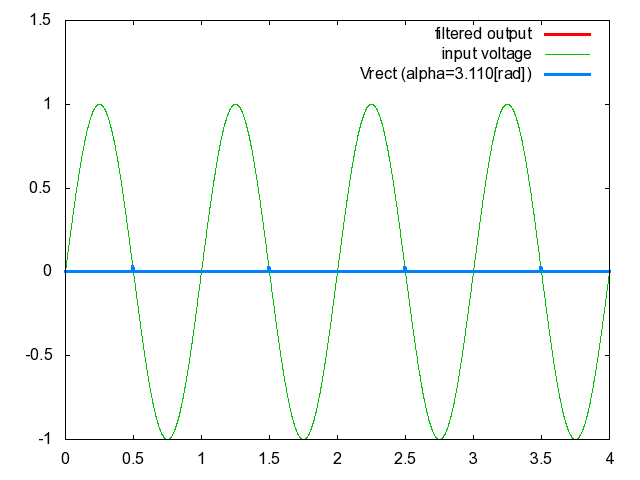
図4.図2における制御遅れ角\(\alpha\)と\(V_{rect}\left({t}\right)\)の関係

 

図4において，水色の波形は\(V_{rect}\left({t}\right)\)，赤色の波形は\(V_{rect}\left({t}\right)\)をフィルタにより平滑化した出力電圧である．ここで用いたフィルタは前記事の図3に示したフィルタ（LCフィルタ）であり，\(\overline{L}=\frac{\omega{L}}{R}=0.157\)，\(\overline{C}=\omega{C}R=0.0314\)とした．ただし\(R\)は抵抗負荷の抵抗値\([\rm{\Omega}]\)，\(\omega\)は単相交流の角速度\([\rm{rad/s}]\)である．実際の\(L\)と\(C\)の値はもっと大きいことに注意しよう．完全に平滑化された出力電圧はほとんど水平な直線となり面白くないのでここでは\(L\)と\(C\)をあえて小さ目の値に設定したのだ．

　次に，単相全波整流回路の出力電圧をサイリスタで制御してみよう．まずはダイオードによる単相全波整流回路を図5に示す．

 

図5.ダイオードによる単相全波整流回路

 

前記事でも考察したように，図5左側の回路の出力電圧\(V_{rect}\left({t}\right)\)は同図右側に示す通りとなる．ここで図6に示すように，図5のダイオードをサイリスタに置き換えると出力電圧\(V_{rect}\left({t}\right)\)はどのように変化するだろうか？

 

図6.図5のダイオードをサイリスタに置き換え

 

図6の置き換えにより，出力電圧\(V_{rect}\left({t}\right)\)は例えば図7のように変化する．

 

図7.図6の置き換えによる\(V_{rect}\left({t}\right)\)の変化

 

サイリスタは順バイアスになったとしてもゲートにゲート電圧を入力しない限り導通しない．図7右側は，順バイアスになってから\(\Delta{T}[\rm{s}]\)だけ待ってサイリスタにトリガ電流を入力した場合の出力電圧である．なぜこのような波形になるのか，また4つのサイリスタにどのようなタイミングでトリガ電流を加えればいいのか，これらの詳細については本書3.2の【例題10】をご参照いただきたい．

　最後に制御遅れ角\(\alpha\)を\({0}{[\rm{rad}]}\)から\(\frac{\pi}{2}[\rm{rad}]\)まで動かしたとき図7右側がどのように変化するのかアニメーションにしてみてみよう．図8に示す通り，今回も出力電圧の平滑化のためにLCフィルタを用いる場合を考える．

 

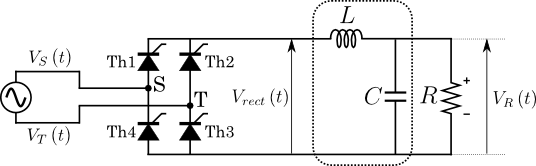
図8.図6右側にLCフィルタを加えた回路

 

図8の電圧（\(V_{rect}\left({t}\right)\)，\(V_{R}\left({t}\right)\)）が制御遅れ角\(\alpha\)の増加とともにどのように変化するのか，アニメーションにして図9に示そう．

図9.図8における制御遅れ角\(\alpha\)と出力電圧（\(V_{rect}\left({t}\right)\)，\(V_{R}\left({t}\right)\)）の関係

 

図9において，水色の波形は\(V_{rect}\left({t}\right)\)，赤色の波形はフィルタにより平滑化された出力電圧\(V_{R}\left({t}\right)\)である．ここでも図4と同様，\(\overline{L}=\frac{\omega{L}}{R}=0.157\)，\(\overline{C}=\omega{C}R=0.0314\)とした．ただし\(R\)は抵抗負荷の抵抗値\([\rm{\Omega}]\)，\(\omega\)は単相交流の角速度\([\rm{rad/s}]\)である．制御遅れ角\(\alpha\)を変化させることで，確かに平滑化された後の出力電圧\(V_{R}\left({t}\right)\)もコントロールできることが理解できただろう．

 

このように，サイリスタは交直電力変換技術の基幹を成す重要素子である．
サイリスタの実機についてはRSコンポーネンツのwebで閲覧・購入可能である．
実際のデバイスについて感触を得る好機会として参照をお勧めしておこう．

 

 

この項の内容に関する，オリジナル演習問題を絡めた詳細な解説は，

【入門演習 パワーエレクトロニクス】の第3章にて展開されています．是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス