コンバータの基本構造

 

　電力変換技術においてコンバータと言えば，交流電源から直流を作り出す回路のことである．コンバータは順変換回路，または整流回路とも呼ばれる．まず，最も単純なコンバータを図1に示そう．

 

図1.最も単純なコンバータ（単相半波整流回路）

 

このようにダイオード1つでコンバータを作れてしまうのだ．このとき出力電圧\(V_{rect}\left({t}\right)\)の波形（図1右側）は，入力交流電圧\(V_{AC}\left({t}\right)\)（同図左側）から負の電圧部分をカットした（\(0\)Vに置き換えた）ような形になる．コンバータは「正負両方の電圧を取りうる交流電源から正の電圧だけを作り出す回路」とも言い換えられるので，図1の回路は確かにコンバータである．ではなぜこうなるのか？ポイントはダイオードの性質にある．ダイオードは一方向にしか電流を流さない素子である．したがって図1では\(V_{AC}\left({t}\right)>0\)のときだけダイオードを介して抵抗に電流が流れ込み，\(V_{AC}\left({t}\right)<{0}\)のときにはダイオードが電流をブロックする．\(V_{AC}\left({t}\right)>0\)のときのダイオードの電圧降下を無視すれば，\(V_{rect}\left({t}\right)\)は\(V_{AC}\left({t}\right)\)と等しくなる．一方\(V_{AC}\left({t}\right)\leq{0}\)のときはダイオードが電流を流さないので\(V_{rect}\left({t}\right)=0\)となる．以上により，出力電圧\(V_{rect}\left({t}\right)\)の波形は，入力交流電圧\(V_{AC}\left({t}\right)\)から負の電圧部分をカットした波形になることがわかるだろう．

　図1のコンバータでは\(V_{AC}\left({t}\right)\leq{0}\)のとき抵抗負荷に電流は供給されない．このようなコンバータを半波整流回路と呼ぶ．これに対して，\(V_{AC}\left({t}\right)\leq{0}\)のときにも\(V_{AC}\left({t}\right)>{0}\)のときと同じ向きの電流を抵抗負荷に供給できるようにしたコンバータを全波整流回路と呼ぶ．図2をご覧いただきたい．

 

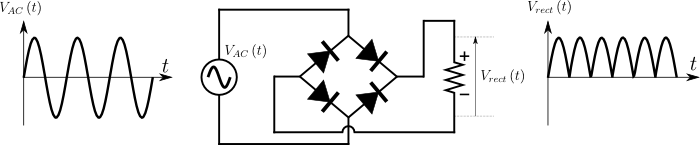
図2.ダイオードブリッジを用いたコンバータ（単相全波整流回路）

 

4つのダイオードを図2のように組み合わせることで，交流電圧\(V_{AC}\left({t}\right)<0\)のときにも抵抗負荷には正の電圧を与えることができる．図2のようにダイア形に接続された4つのダイオード部分をダイオードブリッジと呼ぶ．ダイオードブリッジは\(V_{AC}\left({t}\right)\)の正負に応じて交流電源と抵抗負荷の接続の順手・逆手を入れ替える役目を果たす．これにより，\(V_{AC}\left({t}\right)\)の正負によらず，抵抗負荷には常に上から下に電流が流れるのだ．図1のコンバータでは\(V_{AC}\left({t}\right)<0\)のときには交流電源からの電流をブロックしていたのに対し，図2のコンバータでは\(V_{AC}\left({t}\right)<0\)のときにも交流電源から抵抗負荷に電流を供給し続けているのである．

　ここで図1と図2の出力電圧\(V_{rect}\left({t}\right)\)を見ると，激しく時間変動していることがわかる．これは大抵の場合で問題となる．例えばパソコンのような電子回路の直流電源として図2の電圧\(V_{rect}\left({t}\right)\)を用いると，動作しないことは当然のこと，機器自体の損傷も考えられる．したがって図1や図2などのコンバータには，多くの場合で出力電圧の時間変動を抑えるためのフィルタが必要なのである．図2の単相全波整流回路に出力フィルタを付けた例を図3に示す．

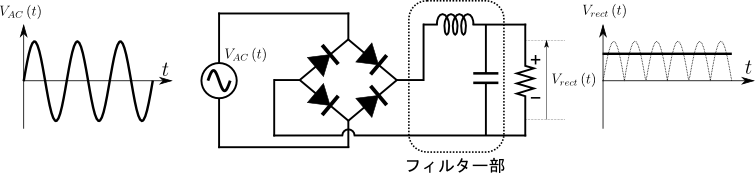
図3.出力フィルタ付きのコンバータ（単相全波整流回路の場合）

 

この例ではLCフィルタ（インダクタLとキャパシタCを組み合わせたフィルタ）を用いている．出力にフィルタを挿入することで，抵抗負荷に加わる電圧は平滑化される（時間的にほぼ一定となる）．出力を平滑化するためにコンバータの出力側に挿入されるフィルタのことを平滑回路とも呼ぶ．もちろん用途に応じてLやCのみによる平滑回路も考えられる．それぞれの出力電圧や入力電流などの特徴については【入門演習 パワーエレクトロニクス】の3.2，【例題7】および【例題8】を参照いただきたい．

　さて，ここからは三相交流のコンバータについて考察していこう．その準備として，まず図2で登場したダイオードブリッジを書き換える．図4をご覧いただきたい．

 

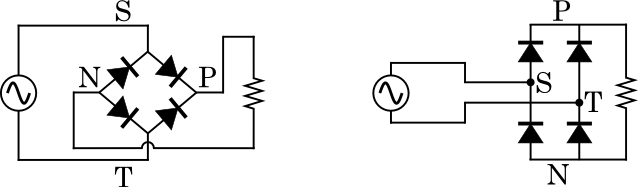
図4.ダイオードブリッジの書き換え

 

図4の左側と右側は完全に同じ回路である．同図右側のように書き換えることで，単相から三相になったときにコンバータがどのような形に変化すればよいか予想しやすくなるのだ．実際に三相交流のコンバータを図5に示そう．

 

図5.三相交流のコンバータ（三相全波整流回路）

 

図4右側（単相交流のコンバータ）は2対（計4つ）のダイオードを持っているのに対し，図5（三相交流のコンバータ）は3対（計6つ）のダイオードを持っていることがわかる．交流の各相に1対のダイオードが対応しているのである．図5の出力側の端子電圧\(V_{P}\)，\(V_{N}\)の波形がどのようになるのか，図6に示そう．

 

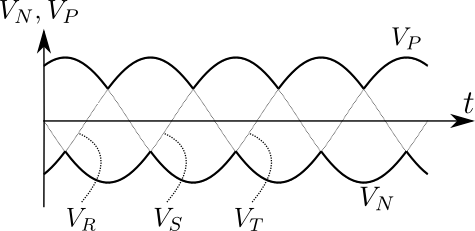
図6.図5の出力側の端子電圧\(V_{P}\)，\(V_{N}\)

 

\(V_{P}\)は三相交流の各相\(V_{R}\)，\(V_{S}\)，\(V_{T}\)のうち最高の電圧と等しくなり，\(V_{N}\)は\(V_{R}\)，\(V_{S}\)，\(V_{T}\)のうち最低の電圧と等しくなるのだ．詳細は本書3.2の【例題4】および【例題5】をご覧いただきたい．

　ここまでで，単相交流から三相交流まで，コンバータの基本構造について一通りカバーできた．ここからは，サイリスタを用いた出力電圧調整について簡単に触れておきたい．サイリスタを用いた三相全波整流回路を図7に示す．

 

図7.サイリスタを用いた三相全波整流回路

 

図7は，図6のダイオードをサイリスタに置き換えたものである．サイリスタの動作については次の記事で説明するとして，ここでは図7の出力側の端子電圧\(V_{P}\)，\(V_{N}\)がどのような波形になるのか示すに止めよう．図8をご覧いただきたい．

 

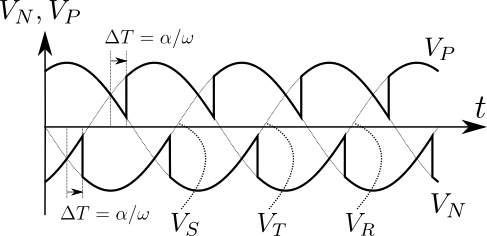
図8.図7の出力側の端子電圧\(V_{P}\)，\(V_{N}\)

 

図6と比べると，図8では相の切り替えのタイミングが\(\Delta{t}\)だけずれていることがわかる．この\(\Delta{t}\)の期間では，\(V_{P}\)が三相交流の各相\(V_{R}\)，\(V_{S}\)，\(V_{T}\)のうちの最高電圧と等しくないか，もしくは\(V_{N}\)が\(V_{R}\)，\(V_{S}\)，\(V_{T}\)のうちの最低電圧と等しくない．すなわち\(\Delta{t}\)の間，出力電圧\(V_{P}-V_{N}\)はダイオードを用いた場合（図6）の\(V_{P}-V_{N}\)よりも低くなる．この\(\Delta{t}\)を大きくすれば，出力電圧\(V_{P}-V_{N}\)の平均値はさらに低下することがわかるだろう．\(\Delta{t}\)を調節すれば\(V_{P}-V_{N}\)の平均値をコントロールできるのである．ここで，コンバータの出力側に図3に示すような平滑回路を設ければ，得られる直流電圧は出力電圧\(V_{P}-V_{N}\)の平均値と等しくなるので，\(\Delta{t}\)を調節することで平滑化された後の直流電圧をコントロールできるとも言える．

 

　次の記事では，なぜサイリスタを用いることでコンバータ出力を制御できるのか，サイリスタの動作も含めて考察していこう．

 

 

この項の内容に関する，オリジナル演習問題を絡めた詳細な解説は，

【入門演習 パワーエレクトロニクス】の第3章にて展開されています．是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス