チョッパ回路の制御

 

　本記事において，チョッパ回路の出力電圧や出力電流がどのように制御されるのか，その概要を説明していこう．チョッパ回路にはいろいろあるが，ここでは降圧チョッパ回路を題材とする．

 

 

図1.降圧チョッパ回路と通流率\(D\)

 

 

　前々回の記事でも説明したが，チョッパ回路の出力電圧（出力電流）をコントロールしたければ，半導体スイッチの開閉を制御する方形波のデューティ比\(D\)（以降"通流率"と呼ぶ）を変化させてやればよい．図1に示す降圧チョッパ回路の出力電圧\(V_{out}\)は

$$V_{out}=DV_{in} \tag{1}$$

というように，\(D\)に比例しており，\(D=1\)のとき最大となって入力電圧\(V_{in}\)と等しくなる．つまり，通流率\(D\)と出力電圧\(V_{out}\)の関係をグラフにすると，次の図2のようになる．

 

 

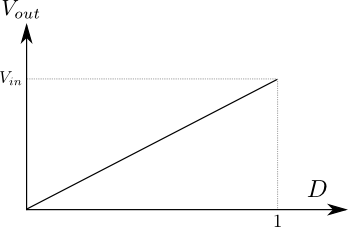
図2.降圧チョッパ回路の通流率\(D\)と出力電圧

 

 

　この関係を踏まえると，例えば\(V_{out}\)を階段状に変化させたいと思えば，降圧チョッパ回路の通流率も階段状に変化させればよい．つまり，スイッチング制御信号のパルス幅を下記の図3に示すように変化させてあげればよいことがわかるだろう．

 

 

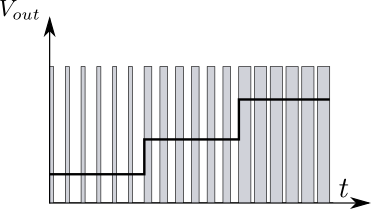
図3.PWM制御のイメージ

 

 

　これはスイッチング制御信号のパルス幅を調整していることに他ならないので，PWM制御そのものである．つまり，チョッパ回路の出力制御も結局はPWM制御を用いているのである．ただし，実際のチョッパ回路にはインダクタやキャパシタが用いられているので，通流率を変えたからといって即座にそれが出力電圧に反映される訳ではなく，ある時定数を持った過渡応答を示すことを忘れてはならない．

 

 

図4.実際の降圧チョッパ回路における過渡応答

 

 

　実際はこの図4に示すような一定の時定数を経て，ある出力電圧に落ち着く．チョッパ回路の制御システムを組むときには，この時定数やダンピングファクターを無視した設計はできない．これらの過渡応答を考慮に入れないと，制御系がある周波数帯と共振してしまったり，最悪の場合不安定状態（つまり発振状態）に陥ってしまうのだ．

　このことを踏まえて，実際の制御システムがどのように組まれるのか，その例を示したものが次の図5である．

 

図5.降圧チョッパ回路の出力電圧制御

 

 

　この図5は，出力電圧\(V_{out}\)がリファレンス電圧\(V_{ref}\)と等しくなるように動作する制御システムを表している．まず，\(V_{out}\)がリファレンス電圧\(V_{ref}\)に対してどれくらい高いのか（低いのか）を検出し，その検出結果（偏差と呼ぶ）をある応答特性\(G\left({s}\right)\)を持った補償器に入力し，その補償器の出力をスイッチの通流率\(D\)に変換するというシステムである．この補償器の伝達関数\(G\left({s}\right)\)を工夫することにより，出力電圧\(V_{out}\)を迅速に制御しつつ制御系全体の安定性も確保することが可能である．この辺りの数学的な議論は書籍などで展開することとする．

　図5においては出力電圧\(V_{out}\)を制御したが，もちろん出力電流を制御するシステムも考えることができる．次の図6は降圧チョッパ回路の出力電流\(I_{L}\)を調整するフィードバック制御系を表している．

 

図6.降圧チョッパ回路の出力電流制御

 

 

　図5の出力電圧制御のときと同様，図6の出力電流制御のときにも出力電圧\(I_{L}\)とリファレンス電圧\(I_{ref}\)の差\(I_{L}-I_{ref}\)をスイッチの通流率\(D\)へフィードバックするという制御系が組まれている．そしてこのフィードバック制御の安定性を確保するため，フィードバック経路に補償器\(G\left({s}\right)\)が挿入されている点も図5と同様である．ただし，今回は出力電圧\(V_{out}\)ではなく出力電流\(I_{L}\)を直接計測しているので，出力容量に起因する遅延が避けられている分だけ補償器の伝達関数\(G\left({s}\right)\)が異なるものになっていることを補足しておこう．

　次の図7では，出力電圧制御でも出力電流制御でもなく，負荷（この場合はモータ）の状態に応じたより最適な制御も当然考え得ることを示している．

 

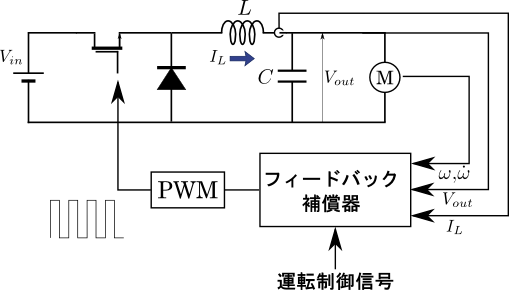
図7.降圧チョッパ回路のベクトル制御

 

 

　これは負荷がモータなので，事実上ベクトル制御を表す図であるともいえる（その場合はモータは誘導機や同期機であり，PWM制御により交流が出力される場合だが）．このように，一定電圧（図5）や一定電流（図6）の制御だけでなく，負荷の状態をリアルタイムで精密に計測しながら臨機応変に最適な状態を達成する制御こそ，昨今の半導体制御の有用性を指し示す何よりの好例と言えるだろう．

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス