チョッパ回路のリップル電圧

 

　ここまでは，チョッパ回路の出力電圧がほぼ一定であるという前提をもとに議論してきた．しかしチョッパ回路の動作は，半導体スイッチをひっきりなしにON-OFFさせるというものなので，「出力もそれに合わせて大きく揺れてしまうのではないか？」という疑問は当然出てくるだろう．そこでここでは，チョッパ回路の出力電圧がどれだけ揺れるのか，その脈動の大きさ（リップル電圧）を実際に計算してみることにしよう．

 

図1.降圧チョッパ回路と各パラメータ

 

 

　今回は図1に示す降圧チョッパ回路を題材に計算を進める．もちろんここで行う計算は，他のタイプについても応用可能である．早速解析に入ろう．

　まず，前回の記事においても説明されているように，\(V_{X}\)は\(V_{in}\)と\(0V\)とを往復する矩形波となっており，その\(V_{X}\)の平均電圧が\(V_{out}\)の平均電圧と等しくなる．このことを用いると，インダクタを流れる電流\(I_{L}\)の揺れの大きさが見積もれる．これはリップル電圧を求めるときに役立つはずである．そこで，次の図2に\(V_{X}\)と\(I_{L}\)の波形を描いてみる．

 

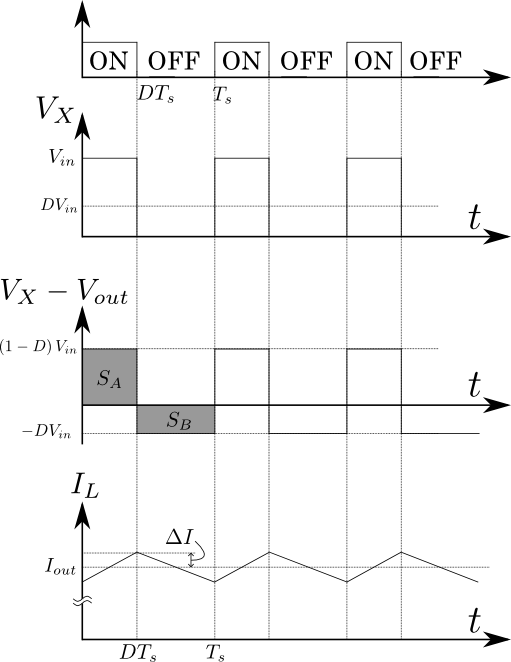
図2.降圧チョッパ回路（図1）の\(V_{X}\)，\(I_{L}\)

 

 

　\(I_{L}\)が図2に示したような三角波になるのは直感的にも理解できる．MOSFETがONしているときはインダクタの左側が高電圧になるので\(I_{L}\)は増加し，逆にMOSFETがOFFしているときはインダクタの右側が高電圧になるので\(I_{L}\)は減少する．これを式で表すと，次の式(1)のようになる．

$$L\frac{dI_{L}}{dt} = V_{X}-V_{out} \tag{1}$$

この式(1)の右辺は，MOSFETがONのときは正であり，OFFのときは負になっている．（図2の下から２番目のグラフ）

　式(1)を用いれば簡単に図2の\(\Delta{I}\)も求められそうだ．しかし注意深い人はここで「待てよ？」となる．\(V_{X}\)は矩形波であるとわかったが，\(V_{out}\)の波形はこれから求めるのではないか？それなのにすでに図2において\(V_{out}\)を一定として扱ってしまっている．\(V_{out}\)を一定電圧として\(V_{out}\)のリップル電圧（一定でない成分）を求めようと言うのである．これはいいのだろうか？

　結論から言えば，これはOKである．\(V_{out}\)の平均電圧と比べてこのリップル電圧が十分小さければ，\(V_{out}\)を一定電圧として\(V_{out}\)のリップル電圧を求めてよい．例えば\(V_{out}\)の平均電圧に対してそのリップル電圧が\(1\%\)程度ならば，\(V_{out}\)を一定電圧として求めた\(V_{out}\)のリップル電圧の計算誤差も\(1\%\)のオーダーである．ということで，\(V_{out}\)を一定電圧として計算を進めていく．

　\(V_{out}\)は\(V_{X}\)の平均電圧であり，

$$V_{out}=DV_{in} \tag{2}$$

これを式(1)に代入して，

$$L\frac{dI_{L}}{dt} = V_{X}-DV_{in} \tag{3}$$

ここで\(\Delta{I}\)を求めるべく式(3)を\([0,DT_{s}]\)について積分すると

$$L\left(I_{L}\left({DT_{s}}\right)-I_{L}\left({0}\right)\right) = \int_{0}^{DT_{s}}\left(V_{X}-DV_{in}\right)dt = D\left(1-D\right)T_{s}V_{in} \tag{4}$$

図2の一番下のグラフと見比べれば，式(4)左辺のカッコ内は\(2\Delta{I}\)であることがすぐにわかる．すると

$$\Delta{I} = \frac{D\left(1-D\right)T_{s}V_{in}}{2L} \tag{5}$$

と求まる．ここまでくれば電圧リップルの計算は目前である．あとは出力電流と出力電圧との間で成り立つ関係が分かればよい．

ということで，次の図3において，インダクタを流れる電流\(I_{L}\)と出力電圧\(V_{out}\)がどのような波形になるか見てみよう．

 

図3.降圧チョッパ回路の電流\(I_{L}\)と出力電圧\(V_{out}\)の関係

 

 

　\(I_{L}\)は三角波なので，それに合わせて出力電圧\(V_{out}\)も上下する．この場合は出力に容量\(C\)が取り付けられているので，容量に流れ込む電流\(I_{L}-I_{out}\)の時間積分から出力電圧\(V_{out}\)を計算できる．具体的には，図3に示すような積分区間\([t_{a},t_{b}]\)について

$$V_{out}\left({t_{b}}\right)-V_{out}\left({t_{a}}\right)= \frac{1}{C}\int_{t_{a}}^{t_{b}}\left(I_{L}-I_{out}\right)dt \tag{6}$$

が成り立ち，かつこの式(6)の左辺は図3の\(\Delta{V}_{p-p}\)なので

$$\Delta{V}_{p-p}= \frac{1}{C}\int_{t_{a}}^{t_{b}}\left(I_{L}-I_{out}\right)dt \tag{7}$$

となる．この式(7)右辺の積分は図3真ん中の影で示した三角形の面積\(\Delta{Q}\)となっている．この三角形の高さは式(5)の\(\Delta{I}\)そのものであり，また底辺の長さは\(t_{b}-t_{a}\)，つまり\(\frac{T_{s}}{2}\)であるから，結局式(7)は

$$\Delta{V}_{p-p}= \frac{T_{s}\Delta{I}}{4C} \tag{8}$$

これに式(5)を代入して，

$$\Delta{V}_{p-p}= \frac{D\left(1-D\right)T_{s}^{2}}{8CL}V_{in} \tag{9}$$

 

これにて電圧リップルの大きさを求めることができた．この式(9)によれば，容量\(C\)やインダクタンス\(L\)が大きければそれに反比例して\(\Delta{V}_{p-p}\)が小さくなることがわかる．また，スイッチング周期が短ければその２乗に比例して\(\Delta{V}_{p-p}\)が小さくなることも理解できる．チョッパ回路の出力が揺れてしまうのは原理的に仕方のないことだが，その揺れの大きさはスイッチング周波数を高めることである程度低減可能である．ただし，スイッチング周波数を高めることは半導体素子に高速動作を要求し，またスイッチング損失も増加させるため限界がある．また容量\(C\)やインダクタンス\(L\)についても，大きくし過ぎると制御の応答特性を劣化させるし，コスト的な制約もあるため，式(9)を際限なく小さくできると考えるのは誤りである．　

　結局のところ，「チョッパ回路の出力電圧が一定とみなせるくらいにリップルを常に抑制できる」と言い切ることはできない．アプリケーションによっては大変な低ノイズを要求する場合もあるからだ．しかしMOSFETやIGBTなどの高速スイッチングを得意とする素子を用いれば，例えばリップル電圧を出力電圧の\(1\%\)以下にすることは容易く，その程度のリップルであれば電子回路から動力系まで，大半のアプリケーションで許容できる．

 

その他のチョッパ回路のリップル電圧についても，上記と同様の計算を繰り返すことにより算出可能である．

 

 

 

この項の内容に関する，オリジナル演習問題を絡めた詳細な解説は，

【入門演習 パワーエレクトロニクス】の4.2にて展開されています．是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス