チョッパ回路の通流率と出力電圧
今回の記事では,チョッパ回路における,通流率(半導体スイッチング素子がONしている時間の割合,デューティー比とも呼ぶ)と出力電圧との関係を明らかにしていこう.以下の図1に示す降圧チョッパ回路と昇圧チョッパ回路について具体的に計算を行っていく.

図1.降圧チョッパ回路(左)と昇圧チョッパ回路(右)
まずは降圧チョッパ回路について,通流率と出力電圧の関係を導出しよう.
降圧チョッパ回路(buck Converter)の場合
ここでのゴールは,次の図2に示した降圧チョッパ回路について,出力電圧\(V_{out}\)を求めることである.

図2.降圧チョッパ回路と回路パラメータ
出力電圧\(V_{out}\)を知りたければ,図2における\(V_{X}\)の時間平均を求めればよい.\(V_{X}\)の時間平均が\(V_{out}\)そのものとなるのである.これはインダクタの性質からすぐに導かれる.実際にここで導いてみよう.
まずインダクタに流れる電流を\(I_{L}\)とすると,インダクタにかかる電圧は\(V_{X}-V_{out}\)であるから,
これをスイッチング1周期分\(T_{s}\)について積分してやると,
つまり,
式(2)の左辺は\(0\)である.なぜなら,定常状態であればスイッチング毎に同じ電流・電圧を繰り返すはずであり,\(I_{L}\left({\tau+T_{s}}\right) = I_{L}\left({\tau}\right)\)が成立するからである.よって式(2)は次のように書き換えられる.
これは,\(V_{X}\)の1周期平均と\(V_{out}\)の1周期平均が等しいことを表している.\(V_{out}\)が一定である(リップル電圧が十分小さい)と仮定すると,式(3)を用いて\(V_{out}\)は
と表される.
同様にして,この「定常状態においてはインダクタ両端の1周期平均電圧が等しい」という関係を用いれば,あらゆるチョッパ回路の出力電圧\(V_{out}\)を簡単に求めることができる.今回の降圧チョッパ回路については,この式(4)を用いればよい.つまり,\(V_{X}\)の波形が分かれば,あとは式(4)を使って\(V_{out}\)が求められるのだ. ということで早速\(V_{X}\)の波形を次の図3に示そう.
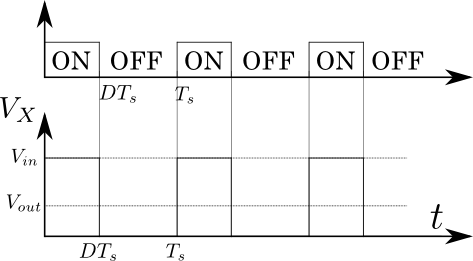
図3.降圧チョッパ回路の\(V_{X}\)と\(V_{out}\)
図3では,スイッチング1回当たりMOSFETがONする期間を\(DT_{s}\)とする.つまり,通流率を\(D\)とする.この図3に示すように\(V_{X}\)はMOSFETがONしているときは\(V_{in}\)となり,OFFしているときは\(0V\)となる.ここで,ダイオードにおける電圧降下(通常\(1V\)程度)は無視した.この場合,電圧\(V_{X}\)の平均値は\(DV_{in}\)となることがすぐに計算できるだろう.よって,式(4)から\(V_{out}\)は
となる.これから昇圧比\(M\left({D}\right)\)は
と導かれる.降圧チョッパ回路においては,通流率\(D\)が出力電圧\(V_{out}\)と比例しているということが理解できただろう.
昇圧チョッパ回路(boost Converter)の場合
上記で示した降圧チョッパのときの計算と同様,昇圧チョッパ回路についても\(V_{out}\)を求めていこう.今回計算する昇圧チョッパの回路図を次の図4に示す.
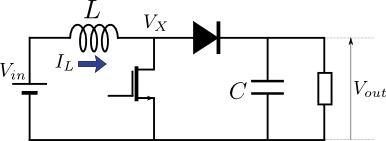
図4.昇圧チョッパ回路と回路パラメータ
ここでも,「定常状態においてはインダクタ両端の1周期平均電圧が等しい」という性質を用いる.すると,今回の図4では\(V_{in}\)の時間平均(つまり\(V_{in}\)そのもの)が\(V_{X}\)の1周期分時間平均と等しいことになるので,
が成立する.\(V_{X}\)の平均値が分かればこの式(7)を用いて\(V_{out}\)が求まるので,早速\(V_{X}\)の波形を次の図5に示してみる.
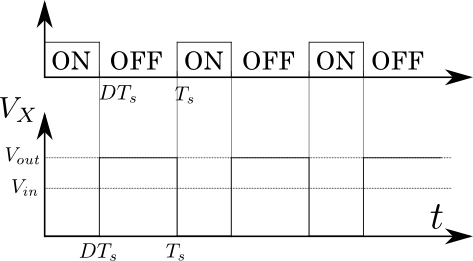
図5.昇圧チョッパ回路の\(V_{X}\)
昇圧チョッパにおいては,MOSFETがONのときは\(V_{X}\)は\(0V\)となり,OFFのときはダイオードを介して出力とつながるので\(V_{out}\)となる.\(V_{X}\)は,全体からの割合にして\(D\)の時間だけ\(0V\)であり,\(\left({1-D}\right)\)の時間だけ\(V_{out}\)となっているので,その平均電圧\(\overline{V}_{X}\)は,
と計算できる.これが式(7)の右辺になるので,
となる.これを\(V_{out}\)について解けば
これから昇圧比\(M\left({D}\right)\)は
と求められる.
次に,この昇圧比\(M\left({D}\right)\)をいろいろなチョッパ回路に適用した場合に通流率\(D\)に対してどのような関係になるのか,その結果だけ簡単に紹介しよう.
いろいろなチョッパ回路の昇圧比\(M\left({D}\right)\)
次の図6は,前の記事「いろいろなチョッパ回路」において紹介されている5つのタイプのチョッパ回路について昇圧比\(M\left({D}\right)\)をプロットしたものである.
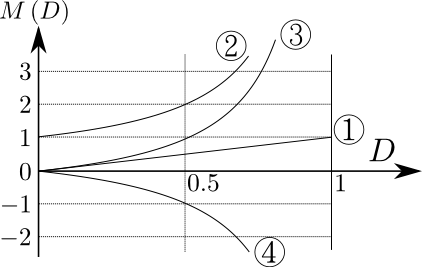
図6.いろいろなチョッパ回路の昇圧比
①は式(6)のプロットで降圧チョッパの昇圧比,②は式(11)のプロットで昇圧チョッパの昇圧比である.
また,昇降圧チョッパ回路の昇圧比は
となっており,③のようなプロットとなる.
そして非反転の昇降圧チョッパ回路,およびSEPIC回路の昇圧比はともに
となり,プロットは④である.
これらもまったく同じように「定常状態においてはインダクタ両端の1周期平均電圧が等しい」というインダクタの性質を用いることで簡単に導出できるので,上記の計算をヒントに是非一度トライしていただきたい.
次は,この出力電圧が実は少し揺れていることを定量的に議論しよう.
この項の内容に関する,オリジナル演習問題を絡めた詳細な解説は,
【入門演習 パワーエレクトロニクス】の4.2にて展開されています.是非ご参照を!!
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.



 同機機のベクトル図(入門編)
同機機のベクトル図(入門編)






