サイクロコンバータの基本構造

 

　本記事ではサイクロコンバータの基本構造について解説する．まずサイクロコンバータとは何か？一言で言えば，「サイリスタを用いて交流電源から新たな周波数の交流を作り出す回路」となる．例えば，サイリスタコンバータを用いると，\(60[\rm{Hz}]\)の交流電源から\(10[\rm{Hz}]\)の交流を生成できる．一般に，交流電源の周波数（ここでは\(60[\rm{Hz}]\)）よりも十分低周波（\(1/3\)以下の周波数）の交流を出力することができる．ではなぜサイクロコンバータは交流から新たな周波数の交流を作り出せるのだろうか？サイクロコンバータの原理は一体どうなっているのだろうか？この疑問に答えるためには，まず三相コンバータの動作原理を理解しておく必要がある．図1にサイリスタを用いた三相コンバータを示そう．

 

図1.サイリスタを用いた三相コンバータ（三相全波整流回路）

 

図1左側に三相コンバータの回路図，同図右側に整流後の電圧\(V_{X}\left({t}\right)\)の波形を示している．同図右側の点線と実線はそれぞれ，異なる2つの制御遅れ角（サイリスタを導通させるタイミング）に対する\(V_{X}\left({t}\right)\)の波形である．前記事”サイリスタによるコンバータの制御”でも説明した通り，制御遅れ角を変えることで\(V_{X}\left({t}\right)\)の平均値が変化し，結果として直流出力電圧\(V_{out}\left({t}\right)\)を調整することができるのである．実際に制御遅れ角\(\alpha\)を変化させたときに図1の\(V_{X}\left({t}\right)\)と\(V_{out}\left({t}\right)\)がどのように変化するのか，アニメーションにして見てみよう．図2をご覧いただきたい．

 

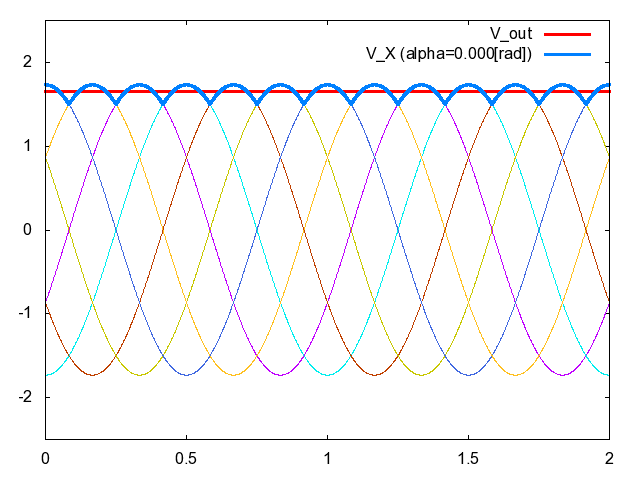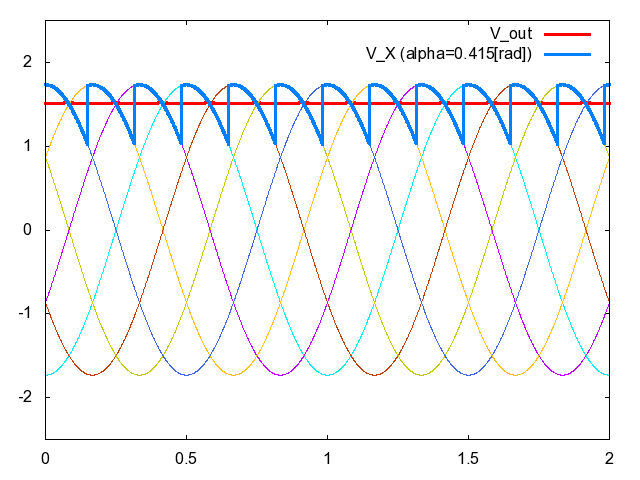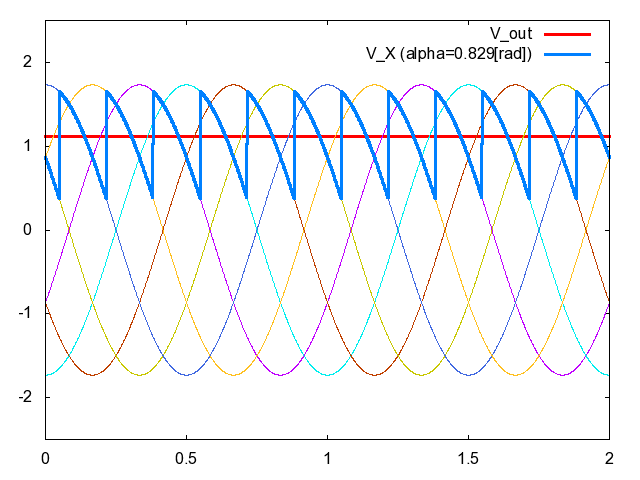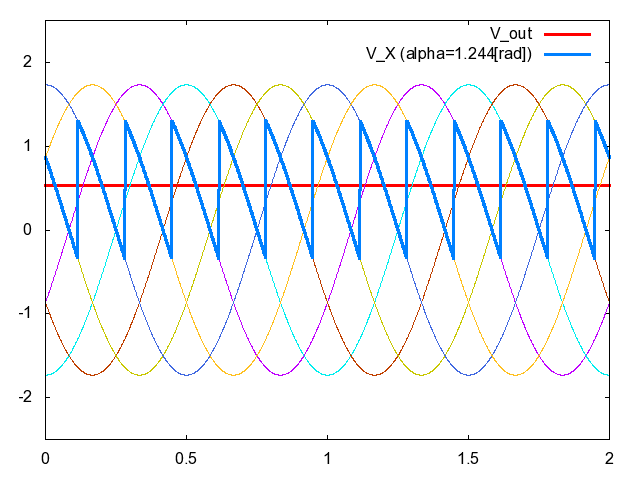
図2.図1の三相コンバータの電圧波形（青色太線：\(V_{X}\left({t}\right)\)，赤色太線：\(V_{out}\left({t}\right)\)）と制御遅れ角\(\alpha\)

 

整流後の電圧\(V_{X}\left({t}\right)\)を青色太線で，フィルタ後の電圧\(V_{X}\left({t}\right)\)を赤色太線でそれぞれ示した．ここで用いたフィルタは前記事のアニメーションで用いたものと同じLCフィルタであり，\(\overline{L}=\frac{\omega{L}}{R}=0.157\)，\(\overline{C}=\omega{C}R=0.0314\)である．ただし\(R\)は抵抗負荷の抵抗値\([\rm{\Omega}]\)，\(\omega\)は単相交流の角速度\([\rm{rad/s}]\)を表す．図2を眺めているうち，「制御遅れ角\(\alpha\)を動かせば出力電圧\(V_{out}\left({t}\right)\)を交流にすることもできるのではないか？」という期待が湧くだろう．実際図1の制御遅れ角\(\alpha\)を動的に調整することで，図3に示すような出力電圧\(V_{out}\left({t}\right)\)のような波形を生成できる．

 

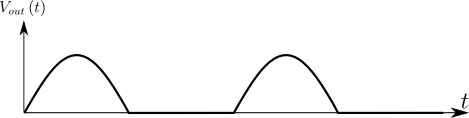
図3.図1の制御遅れ角\(\alpha\)を動的に調整することで得られる出力電圧\(V_{out}\left({t}\right)\)の波形

 

図3に示す電圧波形は正弦波の上半分のみとなっている．実は，図1に示した三相コンバータだけでは負の電圧を出力することができないのだ（正確には負の電流を出力できない）．これは何故なのだろうか？サイリスタはダイオードと同様，一方向の電流しか流さない．図1のサイリスタの向きを見れば，\(I_{out}\left({t}\right)<{0}\)は許されないことがわかる．図1では\(I_{out}\left({t}\right)\geq{0}\)でなければならないのだ．「制御遅れ角\(\alpha\)を動かすことで出力電圧\(V_{out}\left({t}\right)\)を動的に調整できる」という話は，\(I_{out}\left({t}\right)\geq{0}\)という範囲内においてのみ正しいのである．例えば図1の負荷が抵抗負荷ならば，\(V_{out}\left({t}\right)\)が負にならない範囲でのみ\(V_{out}\left({t}\right)\)を調整できると言い換えられる．図3の出力電圧\(V_{out}\left({t}\right)\)の波形が\({0}[\rm{V}]\)以上になっているのはこのためである（図3では図1の負荷は抵抗負荷であるとしている）．しかし交流を生成するためには当然ながら負の電流も出力できなければならない．そこで図1の三相コンバータを図4のように改造してみよう．

 

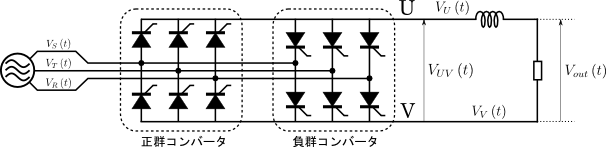
図4.単相出力のサイクロコンバータ1（6パルスサイクロコンバータ）

 

図4の正群コンバータは図1のサイリスタ部そのものであり，同図の負群コンバータは図1のサイリスタ部の極性を反転させたものである．図1のコンバータは\({0}[\rm{A}]\)以上の電流しか出力できないので，正群コンバータは\({0}[\rm{A}]\)以上の電流しか出力できず，一方負群コンバータは\({0}[\rm{A}]\)以下の電流しか出力できない．これら2つを並列にすることで，正の電流だけでなく負の電流も出力できるようになるのだ．これがサイクロコンバータの基本的な仕組みである．

　さて，図4では12個のサイリスタを用いていたが，6個のサイリスタでサイクロコンバータを構成することも可能である．図5をご覧いただきたい．

 

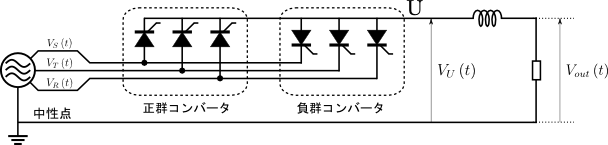
図5.単相出力のサイクロコンバータ2（3パルスサイクロコンバータ）

 

図4と図5を見比べると，図4では使われていた下半分のサイリスタ6個が図5ではまるまる消えていることがわかる．図4では電圧\(V_{U}\left({t}\right)\)の生成用に6個，電圧\(V_{V}\left({t}\right)\)の生成用に6個，計12個のサイリスタが使われている．一方図5では単相出力の一端が接地されているので，接地された端子側のサイリスタ6個が不要となり，削除されたのだ．図5では接地していない端子側のサイリスタ6個のみ残しておけばよいのである．ただし，サイリスタの数を減らした分だけ，図5の出力波形は図4のものに比べてより理想的な正弦波からかけ離れたものとなっていることに注意しよう．この辺りの詳しい議論については，【入門演習 パワーエレクトロニクス】のp.245を参照いただきたい．

　本記事の最後に，単相出力のサイクロコンバータを3つ組み合わせることで三相出力のサイクロコンバータを構成できることを示そう．

図6をご覧いただきたい．

 

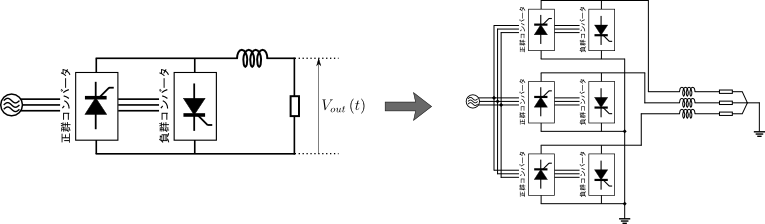
図6.単相出力のサイクロコンバータ（左）と三相出力のサイクロコンバータ（右）

 

図6左側は単相出力のサイクロコンバータである．この具体的な回路構成としては，図4と図5のどちらを想像してもらっても構わない．同図右側に示す通り，同図左側に示す単相出力のサイクロコンバータを3つ組み合わせることで，三相出力のサイクロコンバータを構成することができる．ここで示していることは，単に「三相交流の各相に単相出力のサイクロコンバータをそれぞれ1つずつ割り当てている」というだけのことである．三相交流を出力するためには3つの正弦波電圧を用意できればよいのだから，単相出力のサイクロコンバータが3つあれば事足りることは容易に想像がつくことだろう．

　サイクロコンバータの基本構造についての解説は以上である．次の記事ではサイクロコンバータの動作について詳しく検討しよう．

 

 

この項の内容に関する，オリジナル演習問題を絡めた詳細な解説は，

【入門演習 パワーエレクトロニクス】の第3章にて展開されています．是非ご参照を!!

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス