変圧器のPU法(入門編)
ここからはPU(Per Unit)法について説明していきたい.またの名を単位法などとも呼ぶが,これは電力工学の解析全般において絶大なる威力を発揮する非常に優れた表記法であり,特に変圧器が存在する系にPU法を適用した途端,変圧器が姿を消してしまい(多くの場合単なるインダクタに置き換わる),とにかく回路が簡単になる.その単純化の見事さには誰もが驚くのではないだろうか.
これから変圧器にPU法を適用していくわけだが,まずはPU法とは何かについての簡単な説明から入ろう.
PU法とは何か
PU法というのは,電流・電圧・インピーダンスなどをはじめ,あらゆる電気量に適用できる表記法の1つであり,ある基準値(一般的には定格値)からの倍数を示す表記法である.また,今回説明する変圧器以外にも,あらゆる電気機械をPU法で解析することが可能である.例えば同期機にPU法を適用したケースは”同期機のベクトル図へのPU法適用”に説明されている.
一番簡単な例として,家庭内のコンセントの電圧をPU法で表してみよう.あるときのコンセントの電圧が\(V_{o}=102[V]\)だとして,これをPU法で表したらどうなるだろうか?まずPU法を適用するためには基準となる電圧が必要である.これを基準電圧\(V_{base}\)と呼ぶことにするが,この基準電圧\(V_{base}\)としては,一般的に定格値が選ばれる.ここでは一般的な家庭のコンセント電圧として\(100V\)が選ばれるだろう.すると先ほどのコンセントの電圧\(V_{o}\)は基準電圧\(100V\)の\(1.02\)倍ということで,\(1.02 [p.u.]\)と表される.これがPU法である.つまり繰り返しになるが,PU法というのは基準値からの倍数を示す表記法のことを指すのである.
では上記を踏まえ,PU法の数学的な定義を与えよう.例として,電圧\(V\)・電流\(I\)・有効電力\(P\)をPU法で表してみる.これらの基準として,基準電圧\(V_{base}\)・基準電流\(I_{base}\)・有効電力\(P_{base}\)とすれば,
となる.基準値からの倍率を表しているだけなので,定義は至って簡単であろう.単位は一般的に\(p.u.\)と表記される.また,本記事では詳しくは触れないが%(パーセンテージ)法という表記法もあり, 上記のPU法を百分率で表したものである.
これから,このPU法を用いることで変圧器を含むシステムが驚くほどシンプルになることを確かめていこう.
理想的な変圧器へのPU法適用
まずは話を簡単にするため,理想的な2巻線変圧器にPU法を適用してみるところから始めよう.
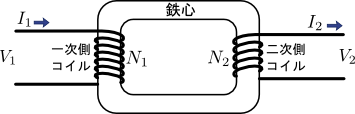
図1.理想的な2巻線変圧器(巻数比\(\frac{N_{1}}{N_{2}}\))
図1の変圧器が理想的であるということは,一次側電流\(I_{1}\)・一次側電圧\(V_{1}\)・二次側電流\(I_{2}\)・二次側電圧\(V_{2}\)との間で次の関係式を満たすと言い換えることができる.
これは,一次側と二次側の電圧比(変圧比)や電流比(変流比)は一定であり,巻数比により決定されるということを表している.それをより明示的に表した形式に上記の式を変形すると,
となる.たしかに変圧比,変流比が\(N_{1}\)と\(N_{2}\)によって表現されている.「この変圧器にPU法を適用すれば,単なる導線に変換できてしまう」と言うと,初めは驚かれるかもしれない.しかしよく考えると,PU法の適用に必要な基準電圧・基準電流も上記の関係式を満たすように設定できるので,それらの基準値からの比を表すPU法においては,一次側の電圧や電流は二次側の電圧や電流と等しくなるのである.
実際に,変圧器の基準電圧\(V_{base1}, V_{base2}\)と基準電流\(I_{base1}, I_{base2}\)が満たす関係についても明示しておこう.
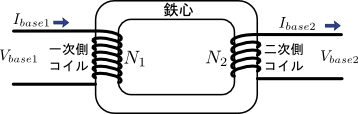
図2.変圧器の基準電圧・基準電流
図2には,PU法の適用に必要な基準電流や基準電圧が記入してある.一般的に\(V_{base1}\)は一次側の定格電圧,\(I_{base1}\)は一側の定格電流,\(V_{base2}\)は二次側の定格電圧,\(I_{base2}\)は二次側の定格電流が適用される.これらの間には,実際の電圧や電流と全く同じく,巻数\(N_{1}, N_{2}\)で決まる下記の関係を満たす.
ということは,式(4),式(5)と合わせれば
であることは容易に確かめられるだろう.これはつまり,定格電圧や定格電流を基準としてPU法を適用しただけで,一次側と二次側の間の電圧・電流が完全に等しくなるということである.すなわちPU法による電圧\(\overline{V_{1}},\overline{V_{2}}\),電流\(\overline{I_{1}},\overline{I_{2}}\)をそれぞれ
のように定義すると,基準値が式(7)と式(8)を満たす限り,
が成立するのである.ちなみに式(11)~(14)の割り算は,分子が実効値ならば分母の基準値も実効値による定格値とし,分子が波高値であれば分母も波高値による定格値とする.いずれにせよ,定格値のときに\(1 [p.u.]\)となるような定義がもっとも自然である.式(15)と式(16)から,次の図3のように,PU法を適用した後の変圧器は導線そのものに置き換え可能と言える.

図3.理想的な変圧器はPU法を用いると単なる導線と等価
この図3こそが,変圧器を含む電力網の解析にとってPU法が不可欠と言われる最大の理由である.電力網は数段階の電圧乗り換えを経て配電系に至るわけだが,それら異なる電圧系統間の電気的なやりとりも,PU法を使えば,あたかも同一電圧系統の問題として取り扱うことができるのである.現に図3の例においても,異なる電圧系統が事実上単一系統のように連結された.
それでは,今度はこの変圧器の前後にインピーダンス成分があった場合にはどのように扱われるのかを考えてみたい.まずはPU法を適用する前の状況から見ていこう.次の図4を見ていただきたい.

図4.インピーダンス\(Z_{1}\),\(Z_{2}\)を挿入したときの等価回路
図4の左側は理想変圧器(変圧比\(\frac{N_{1}}{N_{2}}\))の一次側にインピーダンス\(Z_{1}\),二次側にインピーダンス\(Z_{2}\)を挿入したものである.この回路を一次側から見たときの等価回路(一次側変換等価回路)は同図右側のようになる.一次側に挿入した\(Z_{1}\)はそのままのインピーダンスであり,一方二次側に挿入された\(Z_{2}\)は\(\left(\frac{N_{1}}{N_{2}}\right)^{2}\)倍されて一次側に変換される.
この例にPU法を適用したらどのように表されるだろうか.変圧器部分は単なる導線になるだろうが,インピーダンスの部分はどのように扱われるのだろうか?まずは図5を見ていただこう.

図5.図4にPU法を適用した場合
図5は図4にPU法を適用した場合の表現である.一次側・二次側ともに基準値(定格値)で割り算を行った後の\(p.u.\)値となっている.この場合,もはや二次側のインピーダンスを一次換算しないでも済む.例えば一次側に直列に挿入された\(0.1 [p.u.]\)のリアクタンスと二次側に直列に挿入された\(0.1 [p.u.]\)のリアクタンスはもはや区別されず,同じ電圧系統の同じリアクタンスとして扱われる.PU法を適用された後の系においては一次側/二次側の別に依らず\(p.u.\)値のみがすべてを語るのである.もちろん一次側のインピーダンス\(\overline{Z_{1}} [p.u.]\)をそのまま二次側に移したら,もはやインピーダンスは\(\overline{Z_{1}} [p.u.]\)ではないことに注意が必要である.ということで,ここで一度インピーダンスのPU法について定義しておく必要があるだろう.今までの定義と同じく,基準インピーダンス\(Z_{base1}, Z_{base2}\)を導入し,
と定義できる.ここで基準インピーダンス\(Z_{1}, Z_{2}\)は
と定義される.つまり,定格電流を流したら定格電圧の電位差を生むインピーダンスを\(1 [p.u.]\)と置くということである.また,今は単相交流を考えているが,もし三相交流であれば,線間電圧の定格値を\(V_{base}\),相電流を\(I_{base}\)にした場合
と,\(\sqrt{3}\)のファクターが分母に付くのが一般的となる.なお,\(V_{base}\)を線間電圧ではなく相電圧にすれば,この\(\sqrt{3}\)は不要となる.いずれにせよ,「定格電流を流したら定格電圧の電位差を生むインピーダンスを\(1 [p.u.]\)と置く」という原則に従えば,この\(\sqrt{3}\)というファクターも自然と導かれる.
ここまでで,理想的な変圧器を含む系にPU法を適用するとどうなるのか,大まかなイメージは湧いたことと思う.次の記事では,理想的でない変圧器(実際の変圧器)に対してPU法を適用したらどのように表されるのか等,PU法の実践的な適用例を紹介していく.
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.



 同機機のベクトル図(入門編)
同機機のベクトル図(入門編)






