架空送電線の理論1(導入編)

 

　本記事から，架空送電線の等価回路について考えていくことにしよう．ケーブルと同様，架空送電線の場合もキャパシタとインダクタの組み合わせで電気的な性質を表すことができる．つまり，架空送電線についても単位長さ当たりの静電容量とインダクタンスを求めることが目標になる．まずはこれまでのケーブルの計算結果を用いて，架空送電線の静電容量とインダクタンスを大まかに見積もることができないか考えてみよう．

　インダクタ等を大まかに見積もるだけでも，架空送電線の周りに生じる電磁界のイメージが全く湧かなければ手も足も出ない．というわけで次の図1に架空送電線の電磁界がどうなっているのか簡単に示した．

　

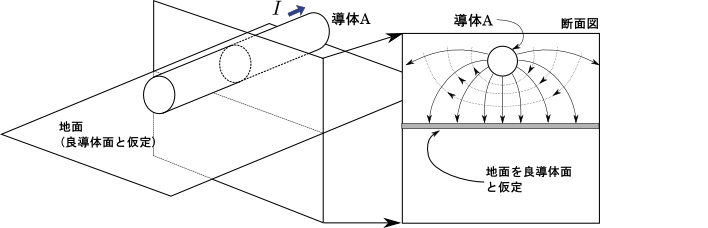
図1.架空送電線の周りの電磁界

 

 

　架空送電線（導体A）に電流が流れると，導体Aを周回するように磁界が生じる．また導体Aにかかっている電圧に比例して，地面に対する電界が生じる．この図1では地面が良導体面（つまり金属板のような，非常に低抵抗な面）であるとしている．実際の地面は金属板で置き換えられるほど電気伝導率は高くないため，この良導体面によるモデルは，下記の図2のように補正される．

 

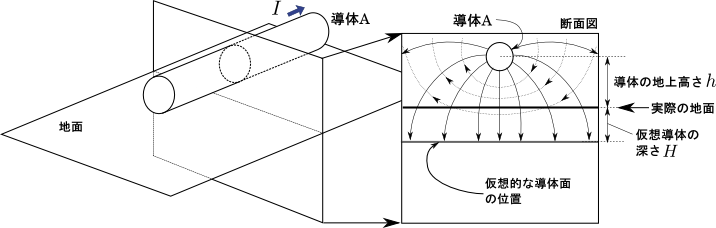
図2.実際の地面を良導体面で表現

 

 

　地面は，理想的な導体面として見立てるには余りにも電気伝導率が低いので，かなりの厚さ（それこそ数百m単位）の地面を以て理想導体面と近似する必要がある．つまり架空送電線が巻き起こす電磁界は地面によって完全に吸収されるわけだが，そのためには数百m以上の深さの大地を動員する必要があるのである．これは近似的には地表面よりも数百m下に理想的な導体面を置いた状況として表される．図2においてはその深さを\(H [m]\)としている．架空送電線の地上高さを\(h [m]\)とすると，架空送電線と仮想的な導体面との間の距離は\(h+H [m]\)となる．つまり，架空送電線の電磁気学的問題は，直線導体とその平行平板との問題に帰着できる．

　それではこの直線導体と平行平板の電磁気学的解析は簡単に実行可能なのだろうか？次の記事ではこれが割と簡単に計算できることを示すとして，ここでは前回までのケーブルでの計算結果を利用して，ざっくり静電容量とインダクタンスの見積もりを行ってみよう．

 

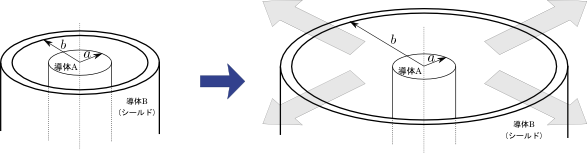
図3.ケーブルの計算結果を利用した架空送電線の\(L\),\(C\)見積もり

 

 

　まずは\(a\)は導体の半径であるから例えば\(a=0.01[m]\)（つまり\(1cm\)程度）としてみよう．では\(b\)の値をどうするか？ケーブルでは\(a\)のせいぜい2倍程度であったが，当然架空送電線の場合は導線のすぐ近くには他の導体はいないので，この\(b\)は\(a\)よりもはるかに大きな値を当てはめる必要がありそうだ．具体的には，図2で示した\(h+H\)くらいの値を入れるべきだろう．そして\(H\)は\(300\sim{900}[m]\)程度であることが知られているので，例えば大きめに見積もって\(b=1000 [m]\)を適用してみる．

　ここで，ケーブルの\(C\)と\(L\)の計算結果を思い出しておくと，

$$C = \frac{2\pi\epsilon}{\log\left(\frac{b}{a}\right)} \tag{1}$$
$$L=\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{b}{a}\right)\right] \tag{2}$$

これに，\(a=0.01[m]\)，\(b=1000 [m]\)を代入してみると， \(\epsilon\)と\({\mu}_{0}\)がそれぞれ真空誘電率と真空透磁率として

$$C = \frac{2\times{3.14}\times{8.853}\times{10^{-12}}}{\log\left(\frac{1000}{0.01}\right)} =6.4\times10^{-10} [F/m] $$
$$L=\frac{4\pi\times10^{-7}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{1000}{0.01}\right)\right] =2.4\times10^{-6} [H/m]$$

電力工学において一般的な単位である\(\mu{F}/km\)，\(mH/km\)に書き直すとそれぞれ\(0.64\mu{F}/km\)，\(2.4mH/km\)となる．それでは試しに\(a=0.01[m]\)，\(b=100 [m]\)を代入するとどうなるか？\(b\)の値を\(\frac{1}{10}\)にしても上記の式が\(\log\)なので値が余り変わらないことを確かめよう．

$$C = \frac{2\times{3.14}\times{8.853}\times{10^{-12}}}{\log\left(\frac{100}{0.01}\right)} =5.1\times10^{-10} [F/m] $$
$$L=\frac{4\pi\times10^{-7}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{100}{0.01}\right)\right] =1.9\times10^{-6}[H/m] $$

\(b\)の値を\(\frac{1}{10}\)にしても2割程度しか変わっていないことがわかるだろう．

 

　少なくとも，ケーブルの計算結果を用いたこれらの概算値は，精密に計算した静電容量や自己インダクタンスと大まかに一致する．次の記事では，架空送電線の正確な解析方法を学ぶとともに，そのことも同時に示していこう．

 

 

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス