ケーブルのインダクタンス計算

 

　前回の記事(ケーブルの静電容量計算)に引き続いて，本記事ではケーブルのインダクタンスを計算していこう．この記事の終盤において，ケーブルのインダクタンスは\(1km\)当たり\(0.1\sim{0.2} [mH]\)程度となることが理解できるだろう．前記事でも少し触れたが，電線のインダクタンスを計算したければ電線の周りに巻き起こる磁界を算出してやればよい．ということでまずは次の図1においてケーブルの磁界の様子を見てみよう．

 

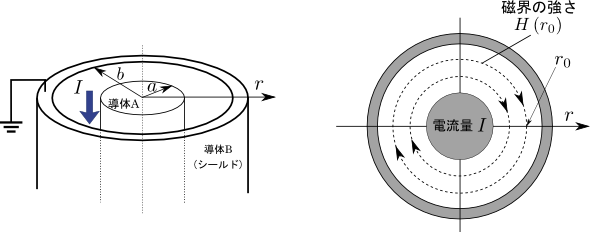
図1.ケーブルにおける磁界

 

 

　ケーブルに電流が流れると，電流を周回するように磁界が生じる．この磁界の強さ\(H\left({r}\right)\)は高校で習ったアンペールの法則を思い出せば

$$H\left({r}\right)=\frac{I}{2\pi{r}} \tag{1}$$

　磁界の強さは中心からの距離\(r\)の関数になっており，中心から離れるほどに小さくなることがわかる．実際中心からの距離\(r\)に対して磁界の強さをプロットすると次の図2のようになる．

 

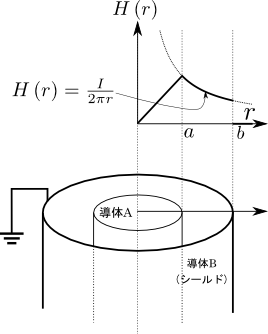
図2.ケーブルの周りに生じる磁界の強さ

 

 

　\(a\leq{r}\leq{b}\)の範囲では式(1)を満たすが，\(r\leq{a}\)，つまり導体A内における磁界は違う．詳しい議論は書籍などに譲るとして，ここでは結論だけを紹介しよう．導体Aの断面に一様の電流分布がある場合には\(r\leq{a}\)において\(H\left({r}\right)\)のグラフは直線となる．また\(r\geq{b}\)については\(H\left({r}\right)=0\)となる．これはケーブルのシールド（導体B）に逆向きの電流が流れて導体Aが起こす磁界を打ち消し，ケーブルの外の磁界はほぼ\(0\)になるからである．これらを総合すると，図2のようにケーブルの周りに生じる磁界の強さをプロットすることができる．

　ここまで来れば，インダクタンスの計算を開始することができる．ここでも結論から述べてしまうが，単位長さ当たりのインダクタンスというのは，下記の図3に示す面\(S_{0}\)を貫く磁束を計算することで求められる．

 

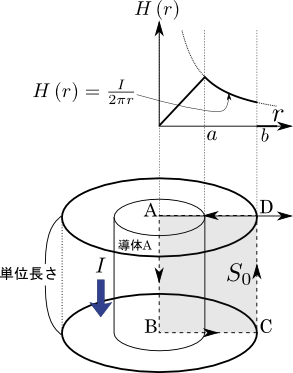
図3.ケーブルに対するファラデーの法則の適用

 

 

　これから我々は図3の面\(S_{0}\)に対してファラデーの法則を適用する．ファラデーの法則とは何だったか，この図3の例に適用しながら思い出して行こう．まずファラデーの法則を言葉で表すと，「ある閉回路に電磁誘導によって誘起される起電力は，その閉回路を鎖交する磁束の時間変化に等しい」というものであった．この図3の例に適用して言い直すと，「\(S_{0}\)を紙面に対して奥側から手前側へと貫く磁束の総和を\(\Phi\)とすれば，その時間変化の逆符号が\(S_{0}\)の境界を成す閉曲線一周分(\(A{\rightarrow}B{\rightarrow}C{\rightarrow}D{\rightarrow}A\))の起電力に等しい」となる．これを式にすると次の式(2)のようになる．

$$-\frac{d\Phi}{dt} = \oint_{A\rightarrow B\rightarrow C\rightarrow D\rightarrow A}\vec{E}\cdot{d}\vec{r}\tag{2}$$

ここで，\(\vec{E}\)は電界ベクトルである．この式の積分項は一見煩雑に見えるが，実は至ってシンプルである．なぜなら，積分区間\(B\rightarrow C\)と

\(D\rightarrow A\)の積分同士はケーブルの持つ電流方向の並進対称性から互いに打ち消し合い，また積分区間\(C\rightarrow D\)における積分は\(0\)になるため，結局積分区間\(A\rightarrow B\)しか残らないためである．つまり式(2)は，

$$-\frac{d\Phi}{dt} = \oint_{A\rightarrow B}\vec{E}\cdot{d}\vec{r}\tag{3}$$

まで単純化される．つまり\(A\)点から\(B\)点までの誘導起電力を\(V_{AB}\)とすれば，

$$V_{AB}=-\frac{d\Phi}{dt}\tag{4}$$

となる．あとはこの\(\Phi\)を求めることができれば，この式(4)を使って誘導起電力を求めることができるのである．そしていまや\(H\left({r}\right)\)の関数形が図3に示したように既知なので，\(\Phi\)は以下のように簡単に計算できる．

$$\begin{eqnarray*} \Phi&=&\int_{0}^{b}{\mu}_{0}H\left({r}\right)dr\\ &=&\int_{0}^{a}{\mu}_{0}H\left({r}\right)dr+\int_{a}^{b}{\mu}_{0}H\left({r}\right)dr\\ &=&\int_{0}^{a}{\mu}_{0}\frac{Ir}{2\pi{a^{2}}}dr+\int_{a}^{b}{\mu}_{0}\frac{I}{2\pi{r}}dr\\ &=&\frac{{\mu}_{0}I}{4\pi}+\frac{{\mu}_{0}I_{0}}{2\pi}\log\left(\frac{b}{a}\right)\\ &=&\frac{{\mu}_{0}I}{2\pi}\left[\frac{1}{2}+\log\left(\frac{b}{a}\right)\right] \tag{5} \end{eqnarray*}$$

ここで絶縁体の透磁率が真空の透磁率\({\mu}_{0}\)であると近似した．これを式(4)に代入すれば

$$\begin{eqnarray*} V_{AB}&=&-\frac{d\Phi}{dt}\\ &=& -\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{2}+\log\left(\frac{b}{a}\right)\right]\frac{dI}{dt} \tag{6} \end{eqnarray*}$$

ここで\(AB\)間のインダクタンス（つまり単位長さ当たりのインダクタンス）を\(L\)とすれば

$$V_{AB}=-L\frac{dI}{dt}\tag{7}$$

と書けるので，式(6)と式(7)を比較して

$$L=\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{2}+\log\left(\frac{b}{a}\right)\right]\tag{8}$$

 

これにて単位長さ当たりのケーブルのインダクタンスが計算できたように思われる．しかしこの結果は若干の補正をされなければならない．なぜなら，次の図4に示すように，ファラデーの法則を適用する閉回路の取り方により，インダクタンスの計算結果は式(8)から若干違った値となり，また閉回路として図3の取り方のみで正しいインダクタンスを算出することはできないからである．

 

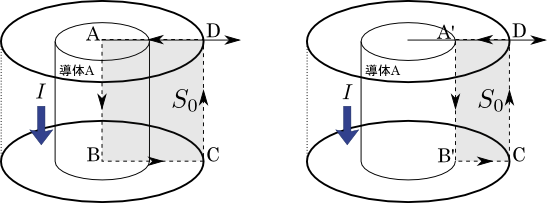
図4.ファラデーの法則を適用する閉回路面の違い

 

 

　いままでの計算は，図4の左側に示したような閉回路についてファラデーの法則を適用した場合であり，求められるインダクタンスは

$$L=\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{2}+\log\left(\frac{b}{a}\right)\right]\tag{8-再掲}$$

であった．一方，図4の右側に示したような閉回路についてファラデーの法則を適用した場合，\(0\leq{r}\leq{a}\)での磁束の積分がまるまる消失するため，式(8)の１項が丸々消えた形である

$$L=\frac{{\mu}_{0}}{2\pi}\log\left(\frac{b}{a}\right) \tag{9}$$

が求められるインダクタンスになる．現実のインダクタンスはこの両者の間のどこかの値になりそうな予想が立てられる．つまり，

$$L=\frac{{\mu}_{0}}{2\pi}\left[\alpha+\log\left(\frac{b}{a}\right)\right] (0\leq\alpha\leq\frac{1}{2}) \tag{10}$$

と書けそうである．この\(\alpha\)の値は導体Aを通じる電流の分布によって異なる．例えば高周波を通す場合は表皮効果のため電流が導体A表面に集中する．すると図4の右側のように導体A表面を通るような閉回路を設けて計算したときのインダクタンスこそ実際の電流が感じるインダクタンスと等しくなる．この場合式(9)が正確となり，式(10)の\(\alpha\)は\(0\)となる．一方で十分低周波の場合は導体Aに流れる電流の分布はほぼ一様になるので，そのときには\(\alpha=\frac{1}{4}\)，つまり式(8)と式(9)の丁度中間の値が実際のインダクタンスの値となる．イメージとしては中心を流れる電流は式(8)のインダクタンスを感じ，一方で導体A表面を流れる電流は式(9)のインダクタンスを感じるので，電流全体としてはその中間のインダクタンスが実際の値になるのだ．（このあたりの詳しい議論がどうしても知りたい場合は，電磁気学の専門書などを紐解いてもらいたい．）

　ということで，表皮効果が利くまでの周波数帯におけるケーブルの単位長さ当たりのインダクタンス\(L\)は，

$$L=\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{b}{a}\right)\right] \tag{11}$$

となる．

　この式(11)を見れば明らかなように，ケーブルのインダクタンスは\(\frac{b}{a}\)の値さえわかれば計算できる．例えば典型的な値として\(\frac{b}{a}=1.5\)を想定すると，真空透磁率\({\mu}_{0}=4\pi\times10^{-7}\)より式(11)は

$$L=\frac{4\pi\times{10^{-7}}}{2\pi}\left[\frac{1}{4}+\log\left(1.5\right)\right]\simeq{2}\times{10^{-7}}\left[\frac{1}{4}+0.405\right]=1.31\times10^{-7} [H/m]$$

と計算される．電力工学においては\([mH/km]\)が一般的な単位なので，その単位系に書き換えると\(0.131[mH/km]\)となる．大抵のケーブルは\(\frac{b}{a}\)の値が\(1.3\sim{2}\)の範囲に収まるため，同じように式(11)に代入して計算すればインダクタンスは\(0.102\sim{0.188}[mH/km]\)となる．大まかに言えば大体のケーブルが\(0.1\sim{0.2}[mH/km]\)のインダクタンスになることを示している．

　上記の計算は単心ケーブルであったが，三心ケーブルでも両者の正相インダクタンスの大きさとしては同じ程度になる．詳しくは書籍などで触れることにしよう．

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス