送電線と対称座標法

 

　本記事では対称座標法を実際の三相交流の送電線に適用して，あらゆる問題が非常に単純になることを示していく．その前に，前回の記事でも導入した対称座標法の定義をここでおさらいしておくことにしよう．

 

対称座標法のおさらい

 

　対称座標法とは，三相交流のa相・b相・c相の電気量である\(\left(V_{a}, V_{b}, V_{c}\right)\)から零相(0相)・正相(1相)・逆相(2相)の電気量である\(\left(V_{0}, V_{1}, V_{2}\right)\)へと式(1)を用いて線形変換したり，または逆に\(\left(V_{0}, V_{1}, V_{2}\right)\)から\(\left(V_{a}, V_{b}, V_{c}\right)\)へと式(2)を用いて線形的に逆変換することを用いた計算法のことである．

 

$$ \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix}=\boldsymbol{a} \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix} \tag{1} $$
$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}= \boldsymbol{a}^{-1} \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix} \tag{2} $$

ここで\(\boldsymbol{a}\)や\(\boldsymbol{a}^{-1}\)はともに\(3\times{3}\)の複素行列であり

$$ \boldsymbol{a}=\frac{1}{3} \begin{pmatrix} 1 & 1 & 1\\ 1 & a & a^{2}\\ 1 & a^{2} & a \end{pmatrix} \tag{3} $$
$$ \boldsymbol{a}^{-1}= \begin{pmatrix} 1 & 1 & 1\\ 1 & a^{2} & a\\ 1 & a & a^{2} \end{pmatrix} \tag{4} $$

ただし行列内の定数\(a\)は

$$a = \frac{-1+j\sqrt{3}}{2} \tag{5}$$

を満たす複素数であり，\(1\)の\(3\)乗根の1つである．ここでは電圧を例にとって説明をしたが，もちろんこれは電流でも皮相電力でも，三相交流の電気量であればなんでもよい．ただし，\(\left(V_{a}, V_{b}, V_{c}\right)\)も\(\left(V_{0}, V_{1}, V_{2}\right)\)も複素量である必要がある．したがって一般的には対称座標法はフェザー表示の電気量に用いられる計算手法である．もちろん数学的には

$$\boldsymbol{a}\boldsymbol{a}^{-1} = \boldsymbol{a}^{-1}\boldsymbol{a}= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} \tag{6}$$

は恒等的に成り立つ関係式なので，原理上は任意の\(\left(V_{a}, V_{b}, V_{c}\right)\)と\(\left(V_{0}, V_{1}, V_{2}\right)\)との間で対称座標法を適用することは可能であることを補足しておこう．それではこれから，この対称座標法を用いた送電線モデルの単純化を2例お見せしていく．

 

 

三相交流の静電容量と対称座標法

 

　まず，三相交流の送電線に下記の図1に示すような静電容量が付いている状況を考えよう．

　

 

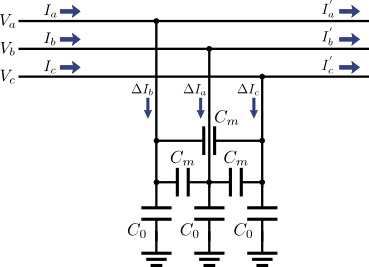
図1.三相交流送電線の静電容量

 

 

　図1では，線間容量\(C_{m}\)が各相線間について３つ，対地容量\(C_{0}\)が各相に対して３つ，それぞれ接続された形になっている．これらの容量に流れる電流の合計値\(\left(\Delta{I}_{a}, \Delta{I}_{b}, \Delta{I}_{c}\right)\)は，三相交流の電圧\(\left(V_{a}, V_{b}, V_{c}\right)\)を用いて，次のような式で表すことができる．

 

$$ \begin{pmatrix} \Delta{I}_{a}\\ \Delta{I}_{b}\\ \Delta{I}_{c} \end{pmatrix}=j\omega \begin{pmatrix} C_{0}+2C_{m} &-C_{m}& -C_{m}\\ -C_{m} &C_{0}+2C_{m}& -C_{m}\\ -C_{m} &-C_{m}& C_{0}+2C_{m} \end{pmatrix} \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix} \tag{7} $$

 

このように電圧\(\left(V_{a}, V_{b}, V_{c}\right)\)を線形変換することで容量に流れる電流\(\left(\Delta{I}_{a}, \Delta{I}_{b}, \Delta{I}_{c}\right)\)を求めることができる．この変換行列を\(\boldsymbol{G}\)とすると，上記の図1は次の図2のように書ける．

 

 

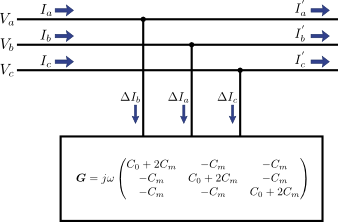
図2.図1のマトリックス表示

 

 

　この行列はすべての成分が\(0\)ではないので扱いにくい．ということで，この図2自体に対称座標法を適用してみよう．式(7)を\(\left(\Delta{I}_{0}, \Delta{I}_{0}, \Delta{I}_{0}\right)\)や\(\left(V_{0}, V_{1}, V_{2}\right)\)で表すべく，

 

$$ \begin{pmatrix} \Delta{I}_{a}\\ \Delta{I}_{b}\\ \Delta{I}_{c} \end{pmatrix}=\boldsymbol{a}^{-1} \begin{pmatrix} \Delta{I}_{0}\\ \Delta{I}_{1}\\ \Delta{I}_{2} \end{pmatrix} \tag{8} $$
$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}=\boldsymbol{a}^{-1} \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix} \tag{9} $$

 

を式(7)に代入すると，

 

$$ \boldsymbol{a}^{-1}\begin{pmatrix} \Delta{I}_{0}\\ \Delta{I}_{1}\\ \Delta{I}_{2} \end{pmatrix}=j\omega \begin{pmatrix} C_{0}+2C_{m} &-C_{m}& -C_{m}\\ -C_{m} &C_{0}+2C_{m}& -C_{m}\\ -C_{m} &-C_{m}& C_{0}+2C_{m} \end{pmatrix} \boldsymbol{a}^{-1}\begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix} $$

 

この式の左から\(\boldsymbol{a}\)を掛けると

 

$$ \begin{pmatrix} \Delta{I}_{0}\\ \Delta{I}_{1}\\ \Delta{I}_{2} \end{pmatrix}=j\omega \boldsymbol{a}\begin{pmatrix} C_{0}+2C_{m} &-C_{m}& -C_{m}\\ -C_{m} &C_{0}+2C_{m}& -C_{m}\\ -C_{m} &-C_{m}& C_{0}+2C_{m} \end{pmatrix} \boldsymbol{a}^{-1}\begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix} $$

 

この行列部分を\(\boldsymbol{G}_{012}\)と呼ぶと，

 

$$ \boldsymbol{G}_{012}=j\omega \boldsymbol{a}\begin{pmatrix} C_{0}+2C_{m} &-C_{m}& -C_{m}\\ -C_{m} &C_{0}+2C_{m}& -C_{m}\\ -C_{m} &-C_{m}& C_{0}+2C_{m} \end{pmatrix} \boldsymbol{a}^{-1}=j\omega\begin{pmatrix} C_{0} &0& 0\\ 0 &C_{m}& 0\\ 0 &0& C_{m} \end{pmatrix} \tag{10} $$

 

これは実際に式(3)～(5)を代入して計算すればこうなる．つまり，図2の状況は，対称座標法を適用することで次の図3のように書きなおせる．

 

 

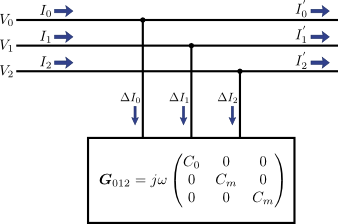
図3.図２に対称座標法を適用した場合

 

 

　この図3は対角行列なので，零相(0相)・正相(1相)・逆相(2相)は独立に扱えることを意味している．すなわち，対称座標法を適用すれば，図1のように三相の各相(a相・b相・c相)が複雑に絡み合っていた状態が，図4のように各相（0相・1相・2相）が独立に容量を持つ形に書き換えることができる．

 

 

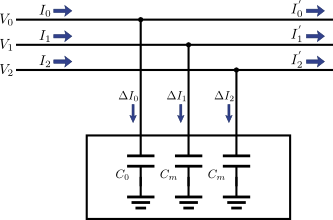
図4.図３を回路に戻したとき

 

 

このように，a相・b相・c相が絡み合っている系においても，十分ねん架されていてa相・b相・c相の交換対称性が成り立つ場合は，対称座標法を適用することで零相(0相)・正相(1相)・逆相(2相)間の相互作用が一切存在しない状態へと変換することができるのだ．次は同じように三相交流の各相に相互インダクタンスを含むケースについて，やはり対称座標法を適用することで問題を単純化できることを示そう．

 

 

三相交流のインダクタンスと対称座標法

 

　下記の図5に示すように，三相交流の各相に自己インダクタンス\(L_{s}\)と，各相間に相互インダクタンス\(L_{m}\)が付いている状況を考えよう．

　

 

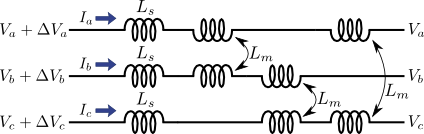
図5.三相交流送電線のインダクタンス

 

 

　a相・b相・c相のそれぞれに電流\(\left(I_{a}, I_{b}, I_{c}\right) \)が流れているとすると，この区間の三相交流の電位差\(\left(\Delta{V}_{a}, \Delta{V}_{b}, \Delta{V}_{c}\right)\)は，次のような式で表すことができる．

 

$$ \begin{pmatrix} \Delta{V}_{a}\\ \Delta{V}_{b}\\ \Delta{V}_{c} \end{pmatrix}=j\omega \begin{pmatrix} L_{s} &L_{m}& L_{m}\\ L_{m} &L_{s}& L_{m}\\ L_{m} &L_{m}& L_{s} \end{pmatrix} \begin{pmatrix} I_{a}\\ I_{b}\\ I_{c} \end{pmatrix} \tag{11} $$

 

このように電流\(\left(I_{a}, I_{b}, I_{c}\right)\)を線形変換することでこの区間の電位差\(\left(\Delta{V}_{a}, \Delta{V}_{b}, \Delta{V}_{c}\right)\)を求めることができる．この変換行列を\(\boldsymbol{Z}\)とすると，上記の図5は次の図6のように書ける．

 

 

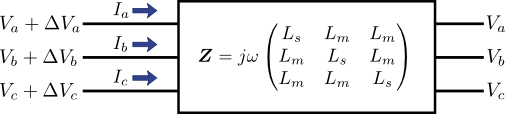
図6.図5のマトリックス表示

 

 

　この行列もまた，どの成分も\(0\)ではないので扱いにくい．ということで，この図6自体に対称座標法を適用してみよう．式(11)を\(\left(\Delta{V}_{0}, \Delta{V}_{0}, \Delta{V}_{0}\right)\)や\(\left(I_{0}, I_{1}, I_{2}\right)\)で表すべく，

 

$$ \begin{pmatrix} \Delta{V}_{a}\\ \Delta{V}_{b}\\ \Delta{V}_{c} \end{pmatrix}=\boldsymbol{a}^{-1} \begin{pmatrix} \Delta{V}_{0}\\ \Delta{V}_{1}\\ \Delta{V}_{2} \end{pmatrix} \tag{12} $$
$$ \begin{pmatrix} I_{a}\\ I_{b}\\ I_{c} \end{pmatrix}=\boldsymbol{a}^{-1} \begin{pmatrix} I_{0}\\ I_{1}\\ I_{2} \end{pmatrix} \tag{13} $$

 

を式(7)に代入すると，

 

$$ \boldsymbol{a}^{-1}\begin{pmatrix} \Delta{V}_{0}\\ \Delta{V}_{1}\\ \Delta{V}_{2} \end{pmatrix}=j\omega \begin{pmatrix} L_{s} &L_{m}& L_{m}\\ L_{m} &L_{s}& L_{m}\\ L_{m} &L_{m}& L_{s} \end{pmatrix} \boldsymbol{a}^{-1}\begin{pmatrix} I_{0}\\ I_{1}\\ I_{2} \end{pmatrix} $$

 

この式の左から\(\boldsymbol{a}\)を掛けると

 

$$ \begin{pmatrix} \Delta{V}_{0}\\ \Delta{V}_{1}\\ \Delta{V}_{2} \end{pmatrix}=j\omega \boldsymbol{a} \begin{pmatrix} L_{s} &L_{m}& L_{m}\\ L_{m} &L_{s}& L_{m}\\ L_{m} &L_{m}& L_{s} \end{pmatrix} \boldsymbol{a}^{-1}\begin{pmatrix} I_{0}\\ I_{1}\\ I_{2} \end{pmatrix} $$

 

この行列部分を\(\boldsymbol{Z}_{012}\)と呼ぶと，

 

$$ \boldsymbol{Z}_{012}=j\omega \boldsymbol{a} \begin{pmatrix} L_{s} &L_{m}& L_{m}\\ L_{m} &L_{s}& L_{m}\\ L_{m} &L_{m}& L_{s} \end{pmatrix} \boldsymbol{a}^{-1}=j\omega\begin{pmatrix} C_{0} &0& 0\\ 0 &C_{m}& 0\\ 0 &0& C_{m} \end{pmatrix} \tag{14} $$

 

これも実際に式(3)～(5)を代入して計算すればこうなる．つまり，図6の状況は，対称座標法を適用することで次の図7のように書きなおせる．

 

 

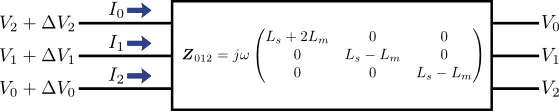
図7.図6に対称座標法を適用した場合

 

 

　静電容量のときと同様，インダクタンスにおいても零相(0相)・正相(1相)・逆相(2相)は独立に扱えることを意味している．すなわち，対称座標法を適用すれば，図5のように三相の各相(a相・b相・c相)が複雑に絡み合っていた状態が，図8のように各相（0相・1相・2相）が独立に容量を持つ形に書き換えることができる．

 

 

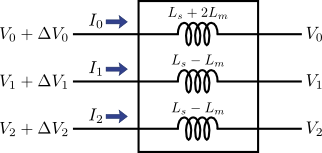
図8.図7を回路に戻したとき

 

 

このように，a相・b相・c相が絡み合っている系においても，十分ねん架されていてa相・b相・c相の交換対称性が成り立つ場合は，対称座標法を適用することで零相(0相)・正相(1相)・逆相(2相)間の相互作用が一切存在しない状態へと変換することができるのだ．このように，三相交流の配線容量やインダクタンスを考慮した解析を行いたい場合，対称座標法を適用すれば非常にシンプルな描像になることがわかるだろう．基本的に，図1や図5の想定は近似的に成り立つので，多くの三相交流の送電線においては，零相(0相)・正相(1相)・逆相(2相)のそれぞれが独立であるとして解析することができる．

　次の記事においては，上記に示した対称座標法の計算を応用して，簡単な例における三相短絡電流を計算してみよう．　

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス