架空送電線の理論2(計算編)

 

　本記事では架空送電線の静電容量とインダクタンスを正確に求めていこう．まずは架空送電線の周りにどのような電磁界が生じており，またそれらはどのように扱われればよいのか，図1でおさらいしてみる．

　

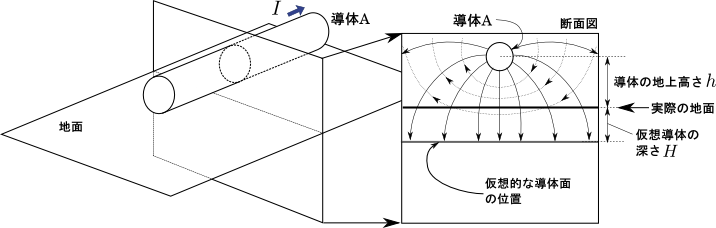
図1.架空送電線の周りの電磁界

 

 

　架空送電線（導体A）に電流が流れると，導体Aを周回するように磁界が生じる．また導体Aにかかっている電圧に比例して，地面に対する電界が生じる．図1で示している通り，地面は伝導体の平面として近似される．そしてその導体面は地表面から\(300{\sim}900\mathrm{m}\)程度潜った位置にいると考えると，実際の状況を適切に表すことができる．このように，架空送電線の電磁気学的な解析は，送電線と仮想的な導体面との間の電磁気学と置き換えて考えることができるのである．

　その送電線と導体面との距離は，次の図2に示すように，送電線の地上高さ\(h\)と仮想導体面の地表深さ\(H\)との和である，\(H+h\)で表される．

 

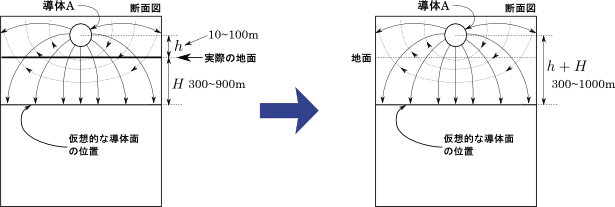
図2.実際の地面を良導体面で表現

 

 

　そして\(H\)の値は\(300{\sim}900\mathrm{m}\)程度，また\(h\)の値は一般的に\(10{\sim}100\mathrm{m}\)程度となろう．ということは地上を水平に走る架空送電線は，完全導体面の上を高さ\(300{\sim}1000\mathrm{m}\)程度で走っている導体と電磁気学的にはほぼ等価であると言える．

　それでは，導体面と導線の２体による電磁気学をどのように計算するのか，次の図3を見て頂きたい．

 

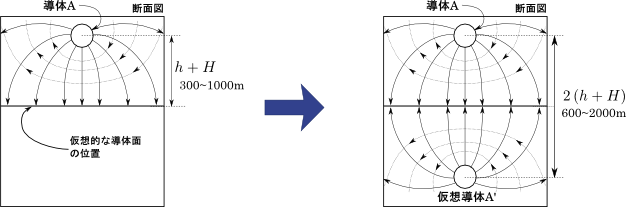
図3.鏡像法を用いた図2の解法

 

 

　図3は，鏡像法という解法を示している．つまり，導体面そのものを電磁的に扱うのではなく，むしろ導体面は取っ払って，その代わりに導体面と対称の位置に導体Aと同じ大きさで電荷や電流が反転した仮想導体A’を想定している．導体面を鏡と見立てたとき，この仮想導体A'は導体Aの鏡像そのものであり，導体面をこのような鏡像に置き換えて解析しても全く同一の電磁気学的結果を導けるのである．この解析手法のことを鏡像法と呼んでおり，今回の解析の要である．

　ということで鏡像法を用いると，図4に示すように\(2\left({h+H}\right)\)だけ離れた平行2導体の問題に帰着できる．

 

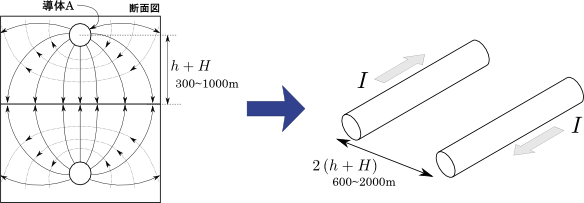
図4.鏡像法を利用した架空送電線の問題簡略化

 

 

　あとはこの平行2導体の電磁気学を展開すればよい． 具体的には，下記の図5のような断面を持つ平行2導体の静電容量とインダクタンスを求めてあげればよい．

 

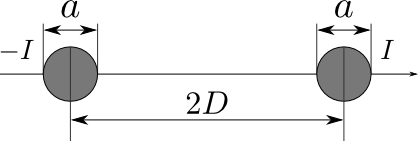
図5.解析対象となる並行2導体

 

 

　この問題は，ケーブルの静電容量やインダクタンスの計算のときに用いた物理法則（ガウスの法則・アンペールの法則・ファラデーの法則）を適用することにより，\(a\ll 2D\)の状況においては次のように解くことができる．

$$C = \frac{2\pi{\epsilon}_{0}}{\log\left(\frac{2D-a}{a}\right)} \tag{1}$$
$$L=\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{2D-a}{a}\right)\right] \tag{2}$$

ここで，\(\epsilon_{0}\)と\(\mu_{0}\)はそれぞれ真空誘電率と真空透磁率である．それではこれに架空送電線の値を当てはめてみる．図4により，\(D=h+H\)であるから

$$C \simeq \frac{2\pi{\epsilon}_{0}}{\log\left(\frac{2\left({h+H}\right)}{a}\right)} \tag{3}$$
$$L\simeq\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{2\left({h+H}\right)}{a}\right)\right] \tag{4}$$

ここで\({h+H-a}\simeq{h+H}\)を使った．これで単位長さ当たりの架空送電線の静電容量（対地）と自己インダクタンスが求められた．ケーブルの結果と見比べると，\(b\)が\(2\left({h+H}\right)\)に置き換わっただけであることに気付くだろう．

 

　これまでの解析では，架空送電線は大地上を単線で敷かれているとしてきたが，実際の架空送電線は三相交流を送電している場合が一般的であるから，最低３本の導線が平行して走っているケースが解析できなければ意味がない．ということで，その準備としてまずは２本の電線が平行して走っている状況を同様に解析してみよう．下記の図6を見て頂きたい．

 

図6.2本の架空送電線

 

 

　並走する架空送電線が２本だけでは，３本の解析には応用できないのではないかという心配を持たれるかもしれないが，問題ない．なぜならこの２本での相互インダクタンスや相互静電容量の計算結果を適切に組み合わせることにより，３本以上の導線の解析にも簡単に拡張することができるからである．図6の左側は今までの単線での想定そのものであり，一方でこれから考えるのは図6の右側，つまりa相の電線と平行にb相の電線が走っている状況である．このときのa相とb相との間の静電容量\(C_{ab}\)と相互インダクタンス\(L_{ab}\)を求めてみよう．

　今までと同じように物理法則（ガウスの法則・アンペールの法則・ファラデーの法則）を適用することにより，下記のような計算結果を得る．

$$C_{ab} \simeq \frac{2\pi{\epsilon}_{0}}{\log\left(\frac{d_{{a}'b}}{d_{ab}}\right)} \tag{5}$$
$$L_{ab}\simeq\frac{{\mu}_{0}}{2\pi}\log\left(\frac{d_{{a}'b}}{d_{ab}}\right) \tag{6}$$

この結果は，図5のときの結果である式(1)や式(2)からも簡単に導かれる．a相とa'相は互いに逆符号の電流と電荷を持っており，b相への影響の符号は反対であるから，例えば上記の式(6)を求めたければ，a相とb相の組についての式(2)とa'相とb相の組についての式(2)の差を取ってやればよいことがわかる．実際は下記のような計算となる．

$$L_{ab}=\frac{{\mu}_{0}}{2\pi}\left[\left(\frac{1}{4}+\log\left(\frac{2d_{{a}'b}-a}{a}\right)\right)-\left(\frac{1}{4}+\log\left(\frac{2d_{ab}-a}{a}\right)\right)\right]\simeq\frac{{\mu}_{0}}{2\pi}\log\left(\frac{d_{{a}'b}}{d_{ab}}\right)$$

これで式(6)と一致していることがわかるだろう．式(5)についても同様に式(1)の組み合わせで計算できる．

 

いずれにせよ，ここで述べたかったことは，大地上を平行に走る２線間の静電容量やインダクタンスは\(d_{ab}\gg a\)の条件下において正確に計算できるということであった．この結果を三相交流の架空送電線に適用してみよう．十分に捻架されているケースではa,b,c相間の各相間容量や相互インダクタンスは等しく，a,b,c相それぞれが持つ対地容量や自己インダクタンスも等しい．よって，相間容量を\(C_{m}\)，各相間の相互インダクタンスを\(L_{m}\)，１相当たりの対地容量を\(C_{s}\)，自己インダクタンスを\(L_{s}\)と置くと，上記の式(3)，(4)，(5)，(6)を適用して，

$$C_{s} \simeq \frac{2\pi{\epsilon}_{0}}{\log\left(\frac{2\left({h+H}\right)}{a}\right)} \tag{7}$$
$$L_{s}\simeq\frac{{\mu}_{0}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{2\left({h+H}\right)}{a}\right)\right] \tag{8}$$
$$C_{m} \simeq \frac{2\pi{\epsilon}_{0}}{\log\left(\frac{2\left({h+H}\right)}{d_{ab}}\right)} \tag{9}$$
$$L_{m}\simeq\frac{{\mu}_{0}}{2\pi}\log\left(\frac{2\left({h+H}\right)}{d_{ab}}\right) \tag{10}$$

ここで，\(h\)はa,b,c相の地上高さ，\(a\)は各導線の直径である．また式(9)，(10)については\(d_{{a}'b}\simeq{2\left({h+H}\right)}\)という近似を用いた．これにより，三相交流の導線についても単位長さ当たりの静電容量とインダクタンスが，相間のものも含めてすべて計算できた．文献によっては式(7)と式(9)の静電容量の式は，実際の地面を等電位面とした\(H=0\)（つまり理想導体面と地面の高さが一致）を適用しているが，交流の静電容量の場合は地面は等電位面ではないので，上記の式(7)や式(9)から\(H\)を除かない方がより正確である（計算結果に大きな差は生まない）．これらの式に典型的な値を入れてみよう．\(2\left({h+H}\right)=1000\)，\(d_{ab}=10\)，\(a=0.02\)としてみる．すると，

$$C_{s} \simeq \frac{2\times{3.14}\times{8.853}\times{10^{-12}}}{\log\left(\frac{1000}{0.02}\right)}\simeq{5.14}\times10^{-12} \mathrm{F/m}$$
$$L_{s}\simeq\frac{4\pi\times10^{-7}}{2\pi}\left[\frac{1}{4}+\log\left(\frac{1000}{0.02}\right)\right]\simeq{2.21}\times{10^{-6}} \mathrm{H/m}$$
$$C_{m} \simeq \frac{2\times{3.14}\times{8.853}\times{10^{-12}}}{\log\left(\frac{1000}{10}\right)}\simeq{1.21}\times10^{-11} \mathrm{F/m}$$
$$L_{m}\simeq\frac{4\pi\times10^{-7}}{2\pi}\log\left(\frac{1000}{10}\right) \simeq{9.71}\times{10^{-7}} \mathrm{H/m}$$

これらの結果によれば，１相当たりの対地容量は約\(0.005\mu\mathrm{F/km}\)，自己インダクタンスは約\(2\mathrm{mH/km}\)，相間容量は約\(0.01\mu\mathrm{F/km}\)，相互インダクタンスは約\(1\mathrm{mH/km}\)であることがわかった．次に説明する対称座標法を導入するとわかるが，正相インダクタンスは自己インダクタンス約\(2\mathrm{mH/km}\)ー相互インダクタンス約\(1\mathrm{mH/km}\)＝約\(1\mathrm{mH/km}\)と求められる．

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス