変圧器の動作イメージ
本記事では,変圧器がざっくりどのような電気的性質を持っているのか,そのイメージを簡単に説明していくことにしよう.変圧器の物理的原理も含めた理論的裏付けは次の記事で行うこととする.この変圧器の動作イメージの説明に入る前に,今回から扱っていく交流変圧器(以下,単に変圧器と呼ぶ)の仕組みを簡単におさらいしておく.次の図1を見て頂きたい.
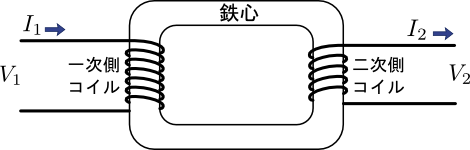
図1.変圧器の仕組み
このように,一次側コイルと二次側コイルとが同じ鉄心に巻きつけられており,お互いが磁気的に結合している電気機械となっている.一次側コイルと二次側コイルは,この磁気的な結合を介して交流電力を渡し合っているのである.「磁気的結合で間接的につながっているだけだから,エネルギーはほとんど伝わらないのでは?」という疑問も出そうだが,結論から言えばロスは\(数\%\)以下である.それほどまでに磁気を介した電力伝達には無駄がないのだ.
それでは次に,この変圧器が具体的にどのような電気的性質を持っているのか,次の図2のように電圧や電流に着目しつつ考えてみることにしよう.
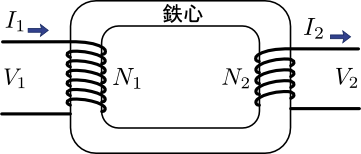
図2.巻数比\(\frac{N_{1}}{N_{2}}\)の変圧器
上記の図2のように,一次側コイルと二次側コイルの電流・電圧に着目してみる.ここで,一次側コイルの巻数を\(N_{1}\),二次側コイルの巻数を\(N_{2}\)とした.実はこの巻数(正確には巻数比)こそが,変圧器の電気的特性を特徴づける非常に大事な量となっている.実際次の式(1)と式(2)が,この変圧器が満たす電気的特性となっている.
確かに\(N_{1}\)と\(N_{2}\)とで電気的特性が決まっている.この物理的な理屈は次の記事で説明するとして,ここではこの式のイメージを膨らませていきたい.この式を力学系に喩えてみると,例えば次のようなテコの問題と対応づけることができるだろう.
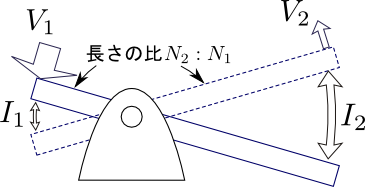
図3.変圧器をテコの問題に喩えた場合
図3におけるテコの始点から見た柄の長さの比は\(N_{2}:N_{1}\)であるから,左右の移動速度をそれぞれ電流\(I_{1}\)・\(I_{2}\)に対応させ,左右に加わっている力をそれぞれ電圧\(V_{1}\)・\(V_{2}\)に対応させればまさに
が成立する.これは変圧器の電気的特性を表した式(1)・式(2)と同一である.変圧器というのは力学の世界で言えば単なるテコないしは変速機のようなものであり,基本特性は非常にシンプルと言える.
次に,変圧器の電流や電圧がどのように決まるのか,そのイメージを簡単に浮かべてみよう.上記の式(1)・式(2)は変圧器の一次側と二次側の関係を結んでいるだけであり,当然ながらこれらの式だけでは変圧器に加わる電圧・電流を特定することはできない.周りの状況に100%依存するのである.これを理解するために便利な例を次の図4に用意した.

図4.巻数比\(1\)の変圧器と等価回路
この図4は一次側と二次側の巻数が等しいケース,つまり巻数比が\(1\)の場合を示しており,式(1)・式(2)から
が成り立つ.左右の電流と電圧が一致しているので,これはまさに導線そのものである.すなわち図4の右側のように表すことができる(実際はわずかな漏れインダクタンスが直列に付くが,ここでは無視する).これからも明らかなように変圧器というのは単なる導線のようなものなので,その電流や電圧は100%周りの状況により決定される.式(1)や式(2)は単に右と左を関連付けているだけなので当然と言えば当然である.これは巻数比が\(1\)以外のときにも同様のことが言える.PU法という計算手法を導入すれば,任意の巻数比の変圧器が単なる導線のように扱われることが示されるのである.このPU法の概要は今後の記事で,また詳細は書籍などで触れる.
次に,変圧器が実質的に単なる導線であるという物理的イメージをより深く理解するため,下記の図5のように二次側を開放させたケースを考えてみよう.

図5.二次側が開放のとき
二次側が開放されているので二次側の電流は\(0\),つまり\(I_{2}=0\)である.変圧器が単なる導線として振る舞うのであれば一次側の電流\(I_{1}\)も\(0\)になるはずである.実際式(2)に\(I_{2}=0\)を代入しても\(I_{1}=0\)が得られるが,本当に一次側の電流も\(0\)になるのだろうか?一次側コイルが断線しているわけでもないのに電流\(0\)というのはどういうことか?
結論から言ってしまうと,鉄心に磁場を起こすために必要な,変圧器が通常時に扱う負荷電流などに比べると非常に小さい電流(励磁電流)が流れる.この励磁電流が通常無視できるくらい小さい電流として扱えるから,
という関係が成り立っているのだということを強調しておきたい.励磁電流というのを図3で示したテコの例に当てはめると,テコの柄の微小な変形に対応づけられる.しかしざっくり見ればテコはほとんど形を変えないので,上記の式(2)が近似的に成り立つということになるのである.
変圧器の物理的振る舞いが大体イメージできたところで,最後に変圧比・変流比・巻数比の関係について整理しておこう.
変圧比と巻数比は同じであり,これらと変流比は逆数の関係にある.上記までの議論からもわかるように,変圧比というのはテコや変速機などの例におけるギア比になっている.
ここまでで変圧器の電気的特性についてある程度のイメージが湧いたことと思う.次の記事においては何故このような特性が磁気的結合によって達成されるのか,その物理的な原理を解説することにしよう.
News!!
☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました!
☆【入門演習 パワーエレクトロニクス】も好評発売中です!試読はこちらから。
Copyright © 2017 EnergyChord. All rights reserved.



 同機機のベクトル図(入門編)
同機機のベクトル図(入門編)






