変圧器の物理的原理

 

　ここからは変圧器の原理を物理法則まで立ち返って説明していこう．変圧器の動作イメージがいまいち湧かない場合はまず前回の記事「変圧器の動作イメージ」から読まれるとよいだろう．それでは早速内容に入っていきたい．はじめに，変圧器の電気的特性がどのようなものだったか，次の図1を例にとっておさらいしよう．

　

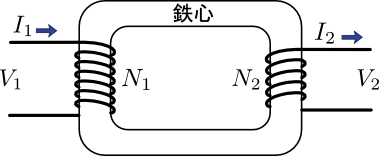
図1.変圧比が\(\frac{N_{1}}{N_{2}}\)の変圧器

 

 

　図1で示した変圧器が満たす電気的特性は，次の式(1)と式(2)で表される．

$$V_{1}:V_{2} = N_{1}:N_{2} \tag{1}$$
$$I_{1}:I_{2} = N_{2}:N_{1} \tag{2}$$

　これがどのような物理的イメージとつながるのかは前回話したので，今回はなぜこのような式が成立するのか，その根底にある物理法則から説明していくことにしよう．まずは鉄心の磁束から考えなければ何も始まらないので，次の図2に示すように鉄心を通る磁束を\(\Phi\)とおく．

 

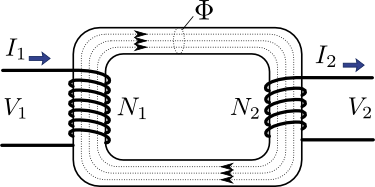
図2.巻数が\(N_{1}\)，\(N_{2}\)の変圧器と磁束\(\Phi\)

 

 

　磁束\(\Phi\)を定義すると，ファラデーの法則から，下記のように電圧\(V_{1}\)，\(V_{2}\)を求めることができる．

$$V_{1} = N_{1}\frac{d\Phi}{dt} \tag{3}$$
$$V_{2} = N_{2}\frac{d\Phi}{dt} \tag{4}$$

一次側コイルと二次側コイルを貫く磁束が完全に同じ\(\Phi\)であれば（つまり漏れ磁束が\(0\)ならば），上記の２式のように\(\frac{d\Phi}{dt}\)の部分が完全に共通となるので，電圧比は純粋に巻数の比となることがわかる．

$$V_{1}:V_{2} = N_{1}\frac{d\Phi}{dt}:N_{2}\frac{d\Phi}{dt} = N_{1}:N_{2} $$

これは式(1)そのものである．つまり言い換えると，式(1)を満たすためには鉄心の磁束\(\Phi\)に対して漏れ磁束が十分小さく，一次側コイルと二次側コイルが近似的に同一の磁束をシェアしていればよいということが言える．ここで一応この磁束\(\Phi\)がどのように決まるのか，少し考えてみることにしよう．

 

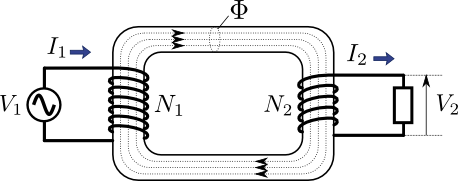
図3.鉄心の磁束\(\Phi\)の決まり方

 

 

　式(3)や式(4)を見れば明らかだが，コイルの起電力が分かれば自動的に\(\Phi\)も求められることがわかる．例えば式(3)を用いて\(\frac{d\Phi}{dt}\)について解いてあげれば，

$$\frac{d\Phi}{dt} = \frac{V_{1}}{N_{1}}$$

これを積分して，

$$\Phi\left({t}\right) = \frac{1}{N_{1}}\int_{0}^{t}V_{1}\left({\tau}\right)d\tau+\Phi\left({0}\right) \tag{5}$$

\(\Phi\)というのは，このように電圧の積分として表すことができる．そして通常の交流変圧器においては電圧が正弦波で表すことができるため，その積分である磁束\(\Phi\)も正弦波となる．図3のケースでは\(V_{1}\)が電圧源により完全に決まっているので，この電圧源の\(V_{1}\)を純粋に積分してやればよい．

　ここまでで，電圧と磁束の関係について，ある程度のイメージが湧いたことと思う．次は電流と磁束の関係について考えてみることにしよう．電流に巻数を掛けたものを起磁力といい，磁束の発生に必要なものであることを，次の図4で示したい．

 

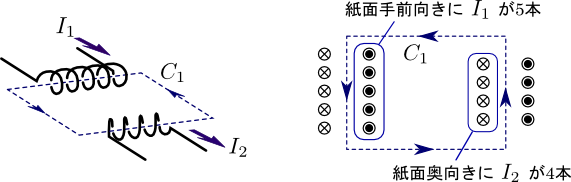
図4.アンペアの周回積分を変圧器に適用

 

 

　上記の図4は，変圧器を単純化させたもので，ループ経路\(C_{1}\)は磁束の通り道（つまり鉄心）を表している．この\(C_{1}\)に２つのコイルが巻き付いており，一つが巻数\(5\)で電流\(I_{1}\)，もう一つが巻数\(4\)で電流\(I_{2}\)としたときに，この経路\(C_{1}\)に起きる起磁力は，

$$ 5I_{1}-4I_{2}$$

と表される．起磁力というのは，この経路\(C_{1}\)に沿ってどれくらいの磁界を発生させることができるのかを表しており，具体的には下記のような周回積分(閉じた経路の線積分1周分)との等式が成立する．

$$ 5I_{1}-4I_{2}=\int_{C_{1}}\vec{H}\left(\vec{r}\right)\cdot{d\vec{r}} \tag{6}$$

線積分が出てきて混乱する方も安心していただきたい．この式が持つ物理的意味は極めてシンプルである．要するに\(C_{1}\)に沿って磁界\(\vec{H}\)の経路方向成分と長さを掛け合わせながら一周分足し合わせたものである．この式は，アンペアの周回積分と呼ばれる．経路\(C_{1}\)を貫く電流の総量と，磁界\(\vec{H}\)の\(C_{1}\)上での周回積分が等しくなるという定理である．

　ここからは，鉄心という極めて透磁率の高い物質を用いていることを考慮することで，この式(6)の値がほぼ\(0\)にならざるを得ないということを説明したい．このことを理解するには，鉄心の磁化曲線（下記の図5）を思い出す必要がある．

 

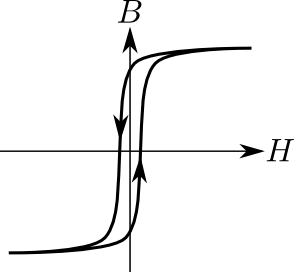
図5.鉄心の磁化曲線

 

 

　鉄心の透磁率が高いということは，極めて小さな磁界の大きさ\(H\)で大きな磁束密度\(B\)を達成できるということになる．実際上記の図5は，小さな\(H\)の値で大きく磁束密度\(B\)が変化し飽和に至るということを示している．一方で変圧器に与えられる電圧から鉄心の磁束\(\Phi\)は式(5)のように決定されるため，磁束密度\(B\)もおのずと決まる．ここで例えばこの磁束密度\(B\)が，下記の正弦波に示したような範囲で振動するようなものだった場合，磁化曲線から逆算して鉄心の磁界の大きさ\(H\)は水色の範囲，つまり\(\Delta{H}\)の幅を持つ範囲内に収まることになる．

 

図6.磁化曲線から逆算した磁界の大きさの範囲\(\Delta{H}\)

 

 

　この\(\Delta{H}\)が十分小さいとすると，\(H<\Delta{H}\)より式(6)は

$$ 5I_{1}-4I_{2}=\int_{C_{1}}\vec{H}\left(\vec{r}\right)\cdot{d\vec{r}}\simeq0 \tag{7}$$

となる．実際はわずかな電流（励磁電流）が流れているのだが，それは通常の負荷電流\(I_{1}\)や\(I_{2}\)よりもはるかに小さいと考えてよい．これにより，

$$ I_{1}:I_{2}\simeq{4:5} $$

が成立することがわかる．これこそが式(2)そのものとなっている．式(2)は励磁電流が小さいときに成り立つ近似式であることに注意しよう．

　それではこれまでの計算をもう一度下記の一般的な変圧器について計算しなおしてみよう．

 

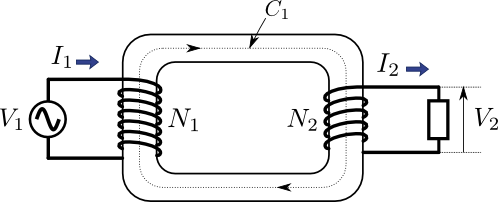
図7.巻数が\(N_{1}\)，\(N_{2}\)の変圧器

 

 

　鉄心に沿ったある経路\(C_{1}\)について，起磁力は

$$ N_{1}I_{1}-N_{2}I_{2}$$

となる．よってアンペアの周回積分は，

$$ N_{1}I_{1}-N_{2}I_{2}=\int_{C_{1}}\vec{H}\left(\vec{r}\right)\cdot{d\vec{r}} \tag{8}$$

となる．今回経路\(C_{1}\)は右回りなので，電流は\(C_{1}\)の内部を紙面奥側に貫く場合に正とした．鉄心の透磁率は極めて高いため鉄心の磁化が飽和に至っていない限り\(H\)は非常に小さなものとなっている．よって式(8)から

$$ N_{1}I_{1}-N_{2}I_{2}\simeq{0} \tag{9}$$

と言える．これを変形して

$$ I_{1}:I_{2}\simeq{N_{2}:N_{1}} \tag{10}$$

こうして一般的な例においても式(2)を示すことができた．通常動作時には式(9)がよい近似として成立することがカギとなっている．実際この関係が破れるときがあり，それは鉄心が飽和領域に突入してしまったときである．変圧器に非常に大きな電圧を加えたり，規格外の低周波を与えたり，または通常の電圧・周波数であっても初期状態が強く磁化した状態であれば鉄心の飽和は起こり得る．そして鉄心が飽和に至ってしまうと大きな突入電流が流れる．これらを理解するためにも，上記で議論した物理的原理がベースとなるので，しっかりと押さえておいてもらいたい．

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス