ケーブルの静電容量計算

 

　前回の記事において送電線が（ケーブルか架空送電線かに関わらず）インダクタとキャパシタンスの組み合わせにより等価回路を構成できることを示した．本記事と次の記事ではそのうちケーブルに的を絞り，単位長さ当たりのケーブルが持つ寄生インダクタンスとキャパシタンスの値について具体的に計算してみることにしよう．今回は静電容量の計算について解説する．この記事の最後には，ケーブルの静電容量が\(0.2\sim{0.5}[\mu{F}/km]\)程度になることが示されるだろう．

　これからの計算には，次の記事（インダクタンスの計算）も含め電磁気学の法則を用いるため，まずケーブル内の電界と磁界の様子を簡単におさらいしておくと話を進めやすい．次の図1は交流を流しているケーブルの断面における電界と磁界の様子を示している．

 

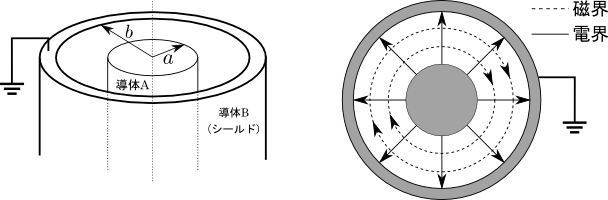
図1.ケーブルにおける電磁界

 

 

　まず，導体Aが長さ当たりに持つ電荷の量に比例して電界が放射状に発生する．電荷量と電界の強さとの間の関係が分かれば単位長さ当たりのキャパシタンスを計算できる．つまり，今回の計算では電界の強さを求めることがポイントになる．

　また，導体Aが流す電流の大きさに比例して導線を取り囲むような同心円状の磁界が発生する．電流量と磁界の強さとの間の関係が分かれば単位長さ当たりのインダクタンスを計算できる．これは，次回の記事において説明する．

　それでは早速ケーブルのキャパシタンス（以下静電容量と言い換える）を計算していくことにしよう．単位長さのケーブルに寄生する静電容量を求めるため，図2に示すように単位長さ当たり\(q[C]\)の電荷をケーブルに与えてみる．

 

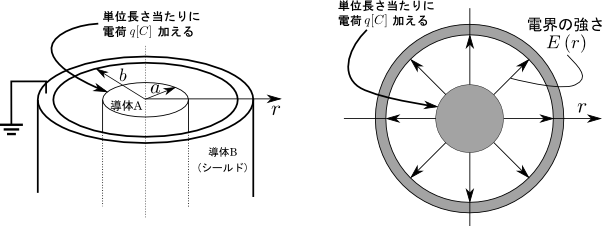
図2.単位長さ当たりに電荷\(q[C]\)を与えたケーブル

 

 

　ケーブルに電荷を与えると，図2の右側に示すように，電界が放射状に発生する．この電界の強さは中心からの距離\(r\)の関数になっている．なぜならケーブルが軸に対して回転対称であるから，距離\(r\)が定まればそこでの電界の強さ\(E\left({r}\right)\)も一意的に定まるのである．

　そしてこの電界の強さ\(E\left({r}\right)\)の関数形が分かれば，簡単にケーブルの静電容量も計算できる．なぜなら，電界の強さ\(E\left({r}\right)\)を\(r\)に対して\([a.b]\)の区間で積分すれば，それは導体Aと導体Bの間の電位差\(V_{AB}\)と言えるからである．

$$V_{AB} = \int_{a}^{b}E\left({r}\right)dr \tag{1}$$

そしてこの電位差\(V_{AB}\)が分かれば，単位長さ当たりの電荷\(q\)との比を取ることにより，単位長さ当たりの静電容量\(C\)を求めることができる．

$$C = \frac{q}{V_{AB}} \tag{2}$$

よって，ケーブルの静電容量を求める問題は，電界の強さ\(E\left({r}\right)\)の関数形を知るという問題となる．この電界の強さ\(E\left({r}\right)\)を計算するためにはガウスの法則という電磁気学的な法則を使う．これから下記の図3についてガウスの法則を適用していこう．

 

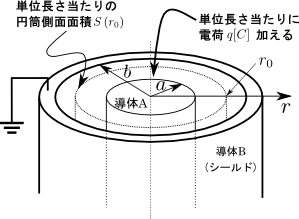
図3.ケーブルに対するガウスの法則の適用

 

 

　図3は，図2の状況（ケーブルに単位長さ当たり\(q\)の電荷を加えた状況）において半径\(r_{0}\)の円筒面を考えたものである．ガウスの法則というのは，「ある閉曲面を貫く電束は，その閉曲面内の電荷の総和に等しい」という電磁気学の法則である．この法則を図3の半径\(r_{0}\)で単位長さの円筒について適用してみる．円筒の側面における電界の強さは\(E\left({r_{0}}\right)\)であるから，そこでの電束密度は導体Aと導体Bの間を満たす誘電体の誘電率\(\epsilon\)を掛けた\({\epsilon}E\left({r_{0}}\right)\)となる．そして電束ベクトルは電界と同じく円筒側面と垂直であるから，円筒側面の面積を\(S\left({r_{0}}\right)\)とすると，円筒側面を貫く電束は

$$\epsilon{E\left({r_{0}}\right)}S\left({r_{0}}\right) \tag{3}$$

そして，円筒の底面と上面を貫く電束が\(0\)であることを使えば，円筒全体を貫く電束が上記(3)そのものであることがわかる．ここでガウスの法則を適用すれば，式(3)が円筒内の電荷\(q\)になるため(ここでの円筒の長さは単位長さなので)，

$$q=\epsilon{E\left({r_{0}}\right)}S\left({r_{0}}\right) \tag{4}$$

これにより，電界の強さ\(E\left({r_{0}}\right)\)が計算でき，

$${E\left({r_{0}}\right)}=\frac{q}{\epsilon{S\left({r_{0}}\right)}} \tag{5}$$

ここで，円筒側面の面積\(S\left({r_{0}}\right)\)は簡単に求められ，

$$S\left({r_{0}}\right)=2\pi{r_{0}} $$

これを式(5)に代入すれば，

$${E\left({r_{0}}\right)}=\frac{q}{2\pi{r_{0}}\epsilon}$$

この計算は一般の\(r\in{[a,b]}\)について成立するため，\(r_{0}\)を\(r\)に書き換えて，

$${E\left({r}\right)}=\frac{q}{2\pi{r}\epsilon} \tag{6}$$

これにより，待望の\(E\left({r}\right)\)を計算することができた．つまり下記の図4のように，電界の大きさ（グラフ内では\(\left|\vec{E}\right|\)と表記）をプロットすることができる．

 

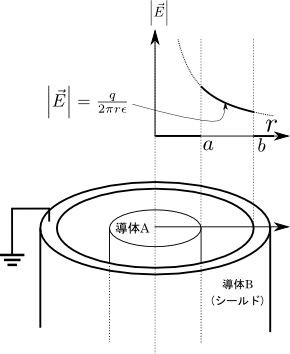
図4.ケーブルにおける電界の分布

 

 

　この電界を\(a\)から\(b\)まで積分することで導体Aと導体Bとの間の電位差\(V_{AB}\)を求めることができるというのが式(1)の意味であった．実際式(6)を式(1)に代入すると電位差\(V_{AB}\)を求めることができ，

$$\begin{eqnarray*}V_{AB} &=& \int_{a}^{b}\frac{q}{2\pi{r}\epsilon}dr &=& \frac{q}{2\pi\epsilon}\int_{a}^{b}\frac{dr}{r} &=& \frac{q}{2\pi\epsilon}\log\left(\frac{b}{a}\right) \tag{7} \end{eqnarray*}$$

式(2)に式(7)を代入すると，単位長さ当たりのケーブルの静電容量\(C\)は，

$$C = \frac{q}{\frac{q}{2\pi\epsilon}\log\left(\frac{b}{a}\right)}=\frac{2\pi\epsilon}{\log\left(\frac{b}{a}\right)} \tag{8}$$

 

 

　これにより単位長さ当たりのケーブルの静電容量を計算できた．この式に一つ典型的な値を入れてみよう．架橋ポリエチレンケーブルで\(\frac{b}{a}=1.5\)の場合に式(8)の値がどの程度になるか計算してみる．真空誘電率は\({\epsilon}_{0}=8.853\times{10^{-12}} [F/m]\)，架橋ポリエチレンの比誘電率は\(2.3\)程度なので，式(8)は以下のように計算される．

$$C =\frac{2\pi\times{2.3}{\epsilon}_{0}}{\log\left({1.5}\right)}=3.16\times{10^{-10}} [F/m] \tag{9}$$

電力用途では\(\mu{F}/km\)の単位で表すことが一般的なので，上記の式(9)を書き直すと\(0.316[\mu{F}/km]\)となる．ケーブルで用いられる絶縁材料の誘電率は大体\(2\sim3\)程度に落ち着くので，ほぼ\(\frac{b}{a}\)の値で\(C\)が決まる．そして\(\frac{b}{a}\)の値が\(1.3\sim2\)程度とすれば，比誘電率を\(2.3\)として\(C\)の値は\(0.506\sim0.193[\mu{F}/km]\)と計算される．大抵のケーブル（単心）の静電容量はこの範囲内に収まる．三心ケーブルの場合は三相それぞれがより合わさり，その相間静電容量が大きいため上記の計算をそのまま適用することはできないが，それらの静電容量の大きさも似たような値に落ち着く．

 

これでケーブルの静電容量について計算をし，その大体の大きさも把握できた．次の記事においてはケーブルのインダクタの計算を行う．

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス