理想的な変圧器と実際の変圧器

 

　前回までは，下記の図1に示すような変圧器の電気的性質について，そのイメージや物理的原理について説明してきた．それらの議論においては，一次側電圧\(V_{1}\)，一次側電流\(I_{1}\)，二次側電圧\(V_{2}\)，二次側電流\(I_{2}\)，との間に下記の関係式を満たす状況（ここではこれらの式を満たす変圧器を”理想的な”変圧器と呼ぶことにする）を考えていた．

$$V_{1}:V_{2} = N_{1}:N_{2} \tag{1}$$
$$I_{1}:I_{2} = N_{2}:N_{1} \tag{2}$$

本記事では，実際の変圧器がこの「理想的」な特性からどのように食い違うのか，理想と実際の対比を取りながら明快に説明していく．

　

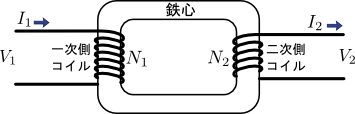
図1.２巻線変圧器（巻数比\(\frac{N_{1}}{N_{2}}\)）

 

 

　まず，図1が上記の式(1)・式(2)を満たすのは近似的な話であるということを強調しておきたい．このことを明確にするため，この図1の変圧器の二次側コイルを短絡/開放して，一次側からみた電気的性質がどうなるのか見ていきたい．まずは二次側の短絡から考えよう．

　

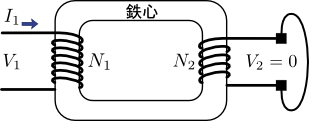
図2.変圧器の二次側を短絡

 

 

　このように二次側を短絡した場合，一次側から見て変圧器はどのように見えるだろうか．理想的な変圧器であれば常に

$$V_{1}:V_{2} = N_{1}:N_{2} $$

であり，\(V_{2}=0\)であることから\(V_{1}\)も\(0\)，つまり一次側から見ても短絡された回路として見える．しかし実際の変圧器においては一次側から覗いた電気的特性は，完全な短絡には見えない．次の図3を見て頂こう．

 

図3.二次側短絡の場合の理想的な変圧器（左）と実際の変圧器（右）

 

 

　図3の左側は理想的な変圧器の場合の等価回路，同図右側は実際の変圧器における等価回路である．理想的な変圧器であれば，二次側が短絡すれば等価的に一次側もインピーダンス\(0\)の状態になる．しかし実際には一次側や二次側のコイルには寄生抵抗があり，また漏れ磁束に起因するインダクタンス（漏れインダクタンス）も存在する．ということで現実的な変圧器においては図3の左に示すように，\(R\)や\(jX_{leak}\)が直列に入ることになる．

　ただし，必ずしもこの漏れインダクタンスが\(0\)であることが理想的かと言えば，そうでもない．なぜなら実際の電力ネットワークにおいて短絡電流が過大になることは問題であり，その短絡電流が許容範囲に収まるためには変圧器のリアクタンス成分が重要な働きをすることはよくあるからだ．また，トランスの漏れインダクタンスを積極的に用いた調相設備もある．以上のことから漏れインダクタンスがないということを”理想的”と呼ぶのは少し安直かもしれない．しかしここではこのような実際的な話は置いておいて，あくまで理論的に変圧器の機能だけを達成する変圧器を”理想的”と呼んで話を続けていく．次に，変圧器の二次側を開放した例を次の図4に示す．

 

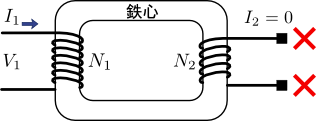
図4.変圧器の二次側を開放

 

 

　図4のように二次側を開放にすると，\(I_{2}=0\)となるので，下記の理想的な変圧器が満たす式

$$I_{1}:I_{2} = N_{2}:N_{1} $$

を思い出せば，\(I_{1}=0\)となる．つまり，二次側から見ても，断線しているように見えるのである．しかし実際には二次側を開放端にしたからと言って，全く一次側に電流が流れないわけではない．わずかに励磁電流が流れるのである．下の図5にてまとめよう．

 

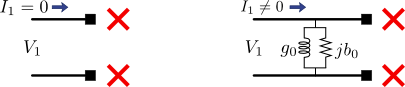
図5.二次側開放の場合の理想的な変圧器（左）と実際の変圧器（右）

 

 

　励磁電流が全く流れず，二次側が開放ならば一次側も開放になるのが理想的な変圧器（図5の左側）であり，二次側が開放であってもわずかながら励磁電流が流れるというのが実際の変圧器（図5の右側）である．

　続いて図6に示すように，変圧器の二次側にインピーダンス\(Z_{2}\)を接続した場合を考える．

 

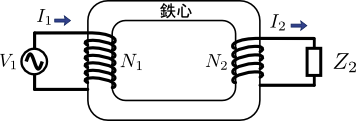
図6.二次側にインピーダンス\(Z_{2}\)を接続したとき

 

 

　この図6の状況では，変圧器は一次側から見てどのような電気的特性を持つだろうか？結論から言えば，二次側につないだインピーダンス\(Z_{2}\)は，一次側から見ると巻数比\(\frac{N_{1}}{N_{2}}\)の２乗倍されたように見える．等価的には図7の左側の通りである．

 

図7.二次側にインピーダンス\(Z_{2}\)を接続したときの理想的な変圧器（左）と実際の変圧器（右）

 

 

　一方で実際の変圧器については図7の右側に示す通り，一次側換算インピーダンス\(\left(\frac{N_{1}}{N_{2}}\right)^{2}Z_{2}\)に漏れインダクタンス\(jX_{leak}\)や一次換算抵抗\(R\)，励磁電流を表すコンダクタンス\(g_{0}\)やサセプタンス\(jb_{0}\)が加わった形に見える．これは実際の変圧器の等価回路である．計算なども含めたこれらの詳しい議論は後半の記事や著書などで述べることになるだろう．

　次の記事では，この理想的な変圧器を題材にして，PU法を導入していくことにしよう．

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス