変圧器のPU法(実践編)

 

　前回の記事において，理想的な変圧器にPU法を当てはめると変圧器が単なる導線として扱えることを示した．本記事ではその議論をベースにして，変圧器にPU法を適用しつつ漏れインダクタンスなどの理想的でない効果を組み込む方法や，電力系統では極めて一般的な3巻線変圧器の扱い方などを説明していく．

 

 

実際の変圧器へのPU法適用

 

　理想的でない変圧器は，以前の記事”理想的な変圧器と実際の変圧器”に示した通り，漏れインダクタンスや寄生抵抗，励磁電流などが存在する．電力系統安定性や短絡電流の解析など，多くのケースにおいて励磁電流の効果は無視できるが，寄生抵抗や漏れインダクタンス，特に漏れインダクタンスの効果は必ずと言っていいほど考慮しなければならない．そこで，寄生抵抗と漏れインダクタンスを無視しないで変圧器にPU法を適用してみるとどうなるのか，次の図1に示してみた．

 

図1.理想的でない変圧器（実際の変圧器）にPU法を適用

 

 

　PU法を適用したので，今までの議論でも明らかな通り，変圧器（の理想的な部分）は導線となる．今回はその導線に寄生抵抗と漏れインダクタンス（理想的でない成分）が直列に挿入される形（図6の右側）として等価回路が表現される．そして，寄生抵抗\(\overline{R} [p.u.]\)とリアクタンス\(j\overline{X} [p.u.]\)はすでにPU値なので，「一次側から見たときは，，，」とか，「二次側換算は，，，」等といった変換は一切不要である．変圧器自身はほぼ導線となって一次側と二次側の区別が無くなり，そこにわずかな寄生抵抗と漏れインダクタンスが付いてくるのである．ここで\(p.u.\)値で表された寄生抵抗と漏れインダクタンスについて，適当な値を入れて少し具体的な議論をしてみよう．

$$\overline{R}=0.01 [p.u.] \tag{1}$$
$$\overline{X}=0.05 [p.u.]\tag{2}$$

としてみる．すると，インピーダンスのPU値\(\overline{Z}\)は，

$$\overline{Z}=0.01+j0.05 [p.u.]$$

となる．この物理的な意味を言葉にすると，「定格電流が流れているとき，変圧器の前後の電位差の抵抗成分（電流と同位相の成分）は定格電圧の\(0.01\)倍，誘導成分（電流から\(90^{\circ}\)進んだ成分）は定格電圧の\(0.05\)倍の大きさを持つ．」となる．また，多くの変圧器の漏れインダクタンスや寄生抵抗の\(p.u.\)値は百分率で表した方が見やすい．上記の例ならば

$$\%Z=1+j5 [\%]$$

という風に表される．このように理想的でない現実の変圧器についてもPU法を当てはめることができ，また寄生抵抗や漏れインダクタンスなどはその導線に対して直列に挿入され，\(p.u.\)値ないしは\(\%\)値で表される．

　これまでは２巻線変圧器に絞って話を進めてきたが，実際の送電用変圧器の多くは３巻線形となっている．それは所内電源を確保したり調相設備を接続する際に三次巻線を用いると便利だからである．という訳で，３巻線変圧器にもPU法を適用してみよう．

 

３巻線変圧器へのPU法適用

 

　まず３巻線変圧器の模式図を下記に示そう．

 

図2.３巻線変圧器の模式図

 

 

　２巻線変圧器のときと同様に，それぞれのコイルの電圧・電流が満たす関係を導いていきたい．その際に電流の符号は２巻線のときとは異なり，３つの巻線の３つの電流がそれぞれ同じ向きで正とする．つまり，「\(I_{1}\)が正のとき」「\(I_{2}\)が正のとき」「\(I_{3}\)が正のとき」とで生じる磁束の向きはそれぞれ同じであるとする．また，鉄心の磁束は\(\Phi\)とし，３つのコイルに漏れなくこの磁束が貫くものとする（漏れ磁束を無視）．

　まず３つの電圧についての関係を導く．ファラデーの法則から

$$V_{1} = N_{1}\frac{d\Phi}{dt} \tag{3}$$
$$V_{2} = N_{2}\frac{d\Phi}{dt} \tag{4}$$
$$V_{3} = N_{3}\frac{d\Phi}{dt} \tag{5}$$

が成立する．そして\(\frac{d\Phi}{dt}\)は共通であることから

$$V_{1}:V_{2}:V_{3} = N_{1}:N_{2}:N_{3} \tag{6}$$

という関係を満たす．また2巻線のときの議論にもあった通り，鉄心の透磁率が非常に高く，わずかな起磁力でも大きな磁束を発生させるため，図2の鉄心に働く起磁力

$$ N_{1}I_{1}+N_{2}I_{2}+N_{3}I_{3} \tag{7}$$

は非常に小さくて済む．つまり近似的には

$$ N_{1}I_{1}+N_{2}I_{2}+N_{3}I_{3}=0 \tag{8}$$

が成立すると考えてよい．これら式(6)と式(8)こそ理想的な3巻線変圧器が満たす関係である．一方で，それらに対する基準電圧（\(V_{base1}, V_{base2}, V_{base3}\)）が満たすべき関係も同じく，

$$V_{base1}:V_{base2}:V_{base3} = N_{1}:N_{2}:N_{3} \tag{9}$$

となる．ここで基準皮相電力が３巻線間で等しいとすると（同一変圧器の各巻線間では電力基準値を必ず合わせる），

$$V_{base1}I_{base1}=V_{base2}I_{base2}=V_{base3}I_{base3} \tag{10}$$

が成立するため，基準電流（\(I_{base1}, I_{base2}, I_{base3}\)）が満たすべき関係は式(9)と逆数の関係になり

$$I_{base1}:I_{base2}:I_{base3} = \frac{1}{N_{1}}:\frac{1}{N_{2}}:\frac{1}{N_{3}} \tag{11}$$

となるだろう．

　式(6)と式(9)から明らかに

$$ \frac{V_{1}}{V_{base1}}=\frac{V_{2}}{V_{base2}}=\frac{V_{3}}{V_{base3}} \tag{12}$$

が成り立つ．また，式(8)と式(11)から

$$ \frac{I_{1}}{I_{base1}}+\frac{I_{2}}{I_{base2}}+\frac{I_{3}}{I_{base3}}=0 \tag{13}$$

が成立することも簡単に証明できる．すなわち，PU法の定義を

$$ \overline{V_{1}}=\frac{V_{1}}{V_{base1}}, \overline{V_{2}}=\frac{V_{2}}{V_{base2}}, \overline{V_{3}}=\frac{V_{3}}{V_{base3}} \tag{14}$$
$$ \overline{I_{1}}=\frac{I_{1}}{I_{base1}}, \overline{I_{2}}=\frac{I_{2}}{I_{base2}}, \overline{I_{3}}=\frac{I_{3}}{I_{base3}} \tag{15}$$

とすれば，式(12)と式(13)は

$$ \overline{V_{1}}=\overline{V_{2}}=\overline{V_{3}} \tag{16}$$
$$ \overline{I_{1}}+\overline{I_{2}}+\overline{I_{3}}=0 \tag{17}$$

となる．これがPU法を適用したあとの3巻線変圧器が満たす電圧・電流の関係である．この結果を視覚的に表すと次の図3のようになる．

 

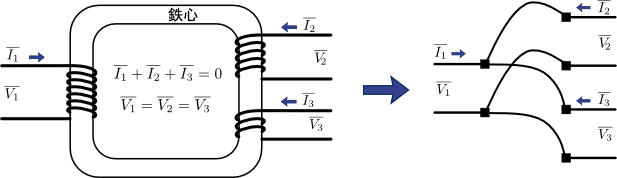
図3.３巻線変圧器にPU法を適用

 

 

　まず，式(16)からPU法を適用すれば３つの巻線の起電力がすべて等しくなり，また式(17)から電流の総和が\(0\)であるというキルヒホッフの法則が成り立っている．したがってPU法を適用したあとの3巻線変圧器は図3の右側のような形に置き換えることができるのである．2巻線変圧器が単なる導線だったのに対し，3巻線変圧器はT字分岐の導線としてとらえることができるのだ．変圧器のPU法に関するイメージがだいぶ湧いただろうか？この詳しい議論などは書籍等に掲載予定である．

 

 

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス