対称座標法を用いた短絡電流の計算

 

　本記事では実際に対称座標法を用いて，短絡や地絡事故時における事故電流が簡単に求められるということを示していこう．対称座標法が何かということは既知のものとして説明を進めるので，もし下記の説明で分からない部分があれば，適宜前回の記事などで対称座標法の復習をしていただきたい．

 

 

対称座標法を用いた三相地絡電流の計算

 

　対称座標法を用いれば，例えば下記のような三相地絡事故時の地絡電流も簡単に求めることができることを示そう．

　

 

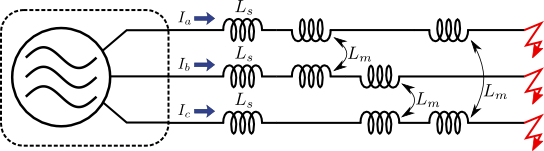
図1.三相地絡事故

 

 

　送電線は相互インダクタンスもあり計算が大変そうに見えるが，ここで対称座標法を用いれば図2に示すように大変シンプルな回路に変換することができる．

 

 

図2.図1に対称座標法を適用した場合

 

 

　対称座標法を用いると，相互インダクタンスを含む複雑なインダクタンス系は独立な3本のインダクタンスへとほどくことができる．また三相地絡の事故点は，対称座標法を適用した後も三相地絡のままである．なぜなら，三相地絡を意味する

$$ \begin{pmatrix} V_{a}\\ V_{b}\\ V_{c} \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \tag{1} $$

は，対称座標法を用いても

$$ \begin{pmatrix} V_{0}\\ V_{1}\\ V_{2} \end{pmatrix}= \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \tag{2} $$

と表すことができ，依然として零相(0相)・正相(1相)・逆相(2相)の3本が電圧\(0\)になっている（つまり三相地絡している）といえるからだ．そしてここでは簡単のため，発電機のインピーダンスは\(0\)であるとし，正相(1相)電圧\(V_{1}\)のみ\(0\)ではなく，零相(0相)と逆相(2相)はともに\(0V\)であるとした．この場合，地絡電流は非常に簡単に求めることができ，

$$ \begin{pmatrix} I_{0}\\ I_{1}\\ I_{2} \end{pmatrix}= \begin{pmatrix} 0\\ \frac{V_{1}}{j\omega\left(L_{s}-L_{m}\right)}\\ 0 \end{pmatrix} \tag{3} $$

となる．図2を見れば明らかなように，\(I_{0}=I_{2}=0\)であり，かつ\(I_{1}\)はインダクタンス\(L_{s}-L_{m}\)に電圧\(V_{1}\)をかけたときの電流値に等しいため，上記の式(3)のように求まるのである．ここで元々の図1におけるa相・b相・c相の地絡電流値が欲しければ，上記の式(3)に\(\boldsymbol{a}^{-1}\)をかけて逆変換してやればよい．

$$ \begin{pmatrix} I_{a}\\ I_{b}\\ I_{c} \end{pmatrix}= \boldsymbol{a}^{-1} \begin{pmatrix} 0\\ \frac{V_{1}}{j\omega\left(L_{s}-L_{m}\right)}\\ 0 \end{pmatrix}=j\omega\left(L_{s}-L_{m}\right)\begin{pmatrix} 1\\ a^{2}\\ a \end{pmatrix} \tag{4} $$

ただし，\(a\)は複素数で

$$a = \frac{-1+j\sqrt{3}}{2} \tag{5}$$

 

　ここまで簡単な問題になってしまうのである．上記の図2への変換がどうして成り立つのかわからない場合は，前回の記事にて対称座標法の復習をしていただきたい．それでは次に，きっちり発電機のインピーダンスも考慮した場合を解いてみよう．

 

 

図3.図2に発電機のインピーダンスを加えた場合

 

 

　発電機の零相インピーダンスを\(L_{G0}\)，正相インピーダンスを\(L_{G1}\)，逆相インピーダンスを\(L_{G2}\)とすると図2は図3のようになる．そして発電機の起電力が正相成分のみであるとすれば，零相電流\(I_{0}\)や逆相電流\(I_{2}\)は流れようがなく，やはり\(I_{0}=I_{2}=0\)であることは変わりない．そして正相インピーダンスは\(L_{s}-L_{m}\)に\(L_{G1}\)が加わっただけであり，地絡電流は

$$ \begin{pmatrix} I_{0}\\ I_{1}\\ I_{2} \end{pmatrix}= \begin{pmatrix} 0\\ \frac{V_{1}}{j\omega\left(L_{G1}+L_{s}-L_{m}\right)}\\ 0 \end{pmatrix} \tag{6} $$

と，式(3)に\(L_{G1}\)が加わっただけの形であっさり解ける．これをa相・b相・c相の地絡電流値にしたければ，先ほどと同様に\(\boldsymbol{a}^{-1}\)を掛けてあげて

$$ \begin{pmatrix} I_{a}\\ I_{b}\\ I_{c} \end{pmatrix}= \boldsymbol{a}^{-1} \begin{pmatrix} 0\\ \frac{V_{1}}{j\omega\left(L_{G1}+L_{s}-L_{m}\right)}\\ 0 \end{pmatrix}=j\omega\left(L_{G1}+L_{s}-L_{m}\right)\begin{pmatrix} 1\\ a^{2}\\ a \end{pmatrix} \tag{7} $$

と求まる．発電機のインピーダンスも零相(0相)・正相(1相)・逆相(2相)のそれぞれが独立しているため，やはりあっさりと解ける．もう少し理解を深めるため，今度は三相地絡ではなく三相短絡であった場合の事故電流を求めることにしよう．

 

 

対称座標法を用いた三相短絡電流の計算

 

　今度は下記のような三相短絡事故において，短絡電流がどうなるのか計算してみよう．

　

 

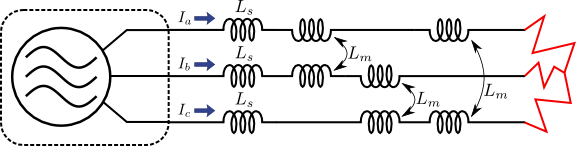
図4.三相短絡事故

 

 

　このケースにおいても対称座標法が有効であることは言うまでもない．早速図4に対称座標法を適用してみよう．

 

 

図5.図4に対称座標法を適用した場合

 

 

　今度は初めから発電機のインピーダンスを考慮して計算しよう．発電機のインピーダンスは前回の計算同様，零相について\(L_{G0}\)，正相\(L_{G1}\)，逆相\(L_{G2}\)とする．また，送電線のインダクタンスも前回同様，3本の独立なインダクタンスに変換される．また三相短絡の場合，対称座標法を適用した後は零相のみ開放となる点が三相地絡のときと異なる点である．なぜなら，三相短絡の場合

$$ I_{a}+I_{b}+I_{c}=0 \tag{8} $$

を満たすが，これは零相電流の3倍である\(3I_{0}\)であり，すなわち

$$ I_{0}=0 \tag{9} $$

となるため，図5に示すように，今度は零相だけ事故点は開放端として表されるのである．ただし，この図5は図3と全く同じ事故電流が流れることは明らかである．なぜなら\(I_{0}=I_{2}=0\)であることは変わりなく，また零相成分の違いだけで正相成分については全く同じ回路になっているからである．よって，求める短絡電流は

$$ \begin{pmatrix} I_{0}\\ I_{1}\\ I_{2} \end{pmatrix}= \begin{pmatrix} 0\\ \frac{V_{1}}{j\omega\left(L_{G1}+L_{s}-L_{m}\right)}\\ 0 \end{pmatrix} \tag{10} $$

となり，これをa相・b相・c相の地絡電流値にしたければ，先ほどと同様に\(\boldsymbol{a}^{-1}\)を掛けてあげて

$$ \begin{pmatrix} I_{a}\\ I_{b}\\ I_{c} \end{pmatrix}= \boldsymbol{a}^{-1} \begin{pmatrix} 0\\ \frac{V_{1}}{j\omega\left(L_{G1}+L_{s}-L_{m}\right)}\\ 0 \end{pmatrix}=j\omega\left(L_{G1}+L_{s}-L_{m}\right)\begin{pmatrix} 1\\ a^{2}\\ a \end{pmatrix} \tag{11} $$

となる．やはり大変シンプルな問題に帰着できた．このケースでは正相成分のみ起電力を持っているケースだったため三相短絡と三相地絡は全く同じ事故電流となった．零相電圧が\(0\)ではない場合に初めて，両者の結果に差が生まれる．

　同様にして1線地絡，2線地絡，2線短絡などの事故電流も対称座標法を用いれば簡単に解くことができるが，この辺りは書籍にて詳しく議論することにしよう．

 

News!! ☆2015年10月5日より、EnergyChordの新刊【[改訂版]徹底解説 電動機・発電機の理論】の発売を開始しました！
          ☆【入門演習 パワーエレクトロニクス】も好評発売中です！試読はこちらから。

"Energy"コンテンツトップに戻る

徹底解説 電動機・発電機の理論 入門演習パワーエレクトロニクス 応用演習パワーエレクトロニクス