フーリエ級数展開まとめ

 

 

　前々回の記事，”フーリエ級数展開はなぜ成り立つのか”からも，「ほとんどすべての関数は，サイン波の足し合わせで表現できる」ということが理解できたことと思う．特に，下記の図1のような周期関数の場合には，その基本周期に等しいサイン波とその整数倍の周波数（または波数）のサイン波とを無限に足し合わせた級数として表すことができるのである．

 

 

 

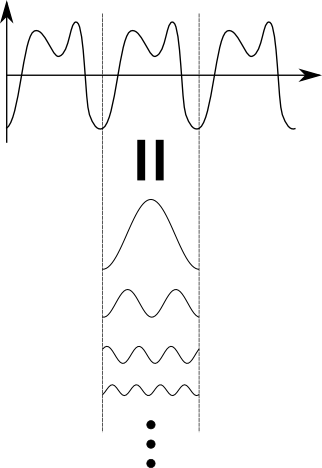
図1.フーリエ級数展開のイメージ

 

 

　具体的に式で表してみよう．”フーリエ級数展開はなぜ成り立つのか”の終盤でも説明しているが，任意の連続な

関数\(f\left({x}\right)\left({0}\leq{x}\leq{L}\right)\)は，次のようにサイン・コサイン関数の級数として展開できる．

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{\infty}\left[a_{n}\cos\left(\frac{2n\pi}{L}x\right)+b_{n}\sin\left(\frac{2n\pi}{L}x\right)\right] \tag{1}$$

 

　上記式(1)の\(\Sigma\)内の\(\sin{,}\cos\)はすべて，\(x\)軸に対して\(L\)だけ平行移動しても値は変わらないので，式(1)自体が基本周期\(L\)の周期関数になっている．つまり，関数\(f\left({x}\right)\left({0}\leq{x}\leq{L}\right)\)が，\(x\geq{L}\)においても周期\(L\)で繰り返される形となる．このように，ある区間で連続な任意の関数は，その区間においてサイン波の重ね合わせとして級数展開でき，これをフーリエ級数展開と呼んでいる．

　具体的に，上記の式(1)で表したフーリエ級数展開の式をグラフにしてみると次の図2のようになる．

 

 

 

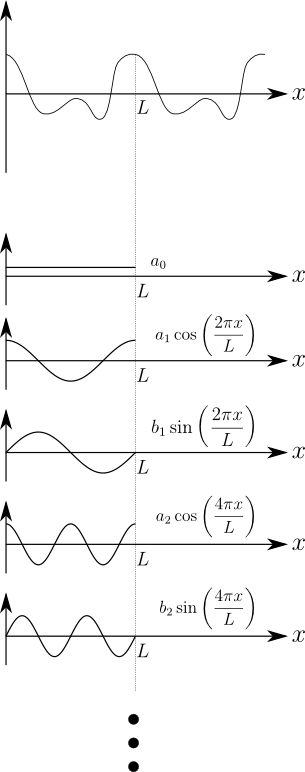
図2.フーリエ級数展開の式(1)のイメージ

 

 

　式(1)のイメージは図2に示す通り，基本周期\(L\)の周期関数を表現するため，まずはこの周期関数の平均値\(a_{0}\)を求め，そこへ同じく周期\(L\)の正弦波である

$$\cos{\frac{2\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\pi{x}}{L}}$$

をそれぞれ\(a_{1}\)倍，\(b_{1}\)倍して加え，そこへその倍波の正弦波である

$$\cos{\frac{4\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{4\pi{x}}{L}}$$

をそれぞれ\(a_{2}\)倍，\(b_{2}\)倍して加え，

$$\cdot\cdot\cdot$$

といった具合に，際限なく高次の高調波までを，その振幅を調整しながら足し合わせ続けることで，元々表現しようとしていた\(f\left({x}\right)\)に漸近していくというものである．とにかく，余程酷い関数（不連続点が無限個あるなど）でない限り，上記の式(1)のように級数展開できることは理解したとしよう．では，これらの正弦波の係数\(a_{n},\,{b}_{n}\)はどのように求めるのだろうか？実は次の3つの関係式を使うことで，非常に簡単に\(a_{n}\)や\(b_{n}\)を求めることができるのである．

$$ \int_{0}^{2\pi}{\cos{mx}\cos{nx}} = \left\{\begin{matrix} 0\,\,(m\neq{n})\\ \pi\,\,(m={n}) \end{matrix}\right. \tag{2} $$
$$ \int_{0}^{2\pi}{\cos{mx}\sin{nx}} =0 \tag{3}$$
$$ \int_{0}^{2\pi}{\sin{mx}\sin{nx}} = \left\{\begin{matrix} 0\,\,(m\neq{n})\\ \pi\,\,(m={n}) \end{matrix}\right. \tag{4} $$

ただし\(m\)も\(n\)も自然数とする．関数論的にはこれは関数の直交性を表しているのだが，その辺りの説明は一旦おいとくとして，この式(2)～(4)がなぜ係数\(a_{n},\,{b}_{n}\)の算出に役立つのか，その計算を実際に見てみることにしよう．話を見えやすくするため，まずは式(1)の関数\(f\left({x}\right)\)の周期\(L\)を\(2\pi\)としてみる．すると式(1)は

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{\infty}\left[a_{n}\cos{nx}+b_{n}\sin{nx}\right] \tag{5}$$

となる．この式(5)に\(\cos{kx}\)（\(k\geq{1}\)）を掛けて\({0}\sim{2\pi}\)の区間で積分してやれば，式(2)～(4)を用いることで

$$\int_{0}^{2\pi}\cos{kx}f\left({x}\right)dx=\pi{a}_{k} \tag{6}$$

と，非常に簡単にできてしまうのである！しかも\(a_{k}\)がほとんど求まっている．何が起きたのか，もうちょっと詳しく見てみよう．式(5)は次の式(7)に示すように(i)定数項，(ii)\(\cos\)級数，(iii)\(\sin\)級数，の３つの部分に分けられる．

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{\infty}a_{n}\cos{nx}+\sum_{n=1}^{\infty}b_{n}\sin{nx} \tag{7}$$

これに\(\cos{kx}\)を掛けて\({0}\sim{2\pi}\)の区間で積分するので

 

$$\int_{0}^{2\pi}\cos{kx}f\left({x}\right)dx=\int_{0}^{2\pi}a_{0}\cos{kx}dx+\int_{0}^{2\pi}\cos{kx}\left[\sum_{n=1}^{\infty}a_{n}\cos{nx}\right]dx\\+\int_{0}^{2\pi}\cos{kx}\left[\sum_{n=1}^{\infty}b_{n}\sin{nx}\right]dx$$

右辺第１項は\(\cos\)関数の\(k\)周期平均なので当然\(0\)となる．また右辺第3項は\(\sin\)と\(\cos\)の積の積分なので，式(3)によりこれも\(0\)となる．よって上記の式は

$$\int_{0}^{2\pi}\cos{kx}f\left({x}\right)dx=\int_{0}^{2\pi}\cos{kx}\left[\sum_{n=1}^{\infty}a_{n}\cos{nx}\right]dx \tag{8}$$

というところまで単純化できる．またこの計算は式(2)を使えば

$$\int_{0}^{2\pi}\cos{kx}\left[\sum_{n=1}^{\infty}a_{n}\cos{nx}\right]dx=\sum_{n=1}^{\infty}a_{n}\int_{0}^{2\pi}\cos{kx}\cos{nx}dx=\pi{a}_{k} \tag{9}$$

とできる．式(2)によれば，式(9)の第２式の\(n\)と\(k\)が等しいときだけ積分が\(0\)でなくなるためである．式(8)と式(9)により，式(6)が確かに説明できた．同様にして式(5)に\(\sin{kx}\)（\(k\geq{1}\)）を掛けて\({0}\sim{2\pi}\)の区間で積分してやれば，式(2)～(4)を用いることで

$$\int_{0}^{2\pi}\sin{kx}f\left({x}\right)dx=\pi{b}_{k} \tag{10}$$

と計算できるのである．式(6)や式(10)を\(a_{k}\)や\(b_{k}\)について整理すれば，

$$a_{k}=\frac{1}{\pi}\int_{0}^{2\pi}\cos{kx}f\left({x}\right)dx \tag{11}$$
$$b_{k}=\frac{1}{\pi}\int_{0}^{2\pi}\sin{kx}f\left({x}\right)dx \tag{12}$$

（ただし，\(k\geq{1}\)）このように，\(f\left({x}\right)\)に\(\sin\)や\(\cos\)を掛けたものの積分で\(a_{k}\)や\(b_{k}\)が求まることがわかった．今までの議論は\(f\left({x}\right)\)の周期\(L\)が\(2\pi\)での話であったが，そもそもの式(1)の \(a_{k}\)や\(b_{k}\)はどうやって求めるのか？

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{\infty}\left[a_{n}\cos\left(\frac{2n\pi}{L}x\right)+b_{n}\sin\left(\frac{2n\pi}{L}x\right)\right] \tag{1}$$

単に\(x\)軸に対して伸縮しただけであるから，\(a_{k}\)や\(b_{k}\)の求め方は当然同じである！\(\cos\left(\frac{2k\pi}{L}x\right)\)や\(\sin\left(\frac{2k\pi}{L}x\right)\)を掛けて，1周期\([0,\,{L}]\)について積分してやればよいのである．すると\(k\geq{1}\)について

$$a_{k}=\frac{2}{L}\int_{0}^{L}\cos\left(\frac{2n\pi}{L}x\right)f\left({x}\right)dx \tag{13}$$
$$b_{k}=\frac{2}{L}\int_{0}^{L}\sin\left(\frac{2n\pi}{L}x\right)f\left({x}\right)dx \tag{14}$$

と計算できる．これは式(2)～(4)を\(x\rightarrow{\frac{2\pi{x}}{L}}\)と変数変換したものである以下の３式を用いれば証明できる．

$$ \int_{0}^{L}{\cos\left(\frac{2m\pi}{L}x\right)\cos\left(\frac{2n\pi}{L}x\right)} = \left\{\begin{matrix} 0\,\,(m\neq{n})\\ \frac{L}{2}\,\,(m={n}) \end{matrix}\right. \tag{2'} $$
$$ \int_{0}^{L}{\cos\left(\frac{2m\pi}{L}x\right)\sin\left(\frac{2n\pi}{L}x\right)} =0 \tag{3'}$$
$$ \int_{0}^{L}{\sin\left(\frac{2m\pi}{L}x\right)\sin\left(\frac{2n\pi}{L}x\right)} = \left\{\begin{matrix} 0\,\,(m\neq{n})\\ \frac{L}{2}\,\,(m={n}) \end{matrix}\right. \tag{4'} $$

波形が\(x\)軸に対して伸縮しても上記の性質が保存されることは明らかであろう．ただし，積分結果は伸縮した倍率に比例して異なる．また，\(a_{0}\)はまだ求まっていない．\(k\geq{1}\)であったからである．しかし\(a_{0}\)は一番簡単に求まる．\(a_{0}\)は式(1)の関数の１周期平均に他ならない．

$$a_{0}=\frac{1}{L}\int_{0}^{L}f\left({x}\right)dx \tag{15}$$

 

これにて式(1)の係数である\(a_{0}\)，\(a_{k}\)，\(b_{k}\)（\(k\geq{1}\)）の全てを式(13)～(15)により求めることができるようになった！ここで２つ課題を提供したい．図3と図4のフーリエ級数展開を，式(1)，式 (13)～(15)を用いて実行してほしい．

 

 

 

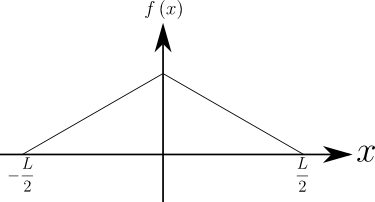
図3.偶関数の例

 

 

 

 

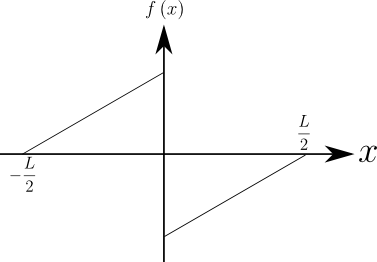
図4.奇関数の例

 

 

　詳しい計算はここでは紹介しないが，勘所だけ伝えよう．まず，図3は偶関数であるから\(\cos\)だけで構成される級数となり，\(\sin\)の係数である\(b_{k}\)はすべて\(0\)になる．逆に図4は奇関数であるから\(\sin\)だけで構成される級数となり，\(\cos\)の係数である\(a_{k}\)はすべて\(0\)になる．また，式(13)～(15)は積分範囲\([0,\,{L}]\)であったが，図3図4ともに\([-\frac{L}{2},\,\frac{L}{2}]\)で定義されている．「これは式(13)～(15)を用いて計算できないのではないか？」と思われたかもしれないが全く問題ない．なぜなら積分範囲の幅が\(L\)でありさえすれば，常に式(2')～(4')は成り立つからである．つまり式(2')～(4')の直交性の式は次のように拡張できる：

$$ \int_{-\alpha}^{L-\alpha}{\cos\left(\frac{2m\pi}{L}x\right)\cos\left(\frac{2n\pi}{L}x\right)} = \left\{\begin{matrix} 0\,\,(m\neq{n})\\ \frac{L}{2}\,\,(m={n}) \end{matrix}\right. \tag{2"} $$
$$ \int_{-\alpha}^{L-\alpha}{\cos\left(\frac{2m\pi}{L}x\right)\sin\left(\frac{2n\pi}{L}x\right)} =0 \tag{3"}$$
$$ \int_{-\alpha}^{L-\alpha}{\sin\left(\frac{2m\pi}{L}x\right)\sin\left(\frac{2n\pi}{L}x\right)} = \left\{\begin{matrix} 0\,\,(m\neq{n})\\ \frac{L}{2}\,\,(m={n}) \end{matrix}\right. \tag{4"} $$

積分区間を\(\alpha\)だけ平行移動しても積分の結果は変わらない．被積分関数は\(x\)について\(L\)足せば同じ値を取るため，積分区間の幅が\(L\)であればどこをとっても積分の結果は等しいのである．このことを用いれば式(13)~(15)も次のように拡張できる：

$$a_{k}=\frac{2}{L}\int_{-\alpha}^{-\alpha+L}\cos\left(\frac{2n\pi}{L}x\right)f\left({x}\right)dx \tag{13'}$$
$$b_{k}=\frac{2}{L}\int_{-\alpha}^{-\alpha+L}\sin\left(\frac{2n\pi}{L}x\right)f\left({x}\right)dx \tag{14'}$$
$$a_{0}=\frac{1}{L}\int_{-\alpha}^{-\alpha+L}f\left({x}\right)dx \tag{15'}$$

これらの式の\(f\left({x}\right)\)に図3や図4の関数を入れて計算してやれば，図3や図4についてのフーリエ級数展開を得ることができるのだ．次の記事では，このフーリエ級数展開を無限周期の関数（周期的でなく，定義される範囲が無限の幅を持っている関数）にも適用できるように拡張したフーリエ変換について紹介していこう．