離散フーリエ変換入門
本記事では離散フーリエ変換とは何なのか,その数学的イメージを紹介していこう.
コンピュータで行われるフーリエ変換は基本的に離散フーリエ変換である.なぜなら,電子計算機は連続量をそのまま扱うことができないため,コンピュータが処理するデータは必ず離散化される必要があるからである.つまり,コンピュータによるデータ処理が当たり前となった現代技術においては,フーリエ変換と言えば離散フーリエ変換を指すと言っても過言ではない.
一方でフーリエ変換の教科書における離散フーリエ変換の扱いはどうだろうか?未だに多くの教科書は,離散フーリエ変換を最後あたりに少し載せる程度にとどまっているというのが現状なのではないだろうか?ここでは,離散フーリエ変換は決して特殊でもマニアックなものでもなく,むしろ非常にシンプルなものであり,かつフーリエ変換全般の理解を強力に助けるものであることを体感していただこう.
まず,下記の図1に示すように離散化されたデータについて離散フーリエ変換することを考えてみよう.
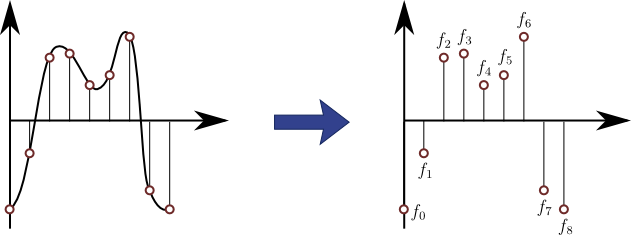
図1.連続量を横軸に関して離散化
離散フーリエ変換の基本的なイメージとしては,とにかく図1のような離散的な点をすべて通るようなサイン・コサインの重ね合わせを割り出すというところにある.つまり,図1のデータの1周期を\(1\)だとすると,
$$x\left({t}\right)=a_{0}+\sum_{n=1}^{3}\left[a_{n}\cos\left(2n\pi{t}\right)+b_{n}\sin\left(2n\pi{t}\right)\right]+a_{4}\cos\left(8\pi{t}\right) \tag{1}$$
の\(8\)つの係数である\(a_{0}\sim{a}_{4}\),\(b_{1}\sim{b}_{3}\)をうまく調整してやれば,上記の\(x\left({t}\right)\)が図1の\(8\)つの値\(x_{0}\sim{x}_{7}\)を通るようにすることができる.離散フーリエ変換は,これら\(8\)つの係数を求めることと数学的には等価なのだが,実際の離散フーリエ変換では,次のように\(\cos{,}\sin\)を複素指数関数の\(e^{i\theta}\)という形の関数
$$x\left({t}\right)=\sum_{n=0}^{7}f_{n}e^{2n\pi{it}}\tag{2}$$
を使う.そしてこの関数\(x\left({t}\right)\)が図1の\(8\)つの値\(x_{0}\sim{x}_{7}\)を通るための\(8\)つの係数\(f_{0}\sim{f}_{7}\)を求めることこそが,離散フーリエ変換である.離散フーリエ変換は式(2)のような複素形式をとるため,離散フーリエ変換前の離散データ\(x_{0}\sim{x}_{7}\)は複素列であってもよく(もちろん実数列であってもよい),また変換後の離散データ\(f_{0}\sim{f}_{7}\)は一般に複素列である.(変換後の\(f_{0}\sim{f}_{7}\)が実数になるのは,\(x_{0}\sim{x}_{7}\)が偶関数の離散化データのときであり,信号処理工学の上ではこのような離散フーリエ変換を離散コサイン変換と呼んで専用のアルゴリズムを使用する.)
式(2)の関数\(x\left({t}\right)\)が図1の\(8\)つの値\(x_{0}\sim{x}_{7}\)を通るという条件を数式にすると,次のようになる.
$$x\left({0}\right)=x_{0}{,}\,\,{x}\left({\frac{1}{8}}\right)=x_{1}{,}\,\,{x}\left({\frac{2}{8}}\right)=x_{2}{,}\cdot\cdot\cdot{,}\,\,{x}\left({\frac{7}{8}}\right)=x_{7}\tag{3}$$
この\(8\)本の連立方程式を解くことで,\(8\)つの複素数である\(f_{0}\sim{f}_{7}\)を求めることができる.これは気が遠くなるような話に感じるが,実はこの連立方程式はとてもシンプルに解決する.上記の連立方程式のうち\(x_{k}\)に関する式を抜き出すと,
$$x_{k}={x}\left({\frac{k}{8}}\right)=\sum_{n=0}^{7}f_{n}e^{2n\pi{i}{\frac{k}{8}}}\tag{4}$$
となるが,ここで式(4)右辺の指数部分は,\(\omega=e^{\frac{2\pi{i}}{8}}\)が基本単位になっていることがわかる.\(\omega\)を用いて式(4)を書き直すと,
$$\sum_{n=0}^{7}\omega^{nk}f_{n}=x_{k}\tag{5}$$
つまり,\(\omega\)という複素数(ここでは\(8\)乗根)を用いた,次の複素連立方程式を解くことになる.
$$\omega^{0}f_{0}+\omega^{0}f_{1}+\omega^{0}f_{2}+\omega^{0}f_{3}+\omega^{0}f_{4}+\omega^{0}f_{5}+\omega^{0}f_{6}+\omega^{0}f_{7}=x_{0}$$
$$\omega^{0}f_{0}+\omega^{1}f_{1}+\omega^{2}f_{2}+\omega^{3}f_{3}+\omega^{4}f_{4}+\omega^{5}f_{5}+\omega^{6}f_{6}+\omega^{7}f_{7}=x_{1}$$
$$\omega^{0}f_{0}+\omega^{2}f_{1}+\omega^{4}f_{2}+\omega^{6}f_{3}+\omega^{8}f_{4}+\omega^{10}f_{5}+\omega^{12}f_{6}+\omega^{14}f_{7}=x_{2}$$
$$\omega^{0}f_{0}+\omega^{3}f_{1}+\omega^{6}f_{2}+\omega^{9}f_{3}+\omega^{12}f_{4}+\omega^{15}f_{5}+\omega^{18}f_{6}+\omega^{21}f_{7}=x_{3}$$
$$\omega^{0}f_{0}+\omega^{4}f_{1}+\omega^{8}f_{2}+\omega^{12}f_{3}+\omega^{16}f_{4}+\omega^{20}f_{5}+\omega^{24}f_{6}+\omega^{28}f_{7}=x_{4}$$
$$\omega^{0}f_{0}+\omega^{5}f_{1}+\omega^{10}f_{2}+\omega^{15}f_{3}+\omega^{20}f_{4}+\omega^{25}f_{5}+\omega^{30}f_{6}+\omega^{35}f_{7}=x_{5}$$
$$\omega^{0}f_{0}+\omega^{6}f_{1}+\omega^{12}f_{2}+\omega^{18}f_{3}+\omega^{24}f_{4}+\omega^{30}f_{5}+\omega^{36}f_{6}+\omega^{42}f_{7}=x_{6}$$
$$\omega^{0}f_{0}+\omega^{7}f_{1}+\omega^{14}f_{2}+\omega^{21}f_{3}+\omega^{28}f_{4}+\omega^{35}f_{5}+\omega^{42}f_{6}+\omega^{49}f_{7}=x_{7}$$
この連立方程式は,行列表記すると見通しがよい.
$$
\begin{pmatrix}
\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} \\
\omega^{0} &\omega^{1} &\omega^{2} &\omega^{3} &\omega^{4} &\omega^{5} &\omega^{6} &\omega^{7} \\
\omega^{0} &\omega^{2} &\omega^{4} &\omega^{6} &\omega^{8} &\omega^{10} &\omega^{12} &\omega^{14} \\
\omega^{0} &\omega^{3} &\omega^{6} &\omega^{9} &\omega^{12} &\omega^{15} &\omega^{18} &\omega^{21} \\
\omega^{0} &\omega^{4} &\omega^{8} &\omega^{12} &\omega^{16} &\omega^{20} &\omega^{24} &\omega^{28} \\
\omega^{0} &\omega^{5} &\omega^{10} &\omega^{15} &\omega^{20} &\omega^{25} &\omega^{30} &\omega^{35} \\
\omega^{0} &\omega^{6} &\omega^{12} &\omega^{18} &\omega^{24} &\omega^{30} &\omega^{36} &\omega^{42} \\
\omega^{0} &\omega^{7} &\omega^{14} &\omega^{21} &\omega^{28} &\omega^{35} &\omega^{42} &\omega^{49}
\end{pmatrix}
\begin{pmatrix}
f_{0} \\
f_{1} \\
f_{2} \\
f_{3} \\
f_{4} \\
f_{5} \\
f_{6} \\
f_{7}
\end{pmatrix}
=
\begin{pmatrix}
x_{0} \\
x_{1} \\
x_{2} \\
x_{3} \\
x_{4} \\
x_{5} \\
x_{6} \\
x_{7}
\end{pmatrix}
\tag{6}$$
これは,\(f_{0}\sim{f}_{7}\)から\(x_{0}\sim{x}_{7}\)に逆変換している離散フーリエ逆変換の式である.この行列の逆行列が求まれば,\(x_{0}\sim{x}_{7}\)から\(f_{0}\sim{f}_{7}\)に変換する離散フーリエ変換の式が得られる.実はこの行列の逆行列は,行列の各要素を複素共役にして\(8\)で割ることで求まる.まず複素共役を作りたければ\(\omega\)の指数の符号をマイナスにしてやればよい.なぜなら,\(N\)点の離散フーリエ変換において\(\omega\)は\(N\)乗根であり,このケースでは\(8\)乗根であることにより,\(\left|\omega\right|=1\)が言えるからである.つまり,上記式(6)の行列の逆行列は,
$$\frac{1}{8}
\begin{pmatrix}
\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} \\
\omega^{0} &\omega^{-1} &\omega^{-2} &\omega^{-3} &\omega^{-4} &\omega^{-5} &\omega^{-6} &\omega^{-7} \\
\omega^{0} &\omega^{-2} &\omega^{-4} &\omega^{-6} &\omega^{-8} &\omega^{-10} &\omega^{-12} &\omega^{-14} \\
\omega^{0} &\omega^{-3} &\omega^{-6} &\omega^{-9} &\omega^{-12} &\omega^{-15} &\omega^{-18} &\omega^{-21} \\
\omega^{0} &\omega^{-4} &\omega^{-8} &\omega^{-12} &\omega^{-16} &\omega^{-20} &\omega^{-24} &\omega^{-28} \\
\omega^{0} &\omega^{-5} &\omega^{-10} &\omega^{-15} &\omega^{-20} &\omega^{-25} &\omega^{-30} &\omega^{-35} \\
\omega^{0} &\omega^{-6} &\omega^{-12} &\omega^{-18} &\omega^{-24} &\omega^{-30} &\omega^{-36} &\omega^{-42} \\
\omega^{0} &\omega^{-7} &\omega^{-14} &\omega^{-21} &\omega^{-28} &\omega^{-35} &\omega^{-42} &\omega^{-49}
\end{pmatrix}\tag{7}
$$
となるのである.納得が行かない場合は,実際式(6)と式(7)の行列同士を掛け合わせ,丁度単位行列になることを確かめてみるとよいだろう.驚くほど爽快に単純化されるのである.式(6)の両辺に右から行列(7)を掛けると,次のような式が得られる.
$$
\begin{pmatrix}
f_{0} \\
f_{1} \\
f_{2} \\
f_{3} \\
f_{4} \\
f_{5} \\
f_{6} \\
f_{7}
\end{pmatrix}
=
\frac{1}{8} \begin{pmatrix}
\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} &\omega^{0} \\
\omega^{0} &\omega^{-1} &\omega^{-2} &\omega^{-3} &\omega^{-4} &\omega^{-5} &\omega^{-6} &\omega^{-7} \\
\omega^{0} &\omega^{-2} &\omega^{-4} &\omega^{-6} &\omega^{-8} &\omega^{-10} &\omega^{-12} &\omega^{-14} \\
\omega^{0} &\omega^{-3} &\omega^{-6} &\omega^{-9} &\omega^{-12} &\omega^{-15} &\omega^{-18} &\omega^{-21} \\
\omega^{0} &\omega^{-4} &\omega^{-8} &\omega^{-12} &\omega^{-16} &\omega^{-20} &\omega^{-24} &\omega^{-28} \\
\omega^{0} &\omega^{-5} &\omega^{-10} &\omega^{-15} &\omega^{-20} &\omega^{-25} &\omega^{-30} &\omega^{-35} \\
\omega^{0} &\omega^{-6} &\omega^{-12} &\omega^{-18} &\omega^{-24} &\omega^{-30} &\omega^{-36} &\omega^{-42} \\
\omega^{0} &\omega^{-7} &\omega^{-14} &\omega^{-21} &\omega^{-28} &\omega^{-35} &\omega^{-42} &\omega^{-49}
\end{pmatrix}
\begin{pmatrix}
x_{0} \\
x_{1} \\
x_{2} \\
x_{3} \\
x_{4} \\
x_{5} \\
x_{6} \\
x_{7}
\end{pmatrix}
\tag{8}$$
これこそが,\(x_{0}\sim{x}_{7}\)から\(f_{0}\sim{f}_{7}\)に変換する離散フーリエ変換の式となっている.離散フーリエ変換も逆変換も,ともに行列による線形変換であることが明示された.そしてあらゆる\(8\)つの値\(x_{0}\sim{x}_{7}\)について,上記の変換・逆変換は実行できる.もちろんこの\(8\)つの値は複素数でも構わない.つまり,離散フーリエ変換・逆変換は,次の図2に示すように,同じ要素数の(複素)数列同士における線形変換であることがわかった.
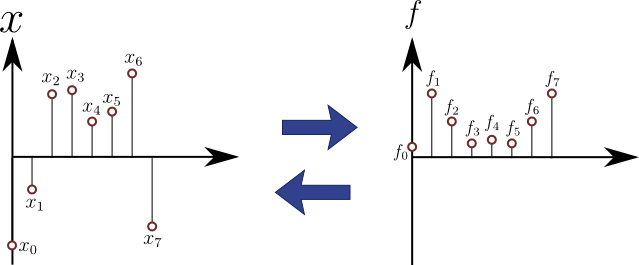
図2.離散フーリエ変換のイメージ1
このように,離散フーリエ変換は離散データ間の線形変換となっている.変換前と変換後の要素数は同じであり,ともに複素数まで扱うことができる.しかしこの変換結果が示す数学的な意味をまだ調べていなかったので,これから3つの具体例について,実際に離散フーリエ変換を実行しながら変換後のデータが示す意味を探っていくことにしよう.まず次の図3が示すのは,基本波をサンプリングしたデータ列の離散フーリエ変換である.
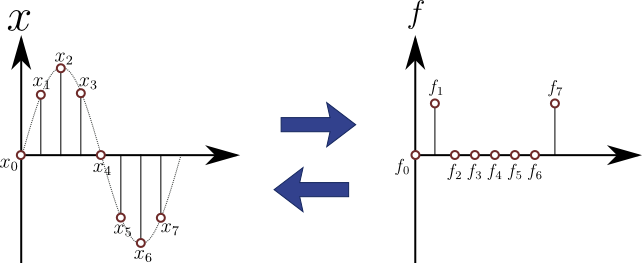
図3.基本波の離散データ列を離散フーリエ変換したとき
図3の変換前データ列\(x_{0}\sim{x}_{7}\)は,サンプリングしている区間がちょうど1周期になるような”基本波”が元になっている離散データ列である.これを離散フーリエ変換すると,同図の右側のように,\(f_{1}\)と\(f_{7}\)だけが\(0\)以外の値をとり,それ以外は\(0\)となる.実は\(f_{1}\)は基本波の成分を表し,\(f_{2}\)は\(2\)次高調波,\(f_{3}\)は\(3\)次高調波の成分をそれぞれ表している.試しに式(8)に\(f_{2}\)だけ\(0\)以外の値を入れたとき\(x_{0}\sim{x}_{7}\)がどうなるかを観察すれば,確かに\(2\)次高調波をサンプリングしたようなデータが出現することからも理解できるだろう.実際\(2\)次高調波の変換は次の図4のようになる.

図4.\(2\)次高調波の離散データ列を離散フーリエ変換したとき
\(2\)次高調波成分のみの離散データ列を変換すると,図4の右側のように\(f_{2}\)と\(f_{6}\)のみが\(0\)以外の値を取るように変換される.ところで\(f_{2}\)が\(0\)以外の値を取ることはわかったが,\(f_{6}\)も値を取るのはなぜなのだろうか?これは\(f_{2}\)の折り返しである.詳しくは書籍等に譲るが,\(f_{6}\)は\(x_{0}\sim{x}_{7}\)が実数であれば丁度\(f_{2}\)の複素共役となる.図3において\(f_{1}\)だけでなく\(f_{7}\)も出現する理由もまた同様である.
それでは最後にエイリアシングのイメージを紹介しよう.上記の図4は\(2\)次高調波の離散フーリエ変換であったが,\(6\)次高調波を同じように離散化しても,図4と同じ結果になることを図5に示した.
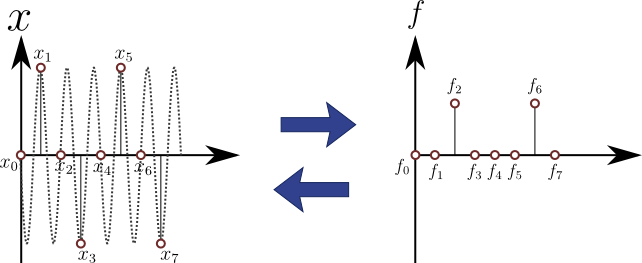
図4.\(6\)次高調波の離散データと\(2\)次高調波の離散データは同じ
サンプリングの仕方次第ではもちろん位相などは異なるものの,\(2\)次高調波をサンプリングしている図4と\(6\)次高調波をサンプリングしている図5は同じである.つまりわずか\(8\)点のサンプリング点数では\(6\)次高調波を扱うことはできず,もしサンプリングしてしまうと\(2\)次高調波と混同してしまうのである.このように扱えないほどの高周波成分が離散化に際して低周波側に折り返される現象をエイリアシングと呼ぶ.\(8\)点のサンプリング点数で扱えるのは\(4\)次高調波までである.逆に\(n\)次高調波まで扱いたければサンプリング点数は\(2n\)点以上にする必要がある.ただしこの制約は離散フーリエ変換の性質ではなく,データを離散化するときの性質である.離散フーリエ変換はいつでも完璧である.\(N\)要素のデータ列を,別の\(N\)要素のデータ列に一対一で変換・逆変換できる.また,データ要素数が\(N=2^{n}\)の形で表されるとき,高速フーリエ変換(FFT)というアルゴリズムを使うことができる.これは離散フーリエ変換が式(6)や式(8)で示すような行列計算であり,\(N\)点離散フーリエ変換の場合は\(N^{2}\)個の要素を計算する必要があるため,例えば\(N\)が400万点必要な解析の場合,計算すべき行列要素の数は16兆個になってしまう.これは如何に高速なマシーンであってもかなりの時間を要する計算である.一方でFFTを用いれば\(N\)点離散フーリエ変換の場合は約\(N\log_{2}{N}\)個の要素を計算すればよく,1億個以内の計算で済む.これは16万倍以上の高速化ということになる.したがってコンピュータ上のフーリエ変換と言えば,ほぼこのFFTのことを指すと思っていただいてよい.
離散フーリエ変換の概要説明は以上である.








 同機機のベクトル図(入門編)
同機機のベクトル図(入門編)


