フーリエ解析の登場
今や現代科学においてなくてはならない数学的道具の一つにフーリエ解析がある.本記事では,このフーリエ解析が如何にして生まれたのか,その歴史も紐解きながら,フーリエ解析とは何なのかといった入門的な疑問にも同時に答えていきたい.
まず,フーリエ解析とはどういったものなのか,次の図1にその数学的イメージを簡単に示してみた.

図1.フーリエ級数展開の数学的イメージ
図1は,フーリエ解析のオリジナルとも言えるフーリエ級数展開のイメージを表している.同図一番上に示されている周期関数は,その周期に等しいサイン波(基本波)と,その整数倍の波数を持ったサイン波(高調波)との重ね合わせに分解できるということを示している.ジョゼフ・フーリエ(1768-1830)は,「ほとんどすべての関数は,サイン波の重ね合わせで表現できる」と主張した.少なくとも普段我々が工学的に扱うような(連続な)関数はすべて,サイン波の足し合わせにより表現でき,すなわちフーリエ級数展開が可能であるという主張である.これは今でこそ現代科学の常識であり,数学的にも証明され,また広く利用されるに至ったわけだが,フーリエが主張していた当時(1810~1820年頃)は数学的な証明もできておらず,また他の数学者からの批判も多かったため一般に広く受け入れられることは無かった.しかしフーリエはこの直感が正しいという強い確信を持ち,この級数展開を自らの研究にも積極的に利用したのである.
それではこのフーリエ解析がどのような場面で役立つのだろうか.実はあらゆる分野で数えきれないほど多くの応用例があり,それだけで分厚い辞典ができるほどの話なのだが,フーリエ解析の原点を知るには,発明者であるフーリエがどのような研究にフーリエ解析(当時はもっぱらフーリエ級数展開)を用いたのか,その歴史を紐解くのがよさそうである.
次の図2は,フーリエが実際にフーリエ級数展開を応用して求めた熱伝導問題のイメージを表している.

図2.温度分布の時間発展(熱伝導)
フーリエは,図2のような熱伝導の時間発展を解析する際に,フーリエ級数展開を用いた.図2の横方向は位置を表し,縦方向は温度を表しているので,これは一次元熱拡散の問題である.温度分布の初期状態は同図の点線で示した矩形波である.つまり,真ん中付近の区間における温度が一様に高く,それ以外の温度は一様に低いという初期状態となる.この温度分布が時間の経過とともにどのようにナラサれるのかを,フーリエ級数展開により求めた.
詳しい熱伝導方程式の導入やその解法は後続の記事に譲るとして,ここでは何故この問題にフーリエ級数展開が有効なのか,そのイメージを簡単に紹介したい.フーリエは,図2における初期値を,次のようにサイン波の足し合わせとして級数展開した.
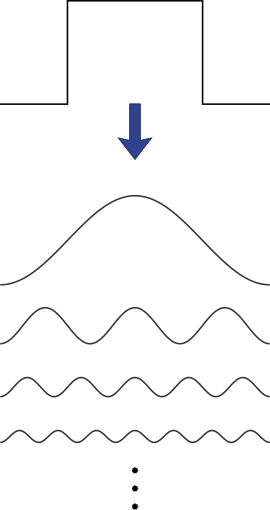
図3.矩形波のフーリエ級数展開
フーリエは図3のように,図2の初期値である矩形波をサイン波の足し合わせとして展開することにより,図2の熱伝導問題を見事に解いた.なぜこの展開が役に立つのか?それは,彼らが扱っていた熱伝導方程式はサイン波の初期値について簡単に解けたからである.また,その方程式は線形だったことも重要である.なぜなら方程式が線形ならば,解の重ね合わせが成り立つからである.つまり,初期値をサイン波に分解したあと,そのぞれぞれのサイン波が初期値だったときの方程式の解を求め,それらをまた重ね合わせることで,任意の初期値のときの方程式の解を求めることができるのである.
フーリエ解析が役立つ場面を簡単にまとめると,次の図4のようになる.

図4.フーリエ解析が役立つ解析対象
いままでの話をまとめると,「1.サイン波で解ける」「2.線形システムである(解の重ね合わせが成り立つ)」という2つの性質を持つ対象を解析するときに,フーリエ級数展開が威力を発揮するということがわかった.
この制約はかなりきついと思われる初学者は多いかもしれない.しかし,我々の身の回りで扱われ,また利用されている工学的システムの多くは図4で表されるような特徴をもつものばかりなのである.簡単に言ってしまえば「入力にサイン波を入れたとき,出力もサイン波か?」という質問と,「入力を\(\alpha\)倍にすると,出力も\(\alpha\)倍になるか?」という質問の2つにYesならば,フーリエ解析は強力に働いてくれる.もちろんこの条件を満たしていなくても,フーリエ変換が役立つ例は沢山あるが,逆に少なくとも上記を満たしていてフーリエ解析が何の役にも立たないという状況は考えにくい.
今はフーリエ解析と言えば,フーリエ級数展開だけでなくフーリエ変換,離散フーリエ変換なども指す.これらはみな兄弟であり,数学的に密接な関係がある.この辺りはおいおい説明するとして,次の記事においては,そもそも本当に「ほとんどすべての関数は,サイン波の重ね合わせで表現できる」のか,その数学的イメージを膨らませよう.
Copyright © 2015 EnergyChord. All rights reserved.



 同機機のベクトル図(入門編)
同機機のベクトル図(入門編)


