フーリエ級数展開はなぜ成り立つのか

 

 

　フーリエは「ほとんどすべての関数は，サイン波の足し合わせで表現できる」と主張し，フーリエ級数展開を誕生させた．本記事では，連続な関数ならば確かにサイン波の足し合わせとして表現できるという明確なイメージを構築していきたい．その絵が頭に浮かぶようになれば，フーリエ級数展開をもっと身近でかつ確からしいものとして扱うことができるようになるだろう．

　まず，フーリエ級数展開のイメージを次の図1でおさらいしてみよう．

 

 

 

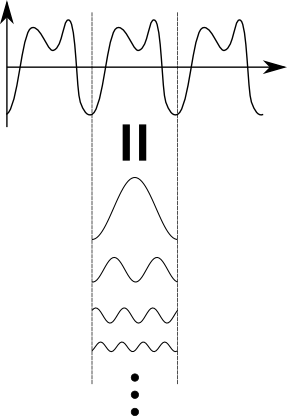
図1.フーリエ級数展開のイメージ

 

 

　図1が示していることは，周期関数ならば，その周期に等しいサイン波（基本波）と，その整数倍の周波数のサイン波（高調波）との重ね合わせとして表現できるというイメージである．本当にそんなことができるのだろうか？どんな関数でもサイン波の和に展開（フーリエ級数展開）できるのか？

　その疑問に答える一つのイメージを紹介しよう．図2を見ていただきたい．

 

 

 

図2.周期関数をある時間間隔でサンプリング

 

 

　図2は図1と同じ周期関数について，ある一定間隔でサンプリングを行った図である．サンプリングされた点の数は1周期あたり\(8\)点ある．ここで数学的には，\(8\)つの”独立”な関数を持ってきて，この\(8\)つの関数の振幅を適当に調整して足し合わせてやれば，少なくともこの\(8\)つの点を同時に通る関数を作ることができることはなんとなく納得がいくだろう．そしてこの\(8\)つの"独立"な関数として，例えば次のような\(8\)つの関数を選ぶことができる．

$$1\tag{1}$$
$$\cos{\frac{2\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\pi{x}}{L}}\tag{2}$$
$$\cos{\frac{2\cdot{2}\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\cdot{2}\pi{x}}{L}}\tag{3}$$
$$\cos{\frac{2\cdot{3}\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\cdot{3}\pi{x}}{L}}\tag{4}$$
$$\cos{\frac{2\cdot{4}\pi{x}}{L}}\tag{5}$$

 

　まず式(1)は定数であり，式(2)は図2の周期関数と同じ周期を持つコサイン関数とサイン関数（基本波），また式(3)は図2の周期関数の周期に\(2\)周期が収まるようなコサイン関数とサイン関数である（\(2\)次高調波）．そして式(4)は図2の周期関数の周期に\(3\)周期が収まるようなコサイン関数とサイン関数であり（\(3\)次高調波），最後の式(5)は図2の周期関数の周期に\(4\)周期が収まるようなコサイン関数となっている（\(4\)次高調波）．

これらの関数が”独立”であることの数学的な説明はあとの記事に譲るとして，とりあえずこれら\(8\)つの関数をうまく振幅調整しながら重ねることで，図2でサンプリングされた\(8\)つの点を同時に通過するような周期関数を合成できるのである！！

つまり，

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{3}\left[a_{n}\cos{\frac{2n\pi{x}}{L}}+b_{n}\sin{\frac{2n\pi{x}}{L}}\right]+a_{4}\cos{\frac{2\cdot{4}\pi{x}}{L}} \tag{6}$$

という式(1)から式(5)までの，合計\(8\)本の関数を重ね合わせるときの係数である\(a_{0}\sim{a}_{4}\)と\(b_{1}\sim{b}_{3}\)（これも合計\(8\)つ）を調節してやれば，図2の\(8\)点をすべて通るような周期関数を必ず用意することができるのである．

　実際図2のサンプリングされた\(8\)点を通過するように式(6)の係数を調節したグラフが次の図3である．

 

 

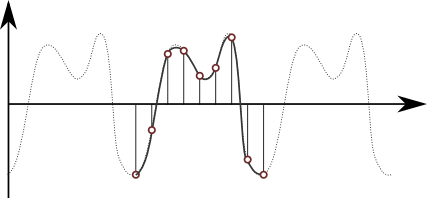
図3.式(6)の\(8\)つの係数を調節して得られた近似曲線（太線）と元の関数（点線）

 

 

　図3において，式(6)の\(8\)つの係数を調節して得られた近似曲線（太線）は，元々の周期関数（点線）をかなりよく近似していることがわかるだろう．これくらい滑らかな関数（ギザギザしていない関数）ならば，三角関数を数個足しただけでもターゲットの関数に相当近い関数を合成できる．もしここで，この図3の元々の関数（点線）に\(4\)次高調波よりも高い周波数の成分が全く入っていなかったとすると，同図の点線と太線は完全に一致する．つまり，1周期分からわずか\(8\)点だけ抽出することで全体を完全に再現できることになる！！これは通信などの世界において無くてはならない超基本性質であり，標本化定理と呼ばれている．ローパスフィルターなどにより高周波が十分に取り除かれた滑らかな波形であれば，わずかなサンプリング点数で波形全体を完全に修復することができるのである．

　それでは次に，もっとギザギザな周期関数をサイン波の足し合わせで表現することを考えてみよう．図4をご覧いただきたい．

 

 

 

図4.もっとギザギザした周期関数とそのサンプリング

 

 

　ギザギザと短い区間でせわしなく値が変化する関数は，それだけ細かい間隔でサンプリングを行わなければ，まともなフィッティングカーブを描くことができないことは明らかである．よって図4においては1周期あたり\(16\)点のサンプリングを行った．先ほどと同様に次のような\(16\)本の関数を用意する．

 

$$1$$
$$\cos{\frac{2\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\pi{x}}{L}}$$
$$\cos{\frac{2\cdot{2}\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\cdot{2}\pi{x}}{L}}$$
$$\cos{\frac{2\cdot{3}\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\cdot{3}\pi{x}}{L}}$$
$$\cdot\cdot\cdot$$
$$\cos{\frac{2\cdot{7}\pi{x}}{L}}{,}\,\,\,\,\sin{\frac{2\cdot{7}\pi{x}}{L}}$$
$$\cos{\frac{2\cdot{8}\pi{x}}{L}}$$

 

 

これら\(16\)本の関数をうまく振幅調整しながら重ねることで，図4でサンプリングされた\(16\)個の点を同時に通過するような周期関数を合成できる．

つまり，

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{7}\left[a_{n}\cos{\frac{2n\pi{x}}{L}}+b_{n}\sin{\frac{2n\pi{x}}{L}}\right]+a_{8}\cos{\frac{2\cdot{8}\pi{x}}{L}} \tag{7}$$

合計\(16\)本の関数を重ね合わせるときの係数である\(a_{0}\sim{a}_{8}\)と\(b_{1}\sim{b}_{7}\)（これも合計\(16\)個）を調節してやれば，図4の\(16\)点をすべて通るような周期関数を必ず用意することができる．

　実際図4のサンプリングされた\(16\)点を通過するように式(7)の係数を調節したグラフが次の図5である．

 

 

 

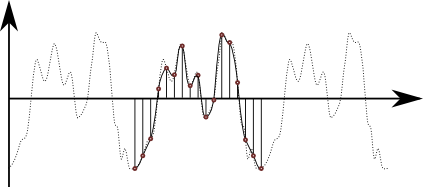
図5.式(7)の\(16\)個の係数を調節して得られた近似曲線（太線）と元の関数（点線）

 

 

　今回の周期関数は少しギザギザ過ぎた（高周波成分が多すぎた）ので，\(16\)点のサンプリング点を使ってもまだ太線と点線との間に若干の乖離がみられる．しかしこの違いは，さらに点数を\(32\)点，\(64\)点，，，と増やしていくことで，どんどん小さくなることは明らかであろう．つまり言い換えると，非常に高周波なサイン波まで際限なく足し合わせていけば，いつかはその元々の周期関数へと収束していくことが可能なのである．

　そうすると，連続な任意の関数\(f\left({x}\right)\left({0}\leq{x}\leq{L}\right)\)は，次のようにサイン・コサイン関数の級数として展開できることが自然と理解できるだろう．

$$f\left({x}\right)=a_{0}+\sum_{n=1}^{\infty}\left[a_{n}\cos\left(\frac{2n\pi}{L}x\right)+b_{n}\sin\left(\frac{2n\pi}{L}x\right)\right] \tag{8}$$

 

　上記式(8)の\(\Sigma\)内の\(\sin{,}\cos\)はすべて，\(x\)軸に対して\(L\)だけ平行移動しても値は変わらないので，式(8)自体が周期\(L\)の周期関数になっていることがわかる．つまり，関数\(f\left({x}\right)\left({0}\leq{x}\leq{L}\right)\)が，\(x\geq{L}\)においても周期\(L\)で繰り返される形となる．このように，ある区間で連続な任意の関数は，その区間においてサイン波の重ね合わせとして級数展開でき，これをフーリエ級数展開と呼んでいる．

　次の記事は，上記のイメージにおいても重要な役割を果たした離散フーリエ変換について，簡単な数学的イメージを紹介しよう．離散フーリエ変換に興味がなく，フーリエ級数展開のまとめに進みたい方は，そのもう一つ先の記事に直接進んでもらって構わない．